Iterative solvers are used in equations when reordering methods for direct solvers are not efficient and the stiffness matrix K is sufficiently well-conditioned.
Generalities
Iterative solvers are recommended for well-conditioned large-scale problems(15,000 - 1,000,000 equations), linear static tasks, and eigenvalue problems (modal or buckling analysis).
The traditional direct methods, that is, the Frontal, Skyline, and Sparse methods, are time-consuming and require large amounts of disk space to store a factorized matrix.
Iterative solvers, on the other hand, considerably reduce the computation time and disk storage requirements. However, they have certain disadvantages:
- They converged slowly when poorly conditioned problems are met.
- Each load case is computed iteratively from the beginning. Load cases should be defined as few as possible.
Iterative solvers are efficient for the analysis of structures containing solid FE. They are also useful during linear static analyses (searching for optimal design parameters, for example), when it is possible to obtain approximate solutions for a few load cases.
The element-by-element control of the data correctness of Vinget regularization constitutes an additional application of iterative solvers which enables you to detect difficulties finding errors in the FE model.
The preconditioned gradient method (PCG) includes several types of preconditioning.
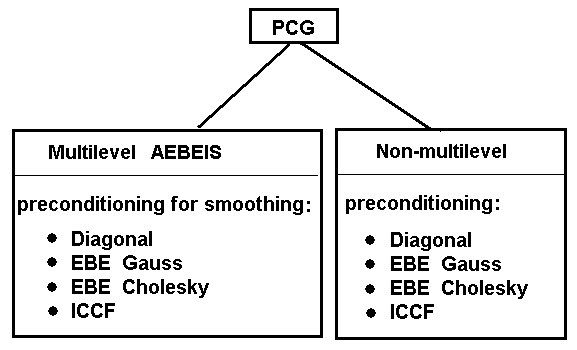
- AEBEIS: Aggregation Element-by-Element Iterative Solver 1,2 .
- EBE: Element-by-Element.
- ICCF: Incomplete Cholesky Factorization approach.
Element-by-element (PCGEBE) and multilevel iterative solver (AEBEIS)
The element-by-element solver (PCGEBE) is used for all types of finite elements and not limited by the size of the problem. However, it is sensitive to poor conditioning of the stiffness matrix K - possible slow convergence.
The multilevel iterative solver (AEBEIS) is a multilevel, aggregation, element-by-element iterative solver that combines the advantages of quick iterative methods with the inexpensive EBE technique. It allows the acceleration of basic operations by means of the inexpensive method regarding memory requirements. Aggregation methods such as this allow analysis of solids and shells (just as multigrid methods do), as well as bars and combination structures from bars, shells, and solids.
The AEBEIS solver typically provides quicker convergence compared to non-multilevel methods. It ensures a stable convergence for poorly conditioned problems, but it is less safe. In rare cases the preconditioning is locked, whereas the convergence is still slow. This solver was implemented by combining the aggregation solver based on the EBE technique.
The AEBEIS solver enables the application of 2D and 3D bar elements, shell elements (3, 4, 6, and 8 node elements), solid elements. It also enables additional structure component elements such as elastic supports, offsets, releases, and rigid links. There are no restrictions concerning element or structure types for a non-multilevel method.
The following types of preconditioning are available in both AEBEIS and non-multilevel methods.
- Diagonal - Jacobi preconditioning (apply only in well-conditioned problems).
- EBE Gauss - modified EBE Gauss-Seidel-Cholesky preconditioning 12.
- EBE Cholesky - EBE Cholesky preconditioning 34.
- ICCF - incomplete Cholesky factorization approach 56.
The ICCF approach is quicker than other methods (Diagonal, EBE Gauss, EBE Cholesky) and uses approximately the same number of iterations to obtain convergence, such as the EBE Gauss or EBE Cholesky methods. It does not use the I/O operations of the disk but maintains higher RAM requirements. ICCF is preferred if the computer has enough RAM for the task. RAM and disk requirements of EBE Gauss and EBE Cholesky methods are minimal, but they are slower than the ICCF approach.