초탄성

이 재질 유형은 Explicit 해석에서 지원되지 않습니다. 아이소파라메트릭 솔리드 요소에 대해 고무 같은 재료(탄성중합체)의 완전 비선형(큰 변형 및 큰 회전) 초탄성 해석에서 사용할 재료 특성을 정의합니다.

• 일반화된 Mooney-Rivlin 변형 에너지는 다음과 같이 표현할 수 있습니다.

  

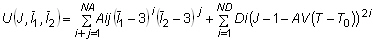
  여기서 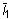및 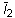는 각각 첫 번째와 두 번째 왜곡 변형 불변입니다. J = det F는 변형 구배의 행렬식입니다. 작은 변형에서 2D1 = K이고 2(A10 + A01) = G이며 K는 벌크 계수입니다. NA = 1인 경우 모델이 Mooney-Rivlin 재료로 감소하고 NA = 1이고 A01 = 0.0인 경우 Neo-Hookean 재료로 감소합니다. Neo-Hookean 또는 Mooney-Rivlin 재료의 경우 연속 항목이 필요하지 않습니다. 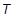는 현재 온도이고 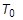은 초기 온도입니다.

• 일반화된 Ogden 변형 에너지는 다음과 같이 표현될 수 있습니다.

  

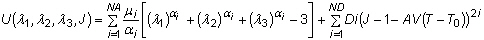
  여기서 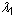, 및 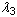은 주 신축입니다. J = det F는 변형 구배의 행렬식입니다. 작은 변형에서 2D1 = K이며 K는 벌크 계수입니다. 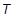는 현재 온도이고 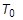은 초기 온도입니다.

  D1의 기본값은 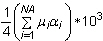입니다. D2 - D4의 기본값은 0입니다.

• 초탄성 재료는 완전 비압축 또는 거의 비압축 동작을 나타냅니다. 완전 비압축은 현재 사용할 수 없는 반면 거의 비압축 동작은 큰 D1 값을 사용하여 시뮬레이션할 수 있습니다.

유형 드롭다운에서 초탄성을 선택하면 초탄성, 실험 데이터 함수 및 Mullins 계수 재료 섹션을 사용할 수 있습니다.

• 초탄성

  

  

  

  

  

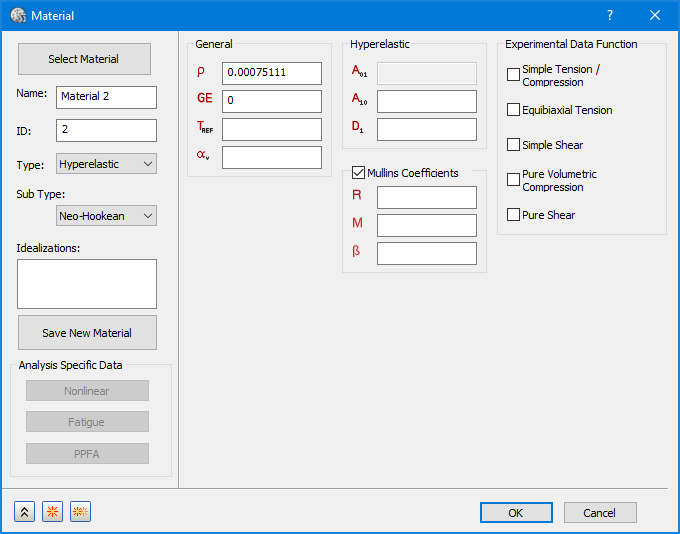
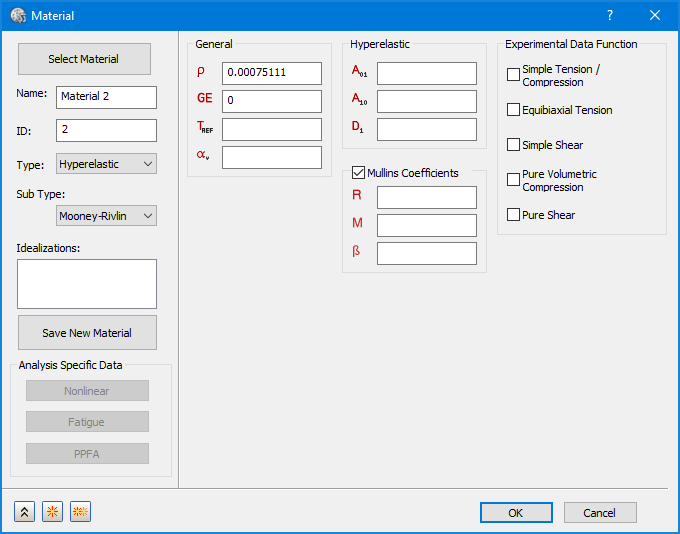
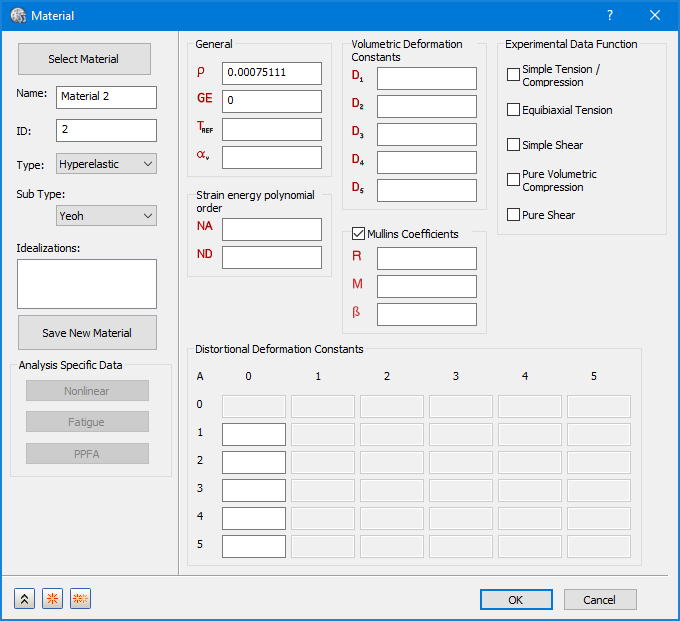
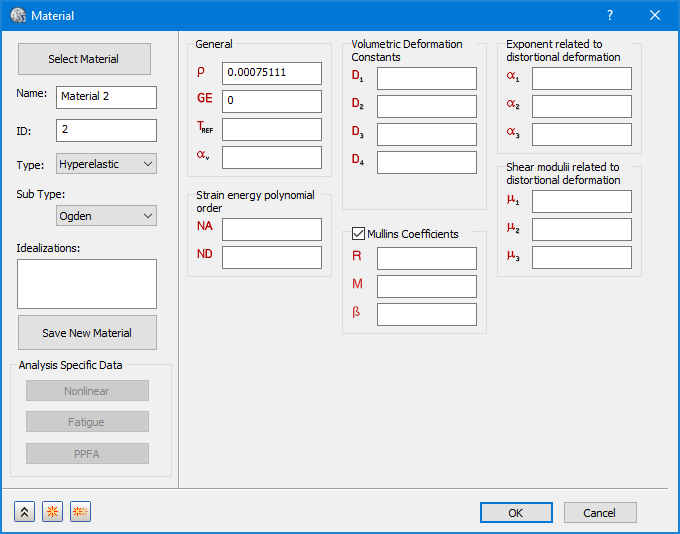
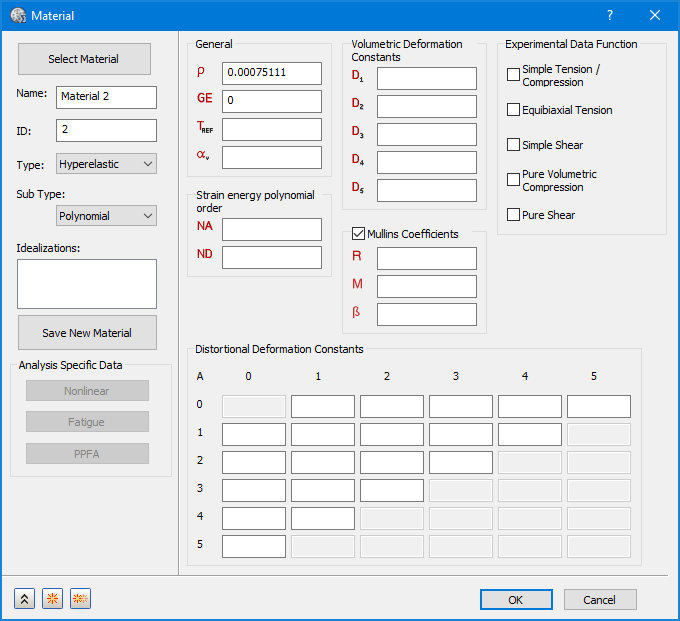
  • 하위 유형의 경우 위의 이미지에 표시된 대로 Neo-Hookean, Mooney-Rivlin, Ogden, Yeoh 및 다항식을 선택할 수 있습니다. 각 유형에는 정의할 특정 재료 상수 세트가 있습니다.
  • 모든 구조 요소에 대한 질량을 자동 계산하기 위해 질량 밀도, RHO가 사용됩니다.
  • 댐핑 계수 GE를 얻으려면 임계 댐핑비 C/C0에 2.0을 곱합니다. 재료 구조 댐핑에 대해 지배적 주파수가 정의되지 않은 경우(댐핑 섹션 참조) 과도 응답 해석에서 GE가 무시됩니다.
  • TREF는 선형 솔루션에서 열 하중 계산을 위한 참조 온도로만 사용됩니다. 초기 온도 하중이 지정되면 TREF가 무시됩니다.
  • 열팽창 계수, 질량 밀도, 재료 댐핑 계수 및 재료 참조 재료를 정의할 수 있습니다.
• 실험 데이터 함수
  • Aij 및 Di는 실험 데이터의 최소 제곱법에서 가져옵니다. Aij를 구하기 위해 4가지 실험(단순 장력 압축, 동 이축 장력, 단순 전단, 순수 전단, 순수 체적 압축) 중 하나 이상을 사용할 수 있습니다. Di는 순수 체적 압축 데이터(TABD)에서 얻을 수 있습니다. TAB1에서 TAB4까지 모두 비어 있으면 Aij는 사용자가 지정해야 합니다. 테이블에서 지정된 매개변수 평가는 매개변수의 수동 입력을 대체합니다.
  • ND = 1이고 0이 아닌 D1 값이 제공되거나 순수 체적 압축의 실험 데이터에서 구하면 재료 상수 Aij의 매개변수 평가는 단순 장력/압축, 동 이축 장력 및 일반 쌍축 변형의 경우 압축률을 고려합니다. 그렇지 않으면 재료 상수 평가에서 완전 비압축이 가정됩니다.

    

    • 테이블 아이콘: 물리적 테스트에서 얻은 실험 데이터 함수를 정의할 수 있습니다. 단순 장력/압축, 동 이축 장력, 단순 전단, 순수 전단 및 순수 체적 압축의 테이블을 정의할 수 있습니다.
    • 단순 장력/압축: 재료 상수 Aij의 평가에서 사용할 데이터입니다. 테이블의 xi 값은 연신률 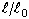이어야 하고, yi 값은 엔지니어링 응력 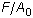의 값이어야 합니다. 응력은 압축의 경우 음수이고 장력의 경우 양수입니다. 이 규칙을 준수하지 않는 경우 솔루션이 수렴하지 못할 수 있습니다.
    • 동 이축 장력: 재료 상수 Aij의 평가에서 사용할 데이터입니다. 테이블의 xi 값은 연신률 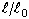이어야 합니다. yi 값은 엔지니어링 응력 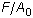의 값이어야 합니다. 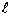는 현재 길이이고, F는 현재 힘이며, 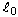는 초기 길이이고 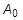은 횡단 영역입니다. 구형 막의 압력의 경우 엔지니어링 응력이 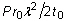에서 제공되며, 여기서 P는 압력의 현재 값이고 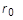및 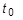은 초기 반지름 및 두께입니다.
    • 단순 전단: 재료 구속조건 Aij의 평가에서 사용할 데이터입니다. 테이블의 xi 값은 전단 접선 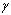의 값이어야 하고 yi 값은 엔지니어링 응력 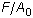의 값이어야 합니다.
    • 순수 전단: 재료 구속조건 Aij의 평가에서 사용할 데이터입니다. 테이블의 xi 및 yi 값은 연신률 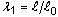및 공칭 응력 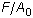의 값이어야 합니다. 1방향에서 각각 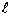는 현재 길이이고, F는 현재 힘이며, 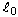및 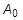은 초기 길이 및 횡단 영역입니다.
    • 순수 체적 압축: 재료 구속조건 Di 평가에서 사용할 데이터입니다. 테이블의 xi 값은 체적 비 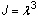의 값이어야 하고 여기서 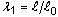은 3방향 모두에서의 연신률입니다. yi 값은 압력 값이어야 하는데 압축에서 양수로 가정됩니다.
• Mulins 계수(Explicit 해석 관련)
  
  • 초탄성 재질에 대한 Mullins 효과를 지정합니다. 이 확인란은 Explicit 해석을 실행하는 경우에만 선택해야 합니다.
  • R, M, β 항목은 Mullins 계수입니다.