하중 변동은 스칼라 표면을 기반으로 합니다. 따라서 3차원 하중 변동을 허용합니다. 변동에는 선형 및 2차 거리 가중치 적용 공식화가 있으므로 분산은 정확히 일치하지 않지만 하중 분산은 매우 가까워질 수 있습니다. 2차/포물선형 거리 가중치 적용 공식화를 사용하면 더 적은 점 데이터를 사용하여 "더 나은" 분산을 제공할 수 있습니다.
고급 옵션 버튼을 클릭하면 하중 양식에서 사용할 수 있습니다.
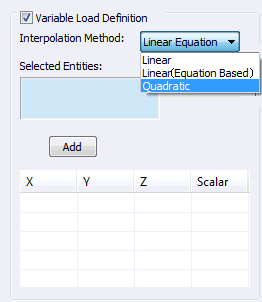
-
보간 방법:
- 선형: 모서리 또는 곡선의 경우 선택한 관련 형상의 두 끝 점 또는 정점을 사용하여 보간합니다. 면의 경우 선형 순서로 하중을 보간하려면 네 개의 점이 필요합니다.
- 선형(방정식 기반): 모서리 또는 곡선의 경우 선택한 관련 형상의 두 끝 점 또는 정점을 사용하여 보간합니다. 면의 경우 표준 평면 방정식을 사용하여 선형 순서로 하중을 보간하려면 세 개의 점이 필요합니다.
- 2차: 모서리 또는 곡선의 경우 선택한 관련 형상의 두 끝 점 또는 정점을 사용하여 보간합니다. 면의 경우 포물선형 순서로 하중을 보간하려면 네 개의 점이 필요합니다.
-
예 1: 편평한 표면의 단순 2D 변동
아래 이미지와 같이 분산된 하중을 적용할 판을 고려합니다.

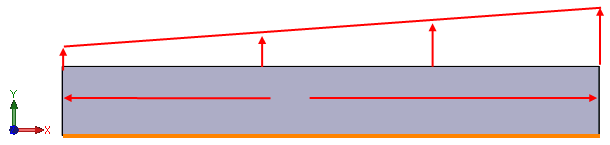
모서리를 따라 단위 하중을 정의합니다.
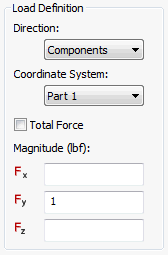
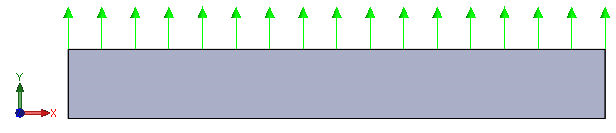
가변 하중 정의 상자를 선택합니다. 점 및 정점을 선택한 도면요소로 사용할 수 있으므로 향후 모델에 대한 가변 하중 분산을 작성할 때 참조 형상을 작성하면 유용할 수 있습니다.
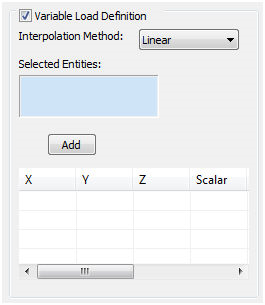
- 보간 방법을 선형으로 설정합니다. 선택한 도면요소 선택 상자를 사용하여 형상의 두 끝 점을 선택합니다. 먼저 클릭하여 활성화할 수 있습니다.
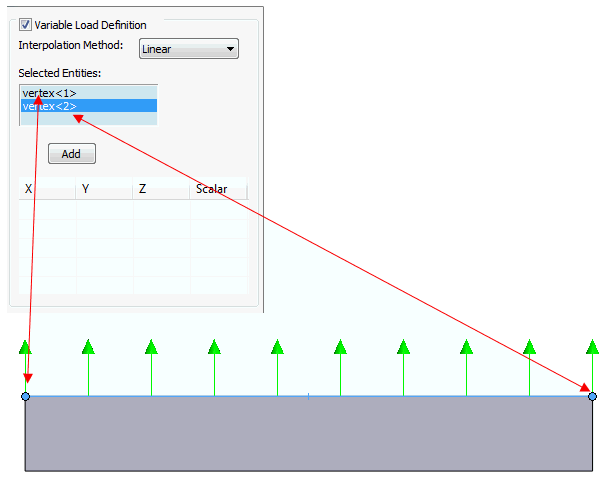
추가 버튼을 클릭하여 테이블에 3차원 위치를 추가합니다.
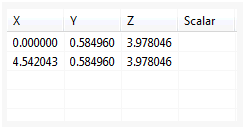
첫 번째 점은 스칼라 값이 0.0이고, 두 번째 점은 스칼라 값이 5.0입니다. 스칼라 상자를 두 번 클릭하여 값을 입력합니다.
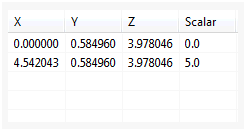
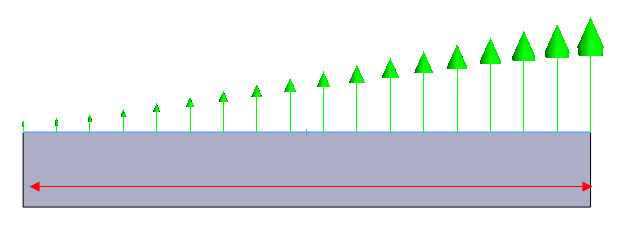
곡선이 완벽한 선형 곡선이 아니라 포물선형인지 확인합니다. 위의 치수를 기반으로 총 하중이 2.5임을 확인할 수 있습니다.
- 이제 보간 방법을 선형(방정식 기반)으로 변경합니다.
표면에서 세 번째 점이 누락되었으므로 하중 화살표를 표시할 수 없습니다. 세 번째 점을 선택하고 리스트에 추가한 다음 아래 이미지와 같이 동일한 5.0 값을 입력합니다.
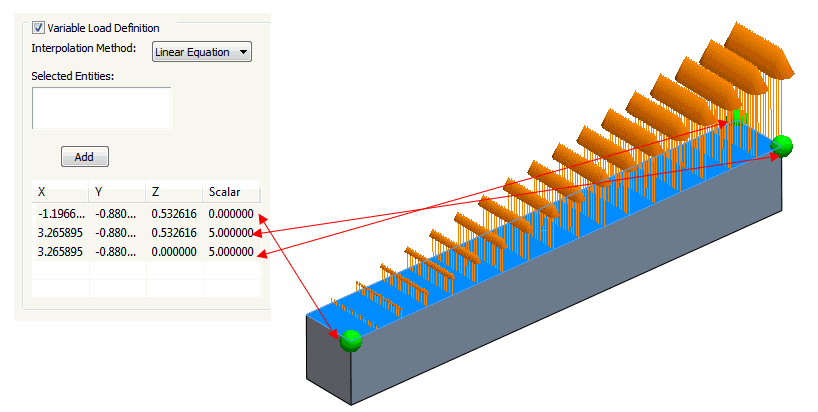
- 이제 보간 방법을 2차로 변경합니다.
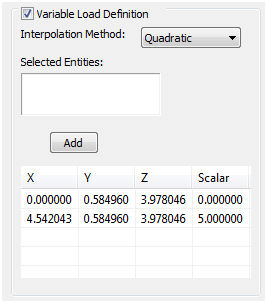
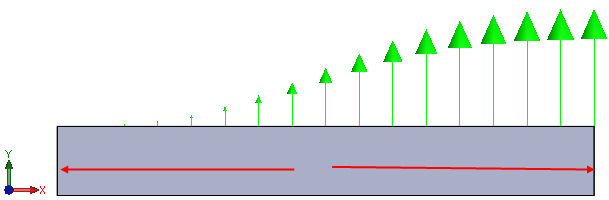
- 보간 방법을 선형으로 설정합니다. 선택한 도면요소 선택 상자를 사용하여 형상의 두 끝 점을 선택합니다. 먼저 클릭하여 활성화할 수 있습니다.
-
예 2: 원통형 표면의 단순 2D 변동
원통형 표면에서 가변 하중(예: 베어링 하중)을 정의하려면 아래 이미지와 같이 선형(방정식 기반)이 아니라 선형 옵션을 사용하는 것이 좋습니다.
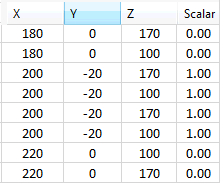
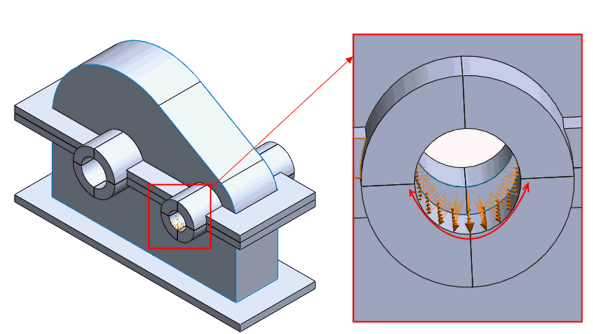
-
예 3: 정수력 하중의 단순 2D 변동
정수력 가변 하중을 정의하려면 아래 이미지와 같이 선형이 아니라 선형(방정식 기반) 옵션을 사용하는 것이 좋습니다.
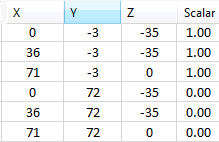
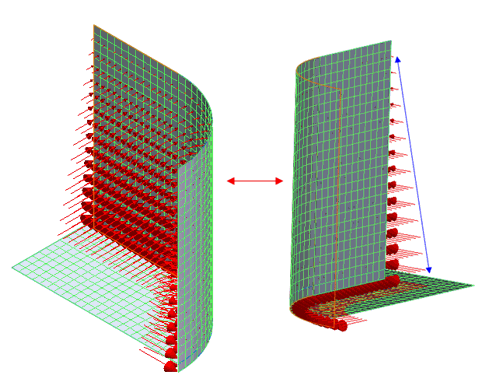
-
예 4: 편평한 표면의 단순 3D 변동
표면에서 동일한 스칼라 표면 점을 사용하여 다음과 같은 하중 분산을 작성합니다. 하중 분산은 데이터 점에서 위치가 멀수록 1.0(단위 값)으로 수평을 유지합니다.
-
선형
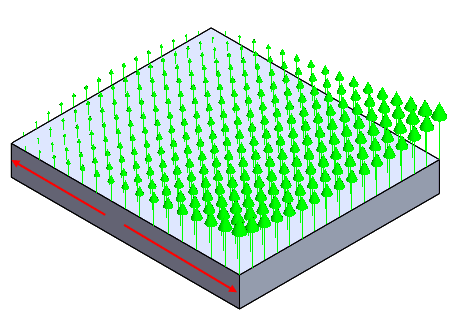
-
2차
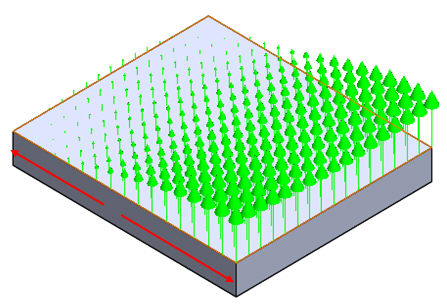
-
선형