ELIPSA (polecenie)

Tworzy elipsę lub łuk eliptyczny.

Wyszukiwanie

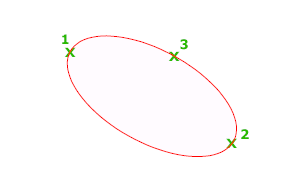
Pierwsze dwa punkty elipsy określają położenie i długość pierwszej osi. Trzeci punkt określa odległość między środkiem elipsy a punktem końcowym drugiej osi.

Wyświetlane są następujące monity.

Punkt końcowy osi

Definiuje pierwszą oś poprzez jej dwa punkty końcowe. Kąt pierwszej osi określa kąt elipsy. Pierwsza oś może definiować zarówno małą jak i wielką oś elipsy.

Odległość od innej osi

Definiuje drugą oś przy użyciu odległości punktu środkowego pierwszej osi do punktu końcowego drugiej osi (3).

Obrót:

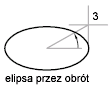
Tworzy elipsę przez obrócenie okręgu względem pierwszej osi.

Przenieś krzyż nitkowy nad środek elipsy i kliknij. Jeśli wprowadzisz wartość, wraz z jej wzrostem wzrośnie niewspółśrodkowość elipsy. Podanie 0 definiuje elipsę kołową.

Łuk

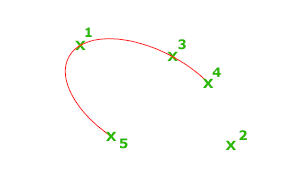
Tworzy łuk eliptyczny.

Kąt pierwszej osi określa kąt łuku eliptycznego. Pierwsza oś może definiować zarówno główną, jak i pomocniczą oś, w zależności od rozmiaru.

Pierwsze dwa punkty łuku eliptycznego określają położenie i długość pierwszej osi. Trzeci punkt określa odległość między środkiem łuku eliptycznego a punktem końcowym drugiej osi. Czwarty i piąty punkt to kąty początkowy i końcowy.

Punkt końcowy osi

Definiuje początek pierwszej osi.

Obrót:

Definiuje stosunek osi elipsy przez obrót okręgu wokół osi głównej. Im większa wartość (od 0 do 89,4 stopnia), tym większa wartość współczynnika określającego stosunek osi pomocniczej do głównej. Wartości z zakresu od 89,4 do 90,6 stopnia są nieprawidłowe, ponieważ elipsa będzie wyglądać jak linia prosta. Użycie wielokrotności tych wartości kątów powoduje tworzenie lustrzanych odbić co 90 stopni.

Kąt początkowy

Definiuje pierwszy punkt końcowy łuku eliptycznego. Opcja Kąt początkowy zmienia również tryb Parametr na Kąt. Tryb steruje obliczaniem elipsy.

Parametr (opcja specjalistyczna)

Wymaga wprowadzenia kątowego, ale tworzy łuk eliptyczny przy użyciu poniższego równania wektora parametru dla kąta każdego punktu końcowego:

p(kąt) = c + a * cos(kąt) + b * sin(kąt)

gdzie c to środek elipsy, a a i b to jej główne i poboczne osie.

• Parametr końcowy: Definiuje końcowy kąt łuku eliptycznego przy użyciu równania wektorów parametrów. Opcja Parametr początkowy przełącza z trybu Kąt na Parametr. Tryb steruje obliczaniem elipsy.
• Kąt:Definiuje kąt końcowy łuku eliptycznego. Opcja Kąt początkowy przełącza z trybu Parametr na tryb Kąt początkowy. Tryb steruje obliczaniem elipsy.
• Kąt rozwarcia: Definiuje kąt rozwarcia rozpoczynający się w kącie początkowym.

Środek

Tworzy elipsę przy użyciu środka, punktu końcowego pierwszej osi oraz długości drugiej osi. Można określić odległości, klikając lokalizację w odpowiedniej odległości lub wprowadzając wartość długości.

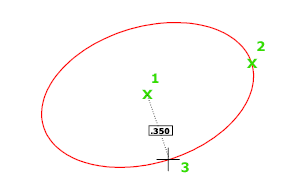
Odległość od innej osi

Definiuje drugą oś jako odległość od środka elipsy lub punktu środkowego pierwszej osi do określonego punktu.

Obrót:

Tworzy elipsę przez obrócenie okręgu względem pierwszej osi.

Przenieś krzyż nitkowy nad środek elipsy i kliknij. Jeśli wprowadzisz wartość, wraz z jej wzrostem wzrośnie niewspółśrodkowość elipsy. Wprowadzenie 0 tworzy okrąg.

Izo

Tworzy okrąg izometryczny w bieżącej płaszczyźnie izometrii.

Uwaga: Opcja Izo (okrąg izometryczny) jest dostępna tylko wtedy, gdy opcja IZOSZKIC2D ma wartość Izo (płaszczyzna izometryczna) lub opcja Styl polecenia SKOK ma wartość Izometryczny.

Promień

Tworzy izometryczną reprezentację okręgu, wykorzystując podany promień.

śreDnica

Tworzy izometryczną reprezentację okręgu, wykorzystując podaną średnicę.