Funkcja nor oblicza jednostkowy wektor normalny (wektor prostopadły do linii lub płaszczyzny). Wektor definiuje kierunek normalny, a nie położenie w przestrzeni (nie jest to punkt). Aby uzyskać inny punkt można dodać ten wektor normalny do punktu.
- nor
-
Określa jednostkowy normalny wektor 3D wybranego okręgu, łuku lub łukowego segmentu polilinii. Ten wektor normalny jest współrzędną Z układu współrzędnych obiektu (UWO) wybranego obiektu.
- nor(v)
-
Określa jednostkowy normalny wektor 2D względem wektora v. Obydwa wektory są traktowane jako rzut 2D na płaszczyznę XY bieżącego układu LUW. Zwrot uzyskanego wektora normalnego jest taki, że wskazuje on na lewo od oryginalnego wektora v.
- nor(p1,p2)
-
Określa wektor jednostkowy 2D normalny względem linii p1,p2. Linia jest skierowana od punktu p1 do p2. Zwrot uzyskanego wektora normalnego jest taki, że wskazuje on na lewo od oryginalnej linii (p1,p2).
- nor(p1,p2,p3)
-
Określa wektor jednostkowy 3D normalny względem płaszczyzny zdefiniowanej przez trzy punkty p1, p2 oraz p3. Zwrot uzyskanego wektora normalnego jest taki, że dane punkty biegną w kierunku przeciwnym do ruchu wskazówek zegara w stosunku do normalnej.
Poniższe ilustracje pokazują sposób wyznaczania wektorów normalnych:
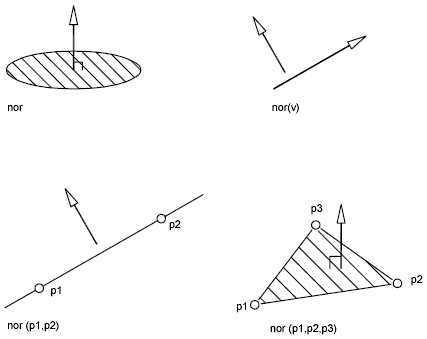
Kolejny przykład ustala kierunek obserwacji prostopadły do wybranego obiektu. Obiekt ten jest wyświetlany w widoku planu i rzut równoległy go nie zniekształca.
Polecenie: pktobs
Bieżący kierunek widoku: KIEROBS=bieżący
Określ punkt widoku lub [Obróć] <wyświetl kompas i trójnóg>: 'kalk
>> Wyrażenie: nor
>> Wybierz okrąg, łuk lub polilinię dla funkcji NOR: