Aby uzyskać więcej informacji, zobacz temat Definiowanie sumowań tolerancji.
Podstawowe równania dla zamkniętych łańcuchów wymiarów liniowych można wyprowadzić z poniższej ilustracji.
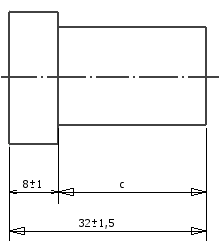
a = 32 ± 1,5 mm, b = 8 ± 1 mm
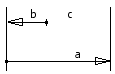
Zwiększanie/zmniejszanie elementów
Jeżeli element narastający rośnie, element zamykający także rośnie. Jeśli element malejący rośnie, element zamykający maleje, jeśli inne elementy łańcucha pozostają stałe.
|
Element zamykający: |
1. c = a - b |
|
Górny wymiar graniczny zamykającego elementu: |
2.c max = a max - b min |
|
Dolny wymiar graniczny zamykającego elementu: |
3.c min = a min - b max |
|
Tolerancja elementu zamykającego (odjęcie równania 3 od równania 2) |
4. c max - c min = a max - a min - (b min - b max ) |
|
Tak jak |
5. T c = T a + T b |
Na ogół tolerancje łańcucha liniowego spełniają poniższe równanie.
![]()
Podobnie równania 2 i 3 można zapisać w ogólnej postaci.
![]()
![]()
Górny wymiar graniczny elementu zamykającego równy jest różnicy sumy górnych wymiarów granicznych powiększanych elementów i sumy dolnych wymiarów granicznych elementów zmniejszanych.
Dolny wymiar graniczny elementu zamykającego równy jest różnicy sumy dolnych wymiarów granicznych powiększanych elementów i sumy górnych wymiarów granicznych elementów zmniejszanych.
Wymiar nominalny elementu zamykającego można wyrazić używając równania 1, jak w poniższym równaniu.
![]()
Górna granica odchyłki elementu zamykającego:
![]()
Dolna granica odchyłki elementu zamykającego:
![]()