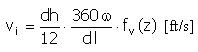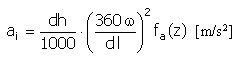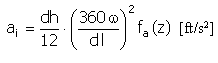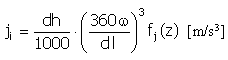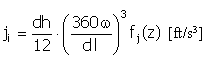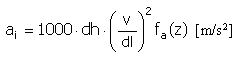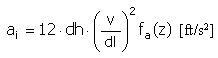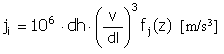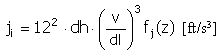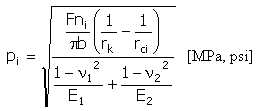Dane wejściowe:
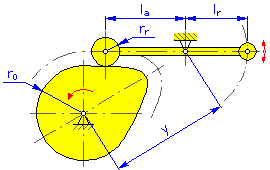
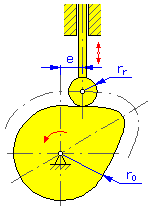
- Promień bazowy r 0 (krzywki dyskowe i walcowe)
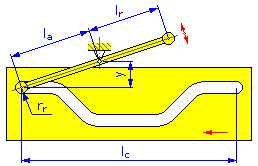
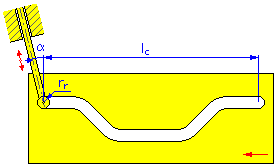
- Długość ruchu l c (krzywki liniowe)
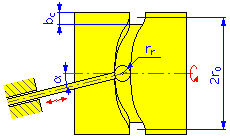
- Szerokość krzywki b c
- Promień rolki r r
- Szerokość rolki b r (dla walca kształtu popychacza)
- Mimośrodowość e (krzywki dyskowe popychacza przesuwnego)
- Kąt mimośrodowości α (krzywki liniowe i walcowe popychacza przesuwnego)
- Odległość punktu podparcia (krzywki liniowe i dyskowe wahacza poprzecznego)
- Długość wahacza l a (krzywki dyskowe i liniowe wahacza poprzecznego)
- Ramię reakcyjne l r (krzywki dyskowe i liniowe wahacza poprzecznego)
- Prędkość ω (krzywki dyskowe i walcowe)
- Szybkość v (krzywki liniowe)
- Siła na rolce F
- Waga przyśpieszona m
- Sztywność sprężyny c
- Dopuszczalny nacisk p A1
- Moduł sprężystości materiału krzywki E 1
- Współczynnik Poissona materiału krzywki μ 1
- Dopuszczalny nacisk p A2
- Moduł sprężystości materiału popychacza E 2
- Współczynnik Poissona materiału popychacza μ 2
|
Krzywka tarczowa |
|
|
|
|
|
Krzywka liniowa |
|
|
|
|
|
Krzywka walcowa |
|
 |
|
|
Średnica zewnętrzna = 2r 0 + b c |
|
|
Średnica wewnętrzna = 2r 0 - b c |
|
Segmenty krzywki
- Funkcja ruchu f y (z) [ul]
- Współczynnik odwrotności k r (tylko dla ruchów parabolicznego i parabolicznego z częścią liniową)
- Część liniowa k l (tylko dla ruchu parabolicznego z częścią liniową)
- Pozycja na początku ruchu l 0 [°; mm, cal]
- Pozycja na końcu ruchu l [°; mm, cal]
- Długość segmentu w trakcie ruchu dl = l - l 0 [°; mm, cal]
- Skok na początku h 0 [mm, cal]
- Skok na końcu h max [mm, cal]
- Skok segmentu d h = h max — h 0 [mm, cal]
Zależności skoku
Krzywka dyskowa i walcowa
Kąt obrotu krzywki ϕ i [°]
Rzeczywista pozycja względna w segmencie: z i = (ϕ i - l 0 ) / dl (zakres 0 - 1)
|
Skok |
y i = dh f y (z) [mm, in] |
|
Prędkość |
|
|
|
|
|
Przyspieszenie |
|
|
|
|
|
Puls |
|
|
|
Krzywka liniowa
Pozycja krzywki podczas ruchu l i [mm, cal]
Rzeczywista pozycja względna w segmencie: z i = (l i - l 0 ) / dl (zakres 0 - 1)
|
Skok |
y i = dh f y (z) [mm, in] |
|
Prędkość |
|
|
Przyspieszenie |
|
|
|
|
|
Puls |
|
|
|
Funkcje ruchu
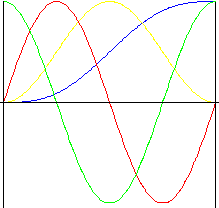
Cykloida (przedłużona sinusoida)
Ruch ten wykazuje doskonałe charakterystyki przyspieszenia. Jest często stosowany dla krzywek o szybkich obrotach, ponieważ charakteryzuje się niskim poziomem hałasu, drgań i zużycia.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Skok |
f y (z) = z - 0,5/π sin(2πz) |
|
Prędkość |
f v (z) = 1 - cos (2πz) |
|
Przyspieszenie |
f a (z) = 2π sin(2πz) |
|
Puls |
f j (z) = 4π 2 cos(2πz) |
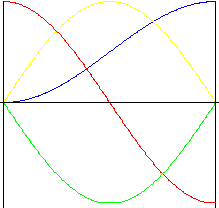
Harmoniczny (sinusoidalny)
Płynna zmiana prędkości i przyspieszanie podczas skoku są naturalnymi zaletami takiej krzywej. Jednakże chwilowe zmiany przyspieszenia na początku i przy końcu ruchu mogą prowadzić do drgań, hałasu i zużycia.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Skok |
f y (z) = 0,5 (1 - cos πz)) |
|
Prędkość |
f v (z) = 0,5 π sin (πz) |
|
Przyspieszenie |
f a (z) = 0,5 π 2 cos(πz) |
|
Puls |
f j (z) = -0,5π 3 sin(πz) |
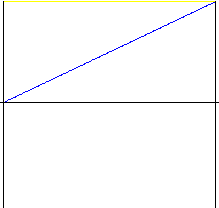
Liniowo
Ruch prosty o dużym skoku na początku i na końcu ruchu. Rzadko stosowany z wyjątkiem nieskomplikowanych urządzeń. Zaleca się stosowanie ruchu z modyfikowanego na początku i na końcu - parabolicznego z częścią liniową.
|
|
Skok |
|
|
Prędkość |
|
Skok |
f y (z) = z |
|
Prędkość |
f v (z) = 1 |
|
Przyspieszenie |
f a (z) = 0 |
|
Uwaga: Dla z = 0 i z = 1 poprawna wartość powinna być wartością nieskończoną, ale obliczenia nie będą współdziałać z wartościami nieskończonymi i stosowane są wartości zero.
|
|
|
Puls |
f j (z) = 0 |
|
Uwaga: Dla z = 0 i z = 1 poprawna wartość powinna być wartością nieskończoną, ale obliczenia nie będą pracować z wartościami nieskończonymi i stosowane są wartości zero.
|
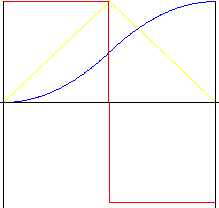
Paraboliczny (wielomian 2. nd stopnia)
Ruch z możliwie najmniejszym przyspieszeniem. Jednakże powstają wstrząsy z uwagi na nagłe zmiany przyspieszenia na początku, w trakcie oraz na końcu ruchu. Współczynnik odwrotności umożliwia "rozciągnięcie" środkowej części ruchu, co umożliwia zmianę współczynnika przyspieszenia i spowolnienia.
symetryczny (współczynnik odwrotności k r = 0,5)
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
dla z = 0 do 0,5: |
|||
|
Skok |
fy(z) = 2z 2 |
||
|
Prędkość |
fv(z) = 4z |
||
|
Przyspieszenie |
fa (z) = 4 |
||
|
Puls |
fa(z) = 0 |
||
|
dla z = 0,5 - 1: |
|||
|
Skok |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Prędkość |
fv(z) = 4 (1 - z) |
||
|
Przyspieszenie |
fa (z) = -4 |
||
|
Puls |
fj(z) = 0 |
||
|
Uwaga: Dla z = 0 i z = 1 poprawna wartość powinna być wartością nieskończoną, ale obliczenia nie będą pracować z wartościami nieskończonymi i stosowane są wartości zero.
|
|||
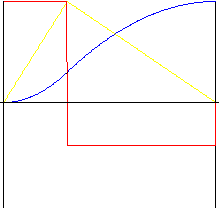
niesymetryczny
k r - współczynnik odwrotności (w zakresie 0,01 do 0,99)
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
dla z = 0 do k r : |
|||
|
Skok |
f y (z) = z 2 / k r |
||
|
Prędkość |
f v (z) = 2z / k r |
||
|
Przyspieszenie |
f a (z) = 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
dla z = k r do 1: |
|||
|
Skok |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Prędkość |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Przyspieszenie |
f a (z) = -2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
|
Uwaga: Dla z = 0 i z = 1 poprawna wartość powinna być wartością nieskończoną, ale obliczenia nie będą pracować z wartościami nieskończonymi i stosowane są wartości zero.
|
|||
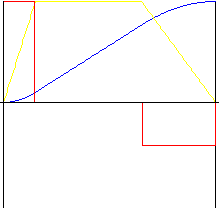
Parabola z częścią liniową
Zapewnia bardziej przystępne przyspieszenie i spowolnienie, niż ruch liniowy. Współczynnik odwrotności umożliwia "rozciągnięcie" środkowej części ruchu, co umożliwia zmianę współczynnika przyspieszenia i spowolnienia. Liniowa część ruchu umożliwia ustawienie względnej wielkości części liniowej ruchu.
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
k r - współczynnik odwrotności (w zakresie 0,01 do 0,99)
k l - współczynnik części liniowej (w zakresie 0 do 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
dla z = 0 do k r / k z : |
|||
|
Skok |
f y (z) = k h z 2 k z 2 / k r |
||
|
Prędkość |
f v (z) = 2 k h z k z 2 / k r |
||
|
Przyspieszenie |
f a (z) = 2 k h k z 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
dla z = k r / k z do r / k z + k l : |
|||
|
Skok |
f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l ) |
||
|
Prędkość |
f v (z) = 2 / (1 + k l ) |
||
|
Przyspieszenie |
f a (z) = 0 |
||
|
Puls |
f j (z) = 0 |
||
|
dla z = k r / k z + k l do 1: |
|||
|
Skok |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Prędkość |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Przyspieszenie |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
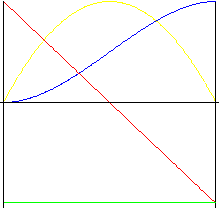
Wielomian 3. rd stopnia (parabola sześcienna)
W ruchu tym występują mniejsze wstrząsy niż w ruchu parabolicznym.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Skok |
f y (z) = (3 -2z) z 2 |
|
Prędkość |
f v (z) = (6 - 6z) z |
|
Przyspieszenie |
f a (z) = 6 - 12z |
|
Puls |
f j (z) = -12 |
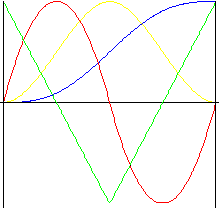
Wielomian 4. th stopnia
W ruchu tym występują mniejsze wstrząsy, niż w ruchu wg równania wielomianu 3. rd stopnia.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
dla z = 0 - 0,5 |
||
|
Skok |
f y (z) = (1 - z) 8z 3 |
|
|
Prędkość |
f v (z) = (24 - 32z) z 2 |
|
|
Przyspieszenie |
f a (z) = (48 - 96z) z |
|
|
Puls |
f j (z) = 48 - 192z |
|
|
dla z = 0,5 - 1 |
||
|
Skok |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Prędkość |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Przyspieszenie |
f a (z) = (48 - 96z) (1 - z) |
|
|
Puls |
f j (z) = 194z - 144 |
|
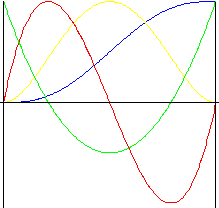
Wielomian 5. th stopnia
W ruchu tym występują mniejsze wstrząsy, niż w ruchu wg równania wielomianu 3. rd stopnia.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Skok |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Prędkość |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Przyspieszenie |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Puls |
f j (z) = (6z 2 - 6z + 1) 60 |
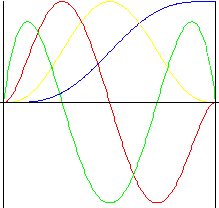
Wielomian 7. th stopnia
Ruch płynny we wszystkich równaniach, łącznie z pulsowaniem.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Skok |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Prędkość |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Przyspieszenie |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Puls |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
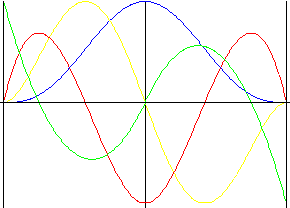
Niesymetryczny wielomian 5. th stopnia
Podobnie jak wielomian 5. stopnia, ale z wymuszoną rewersją skoku.
|
|
Skok |
|
|
Prędkość |
|
|
Przyspieszenie |
|
|
Puls |
|
Część 1 |
||
|
Skok |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Prędkość |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Przyspieszenie |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Puls |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Część 2 |
||
|
Skok |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Prędkość |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Przyspieszenie |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Puls |
f j (z) = (4z 2 - 3z) 40 |
|
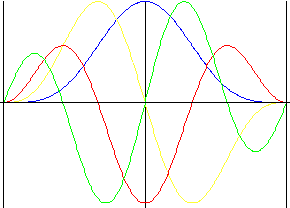
Podwójny harmoniczny
Ruch płynny we wszystkich równaniach, łącznie z pulsowaniem i z wymuszoną rewersją skoku.
|
Część 1 |
||
|
Skok |
f y (z) = cos(0,5π (1 - z)) 4 |
|
|
Prędkość |
f v (z) = π (0,5 sin(πz) - 0,25 sin(2πz)) |
|
|
Przyspieszenie |
f a (z) = 0,5 π 2 (cos(πz) - cos(2πz)) |
|
|
Puls |
f j (z) = π 3 (-0,5 sin(πz) + sin(2πz)) |
|
|
Część 2 |
||
|
Skok |
f y (z) = 1 - cos(0,5π z) 4 |
|
|
Prędkość |
f v (z) = π (0,5 sin(πz) + 0,25 sin(2πz)) |
|
|
Przyspieszenie |
f a (z) = 0,5 π 2 (cos(πz) + cos(2πz)) |
|
|
Puls |
f j (z) = -π 3 (0,5 sin(πz) + sin(2πz)) |
|
Porównanie maksymalnych wartości względnych
|
Ruch |
Prędkość |
Przyspieszenie |
Puls |
|
Cykloida (przedłużona sinusoida) |
2 |
6,28 |
39,5 |
|
Harmoniczny (sinusoidalny) |
1,57 |
4,93 |
15,5 |
|
Liniowy |
1 |
∞ |
∞ |
|
Paraboliczny (Wielomian 2. nd stopnia) |
2 |
4 |
∞ |
|
Wielomian 3. rd stopnia |
1,5 |
6 |
12 |
|
Wielomian 4. th stopnia |
2 |
6 |
48 |
|
Wielomian 5. th stopnia |
1,88 |
5,77 |
60 |
|
Wielomian 7. th stopnia |
2,19 |
7,51 |
52,5 |
|
Niesymetryczny wielomian 5. th stopnia |
1,73 |
6,67 |
40 |
|
Podwójny harmoniczny |
2,04 |
9,87 |
42,4 |
Inne zależności
Siła na rolce
|
F i = F + m a i + c y i [N, lb] |
Siła normalna
|
Fn i = F i / cos (γ i ) [N, lb] |
Moment
|
T i = F i r i tan (γ i ) [Nmm, funt cal] |
Nacisk jednostkowy (Hertz)
|
|
|
|
b = min (b v, b k ) |