W trakcie obliczeń płyt ortotropowych w każdym punkcie wyznaczana jest sztywność zastępcza na poziomie przekroju. Dla elementu powłoki płaskiej w 3D sztywność określona jest ona na podstawie macierzy:
- macierz sztywności tarczowej D
- macierz sztywności zginania K
- macierz sztywności ścinania H.
Biorąc pod uwagę założenie, że ortotropia definiowana jest jedynie dla elementów płaskich oraz że przekrój jest symetryczny, określenie macierzy sprzęgających stan giętny ze stanem membranowym nie jest konieczne.
Przekroje typów: żebrowanie jednokierunkowe dwustronne, strop skrzynkowy jednokierunkowy, strop skrzynkowy dwukierunkowy oraz gęstożebrowy ruszt są przekrojami symetrycznymi i dla nich powyższe podejście jest w pełni uzasadnione. Dla pozostałych typów powyższe założenie nie jest jednak dokładnie spełnione, stąd też proponowane podejście dla tych typów jest jedynie przybliżeniem.
Płaszczyznę odniesienia należy przyjmować raczej w poziomie środka ciężkości niż jako linię środkową (grubość płyty). Jest to bardziej poprawne podejście szczególnie wziąwszy pod uwagę drgania poprzeczne. Z punktu widzenia obliczania sztywności jest to jednak również przybliżenie, ale jest ono lepsze niż przyjęcie linii środka grubości.
Sztywność dla płyty określona jest na podstawie macierzy:
- macierz sztywności zginania K
- macierz sztywności ścinania H.
Sztywności (te odniesione do kierunków ortotropii) dane są przez macierze przyjmujące ogólną postać:
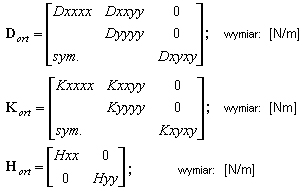
Kierunki ortotropii (a w zasadzie kierunek X) są określane przez użytkownika (definicja wektora kierunku) jak przy definicji układu lokalnego do prezentacji wyników czy zbrojenia V =[vx,vy,vz].
Reguły używane do określania, w jaki sposób zdefiniowany przez użytkownika wektor V generuje kierunek osi X układu ortotropii:
"Kierunek X jest kierunkiem stycznym do płaszczyzny elementu, który jest najbliższy zdefiniowanemu kierunkowi V".
Jeśli {e 1 ; e 2 ; e 3 } tworzą bazę lokalną w danym punkcie elementu (dla płyt w 2D,e i pokrywają się z kierunkami osi globalnych XG, YG) wówczas funkcje trygonometryczne sin α; cos α kąta a zawartego pomiędzy kierunkiem ortotropii X a osią lokalna x1 wyznacza się jako:
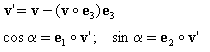
Po określeniu funkcji trygonometrycznych s =sin α; c =cos α kąta macierze sztywności są transformowane z układu osi ortotropii XY do kierunków lokalnych na elemencie z wykorzystaniem poniższych wzorów:
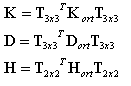
gdzie:
T3x3 jest macierzą transformowaną dla tensora 2—go rzędu w 2D (zapisanego jako macierz 3x3)
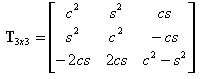
T2x2 jest macierzą reprezentującą transformacjaę wektora 2D
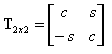
Zobacz także: