Równanie dotyczące przepływu ciepła wewnątrz konturu, jak pokazano na poniższym rysunku, może być wyświetlony w następujący sposób.
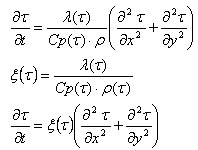
gdzie:
C p — ciepło właściwe (J/kg*K)
λ — przewodność cieplna (W/m*K)
ρ — obciążenie jednostkowe (kg/m3)
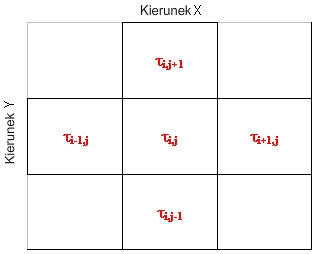
W innej notacji równanie przepływu można zapisać jako:
.
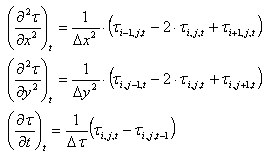Równania te dostarczają:
.
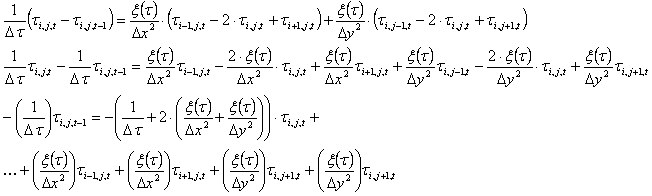Dlatego dla węzła K, system równań M [KxK] x τ [K] = B [K] będzie rozwiązany.
Przyjęta przybliżenia
Jeśli jest to wymagane, aby znać bieżącą temperaturę, w celu określenia współczynników, które nie są opisane za pomocą równań, przybliżenia z poprzednich kroków zapisu są stosowane (różnica progresywna).
Dla stałych kroków zapisu Δτ otrzymuje się następujące:
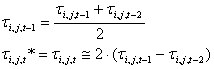
które umożliwia określenie:
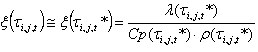
dla kroku i = 1 t i, j, 1 * = t i,j,o.
Warunki brzegowe
Do ogólnego sformułowania problemu, trzeci typ warunków brzegowych jest dodawane i jest on odpowiedzialny za:
- Konwekcję
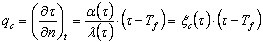
gdzie:
n — prostopadła do krawędzi
Tf — temperatura w środowisku zewnętrznym konturu, oznaczona ikoną odporności cieplnej.
Zakładając, że współczynnik konwekcji a jest niezależny od temperatury i przyjmuje przybliżenie omówione wcześniej, uzyskiwane jest:
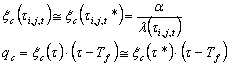. - Promieniowanie
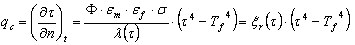
gdzie:
n — prostopadła do krawędzi
T f — temperatura w środowisku zewnętrznego konturu, oznaczona jako temperatura ognia
Φ — współczynnik konfiguracji
ε m — współczynnik wydzielania elementu
ε f — współczynnik wydzielania ciepła
σ — stała Boltzmana 5.65 * 10 8 (W/m 2 * K 4 ).
W wyniku przyjęcia przybliżeń omówionych wcześniej, uzyskiwane jest:
.
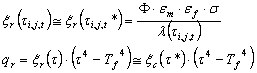Założenia przyjęte dla normy DTU P 92—701
- Rozprzestrzenianie się pożaru w czasie
Pożar opisany w formie niejawnej (tabelarycznie) na podstawie następującego wzoru:
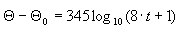(sekcja 4 DTU P 92-701, rysunek 11) Pożar opisany w formie niejawnej (tabelarycznie) na podstawie następującego wzoru:
gdzie t wyrażone jest w [min]
co pozwala na opisujanie temperatury ognia jako:
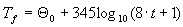
Dyskretne wartości są wybierane w taki sposób, aby żaden wzrost temperatury przekraczający 30% nie występował w żadnym okresie czasowym. Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis rozprzestrzeniania się ognia w czasie jest zawarty w pliku Fire_DTU.t
- Przewodność cieplna betonu
Zależność od przewodności cieplnej jest przedstawiana w formie tabelarycznej (sekcja 3.15 DTU P 92-701).
Opis zachowania przewodności cieplnej w zależności od temperatury jest określany w pliku Lambda_DTU.la.
- Obciążenie jednostkowe betonu
Jest on niezależny od temperatury i wynosi 2400 [kg/m3].
Opis zachowania obciążenia jednostkowego w zależności od temperatury jest określany w pliku Ro_DTU.cp.
- Ciepło właściwe betonu
Jest ono niezależne od temperatury i jest równe 921,096 [J/kg * K], czyli 0,22 [kcal/kg * OC] (sekcja 3.16 DTU P 92-701).
Opis zachowania ciepła właściwego w zależności od temperatury jest określany w pliku Cp_DTU.cp.
- Współczynnik redukcji dla nośności betonu
Współczynnik redukcji nośności betonu jest przedstawiany w formie tabelarycznej (sekcja 3.13 DTU P 92-701).
Opis zachowania redukcji nośności betonu w zależności od temperatury jest określone w pliku fic_DTU.cfc.
- Współczynnik redukcji dla nośności stali
Współczynnik redukcji nośności stali jest przedstawiany w formie tabelarycznej (sekcja 3.13 DTU P 92-701).
Opis zachowania redukcji nośności stali w zależności od temperatury jest określone w pliku fiy_DTU_1_2.cfy.
W przypadku, gdy typy stali 3 i 4 są używane, ustaw plik fiy_DTU_3_4.cfy, zamiast domyślnego.
- Parametry obliczeniowe
Współczynniki napromieniowania:
Φ*εm*εf = 0,85 analogicznie do współczynnika (sekcja 4 DTU P 92-701)
Powyższe współczynniki powinny być rozumiane jako:
Φ — współczynnik konfiguracji
εm — współczynnik wydzielania elementu
εf — współczynnik wydzielania ciepła
Współczynnik konwencji:
α = 6,9 [W/m2 * K] = 6,0 [kcal/m2*h*oC] (sekcja 4 DTU P 92-701)
Założenia przyjęte dla normy EN 1992—1—2
- Rozprzestrzenianie się ognia w czasie zgodnie z EN 1991—1—2
Pożar opisany w formie niejawnej (tabelarycznie) na podstawie następującego wzoru:
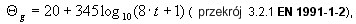
gdzie:
t wyrażone jest w [min]
przyjmując za punkt początkowy temperaturę 20 [ 0C]
co pozwala na opisujanie temperatury ognia jako:
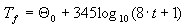. Dyskretne wartości są wybierane w taki sposób, aby żaden wzrost temperatury przekraczający 30% nie występował w żadnym okresie czasowym. Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis rozprzestrzeniania się ognia w czasie jest zawarty w pliku Fire_EC2_N.t.
W przypadku, gdy inne typy pożarów są użyte, zamiast domyślnego pliku, powinny zostać ustawionye następujące:
pożar zewnętrzny (sekcja 3.2.2 EN 1991-1-2): Fire_EC2_E.t
pożar węglowodorowy (sekcja 3.2.3 EN 1991-1-2): Fire_EC2_H.t
- Przewodność cieplna betonu
Zależność przewodności cieplnej jest przedstawiana w formie tabelarycznej (sekcja 3.4 EN 1992-1-2) —na podstawie niższe wartości przewodności cieplnej. Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis zachowania przewodności cieplnej w zależności od temperatury jest określany w pliku Lambda_DTU.la.
W przypadku, gdy górna wartość jest używana, zamiast domyślnego pliku, użytkownik powinien ustawić następujące opcje:
Lambda_EC2_U.la
- Obciążenie jednostkowe betonu
Zależność obciążenia jednostkowego jest przedstawiana w formie tabelarycznej (sekcja 3.3.2 (3) EN 1992-1-2). Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis zachowania obciążenia jednostkowego w zależności od temperatury jest określany w pliku Ro_DTU.cp.
- Ciepło właściwe betonu
Zależność ciepła właściwego jest przedstawiana w formie tabelarycznej (sekcja 3.3.2 (1) i 3.3.2 (2) EN 1992-1-2) na podstawie wartości dla wilgoci 1,5% . Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis zachowania ciężaru jednostkowego w zależności od temperatury jest określany w pliku Cp_EC2_m015.cp.
W przypadku, gdy inne wartości wilgotności betonu są używane, zamiast domyślnego pliku, ustaw następujące parametry:
wilgotność 0% : Cp_EC2_m000.cp
wilgotność 3% : Cp_EC2_m030.cp
- Współczynnik redukcji dla nośności betonu
Zależność współczynnika redukcji dla nośności betonu jest przedstawiana w formie tabelarycznej (sekcja 4.2.4.2 EN 1992-1-2) na podstawie wartości dla betonu z kruszywem silikatowym. Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis zachowania redukcji nośności betonu w zależności od temperatury jest określone w pliku fic_EC2_Si.cfc.
W przypadku, gdy używany jest beton z kruszywem wapiennym, zamiast domyślnego pliku, ustaw następujące parametry: fic_EC2_Ca.cfc.
- Współczynnik redukcji dla nośności stali
Zależność współczynnika redukcji dla nośności stali jest przedstawiana w formie tabelarycznej (sekcja 3.2.3 EN 1992-1-2) na podstawie wartości dla stali rodzaj N walcowanej na gorąco. Interpolacja liniowa jest wykonywane w określonym przedziale wartości.
Opis zachowania redukcji nośności stali w zależności od temperatury jest zawarta w pliku fiy_EC2_Nhr.cfy.
W przypadku, gdy inne typy są używane, zamiast domyślnego pliku, należy ustawić następujące parametry:
stal rodzaju N walcowana na zimno: fiy_EC2_Ncw.cfy.
stal rodzaju X: fiy_EC2_X.cfy.
- Parametry obliczeniowe
współczynniki napromieniowania:
Φ = 1,0 — współczynnik konfiguracji (sekcja 3.1 (6) EN 1991-1-2)
ε m = 0,8 — współczynnik wydzielania elementu (sekcja 3.1 (6) EN 1991-1-2)
ε f = 1,0 — współczynnik wydzielania ciepła (sekcja 3.1 (6) EN 1991-1-2)
współczynnik konwencji:
α ce = 25 [W/m2 * K] na stronie wystawionej na działanie ognia (sekcja 3.2.1 EN 1991-1-2)
α cu = 9,0 [kcal/m2*h*oC] na stronie nie wystawionej na działanie ognia (sekcja 3.1 (5) EN 1991-1-2)
Obliczenia nośności dla normy BAEL — słupy osiowo ściskany
Dane potrzebne do obliczeń:
f cj — wytrzymałość betonu automatycznie przeniesiona z modułu słupa żelbetowego programu Robot.
Φ b — współczynnik betonu w zależności od temperatury Φ b (τ), w tym przypadku τ to średnia temperatura wewnątrz przekroju
f e — wytrzymałość stali automatycznie przeniesiona z modułu słuba żelbetowego w prgramieRobot.
φ si — współczynnik dla stali w zależności od temperatury φ s(τ), w tym przypadku τ oznacza temperaturę w pręcie i—th
l — wysokość słupa
N — maksymalne obciążenie przyłożone do słupa
α — współczynnik automatycznie przeniesiony z modułu słupa żelbetowego
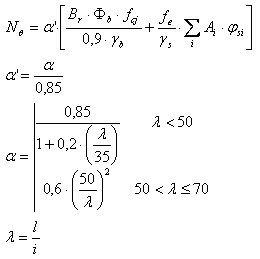
B r = A c — 0.0 *u c
Br — zmniejszone pole przekroju
A c — pole przekroju
u c — długość obwodu przekroju
γ b — współczynnik dla betonu 1.3
γ s — współczynnik dla stali 1.0
A i — obszar prętów zbrojeniowych i—th
Nośność słupa
N/NQ > 1.0