Opcja osiadania średniego jest dostępna w programie dla wszystkich norm za wyjątkiem norm francuskich (DTU 13.12 i Fascicule 62 Titre V). Włączenie analizy tego stanu oraz definicja wartości granicznej osiadań może zostać dokonana w oknie dialogowym Opcje geotechniczne.
Obliczenia osiadań średnich bazują na założeniach i wzorach liniowej teorii sprężystości. W szczególności obliczenia są oparte na naprężeniach wyliczanych ze wzoru Boussinesque’a i zasadzie superpozycji.
- Grunt pod fundamentem dzielony jest na pasma o grubości nie większej niż:
- połowa mniejszego wymiaru fundamentu
- 0,5 metra
- grubość warstwy gruntu
- Każde pasmo n jest analizowane na podstawie wartości obliczanych na głębokości będącej środkiem pasma Zn
- Dla głębokości Zn wyznaczane jest średnie naprężenie od obciążeń zewnętrznych, ciężaru fundamentu i gruntów nadległych s(z) pod fundamentem ze wzoru podanego poniżej
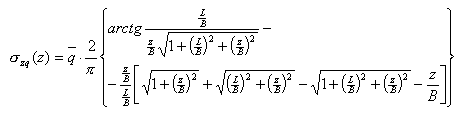
gdzie:
B — wymiar poprzeczny prostokąta (fundamentu)
L — wymiar podłużny prostokąta (fundamentu)
Inny sposób obliczeń jest wykorzystywany dla normy SNiP 2.02.01—83 (patrz poniższe opisy szczegółowe dla poszczególnych norm).
Powyższy wzór opisuje średnią wartość naprężeń pod obszarem prostokątnym. Jest on wyprowadzony ze wzoru Boussinesque’a, który opisuje rozkład naprężeń w półprzestrzeni sprężystej od obciążenia siłą skupioną.
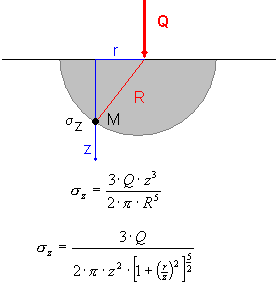
Wykorzystując zasadę superpozycji można obliczyć naprężenie w punkcie P(0,0,z) od dowolnego obszaru obciążonego obciążeniem równomiernym zgodnie z poniższą zasadą:
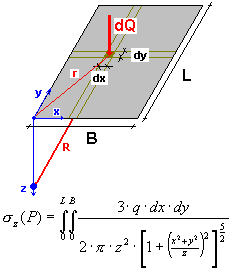
Rozwiązania powyższego równania dla punktów narożnych obszaru prostokątnego, pod środkiem prostokątnej powierzchni oraz wartości średniej pod obszarem prostokątnym są podane w literaturze. Aby uzyskać wartość naprężenia średniego pod obszarem prostokątnym, należy wykorzystać przedstawiony poniżej wzór, który po scałkowaniu przyjmuje postać użytą w algorytmie obliczeniowym.
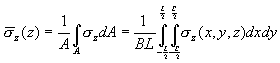
- Dla głębokości Zn wyznaczane jest naprężenie pierwotne pochodzące od gruntów zalegających powyżej analizowanego pasma.
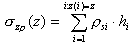
W przypadku występowania wód gruntowych, wypór hydrostatyczny wody oraz jej ciężar są uwzględniane w obliczeniach.
-
Naprężenia w gruncie dodatkowe uwzględniane w obliczeniach osiadań to różnica naprężeń wywołanych obciążeniem zewnętrznym i naprężeń pierwotnych
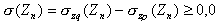
- Na podstawie charakterystyki gruntu oblicza się średnie osiadanie pasma n:
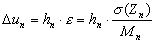
gdzie:
M 0n — to pierwotny (bez uwzględnienia efektów odprężenia) endometryczny (uzyskany w aparacie trójosiowego ściskania) moduł ściśliwości gruntu w n—tym paśmie. Zależność pomiędzy modułem Younga a endometrycznym modułem ściśliwości wyraża się wzorem
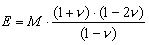 :
: Inny sposób obliczeń jest wykorzystywany dla normy SNiP 2.02.01—83 (patrz poniższe opisy szczegółowe dla poszczególnych norm).
W przypadku braku wartości współczynnika Poissona danego typu gruntu, bazy danych gruntów programu Robot dla poszczególnych krajów mogą zawierać wartości E = M, co odpowiada materiałowi idealnie ściśliwemu (n = 0.0); typowe wartości współczynnika Poissona wynoszą 0.2¸0.3 dla gruntów niespoistych (wartość 0.2 dotyczy gruntów gruboziarnistych jak żwiry, natomiast 0.3 gruntów drobnoziarnistych jak pyły) i 0.25¸0.37 dla gruntów spoistych (wartość 0.25 dotyczy gruntów silnie skonsolidowanych, natomiast 0.37 gruntów ilastych).
- Całkowite osiadanie gruntu jest sumą osiadań kolejnych warstw
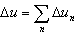
- Sumowanie warstw jest przeprowadzane aż do osiągnięcia odpowiednio małych naprężeń dodatkowych w porównaniu z naprężeniami pierwotnymi.
Dla poszczególnych wymagań narodowych stosowane są następujące ograniczenia i wymagania:
- ACI\ BS 8004:1986\ CSA Dla tych wymagań narodowych przeprowadzane jest sumowanie osiadań warstw aż do głębokości , na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 30%.
- DTU 13.12 \ Fascicule 62 Titre V
Obliczenia tego stanu granicznego nie są dostępne.
- ENV 1997-1:1994 (EC 7)
Obliczenia zaprezentowane w omówieniu ogólnym odpowiadają wymaganiom stawianym przez punkt 6.6.1 i Załącznik D. Dla tych wymagań narodowych przeprowadzane jest sumowanie osiadań warstw aż do głębokości , na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 20% [6.6.1] (2).
- EN 1997—1:2004 (EC 7)
Obliczenia zaprezentowane w omówieniu ogólnym odpowiadają wymaganiom stawianym przez punkt 6.6.1 i Załącznik D. Dla tych wymagań narodowych przeprowadzane jest sumowanie osiadań warstw aż do głębokości , na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 20% [6.6.2] (6).
- PN—81/B—03020
Obliczenia osiadań są przeprowadzane zgodnie z normowymi wymaganiami (punkt 3.5 i Załącznik 2). Wzory na naprężenia w gruncie podane w opisie ogólnym odpowiadają wzorom Z2—9 na naprężenia średnie pod obszarem prostokątnym oraz wzorowi 16 na naprężenia pierwotne (bez uwzględnienia efektów ciśnienia spływowego) i są wykorzystywane w obliczeniach.
W porównaniu z obliczeniami dla innych norm jest możliwe uwzględnienie efektów odciążenia gruntu poprzez wykop zgodnie z 3.5.1.2; efekty odciążania są obliczane jako ujemne naprężenia od obciążeń zewnętrznych równych ciężarowi usuniętego gruntu. Opcja ta jest dostępna w oknie dialogowym Opcje geotechniczne (opcja Czas realizacji budynku) i odpowiada ustaleniu normowej wartości l równej 0,0 lub 1,0 zgodnie z 3.5.3. Oznacza to, że całkowite osiadanie pasma gruntu obliczane jest ze wzoru:
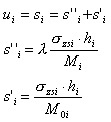
Drugi z powyższych wzorów jest identyczny ze wzorem na osiadanie pasma podanym w algorytmie ogólnym.
Dla polskiej normy przeprowadzane jest sumowanie osiadań warstw aż do głębokości, na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 30% naprężeń pierwotnych.
- SNiP 2.02.01—83
Obliczenia osiadań dla tej normy są przeprowadzane zgodnie z normowymi wymaganiami: punkt 2.39 i Załącznik 2.
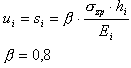
Naprężenia od obciążeń zewnętrznych są liczone na podstawie normowego wzoru Załącznika 2 (2):
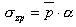
Współczynnik a jest określany na podstawie Załącznika 2 (Tabela 1). Pomiędzy wartościami tabelarycznymi wartości interpolowane są liniowo.
Przeprowadzane jest sumowanie osiadań warstw aż do głębokości, na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 20% naprężeń pierwotnych, a w przypadku gdy warstwa na tej głębokości ma moduł Younga o wartości E<5MPa lub warstwa bezpośrednio pod nią zalegająca ma taka wartość modułu, to obliczenia są prowadzone aż do głębokości, na której graniczna wartość naprężeń dodatkowych jest mniejsza niż 10% naprężeń (Załącznik 2 punkt 6).