Parametry drogi — określanie współczynników (mnożników obciążenia)

Działanie dla sił węzłowych

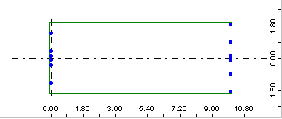
Jeżeli dla powyższego przykładu zdefiniowane zostaną wartości współczynników VP=1.3 i VL=0.9, obciążenie zostanie zamienione tak jak pokazano na poniższym rysunku.

• Dla sił N 1, 2 i 3

  Definicja pojazdu

  =>

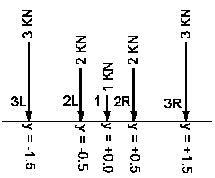
  Przyłożone siły

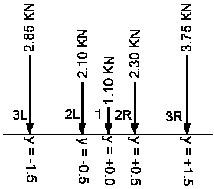
• dla sił N 4, 5 i 6

  Definicja pojazdu

  =>

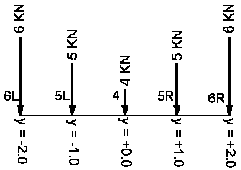
  Przyłożone siły

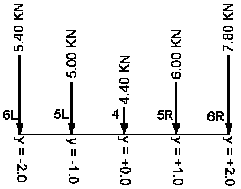
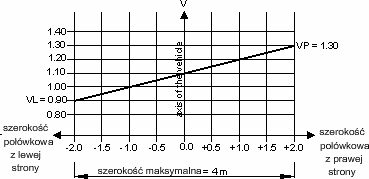
Aby otrzymać te wartości, należy poszukać wartości maksymalnej szerokości obciążenia, a następnie przemnożyć obciążenia odpowiadające maksymalnej szerokości przez znalezione wartości współczynników. Jeżeli obciążenie przyłożone jest w miejscu, którego szerokość jest mniejsza od maksymalnej, program Robot wyznaczy wartość współczynnika poprzez interpolację pomiędzy wartościami współczynników VL i VP w funkcji szerokości obciążenia.

Maksymalna szerokość = max ( S _i )

Uwzględnienie współczynników drogi VP,VL,HP,HL,LP,LL

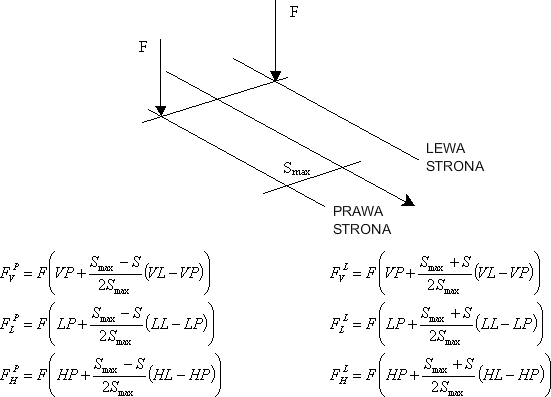
Działanie dla obciążeń liniowych

Dla obciążeń liniowych metoda postępowania jest taka sama jak dla sił węzłowych.

Działanie dla obciążeń powierzchniowych

W programie Robot istnieje możliwość zamiany obciążenia powierzchniowego jednorodnego na obciążenie powierzchniowe trapezowe (obciążenie powierzchniowe zdefiniowane przy pomocy trzech punktów).

Dla obciążeń powierzchniowych metoda postępowania jest taka sama jak dla obciążeń węzłowych i liniowych, z tym tylko, że maksymalna szerokość obciążenia wykorzystywana podczas interpolacji musi być obliczana biorąc pod uwagę wartości parametrów S i DY.

Maksymalna szerokość = max ( S _i + DY _i )

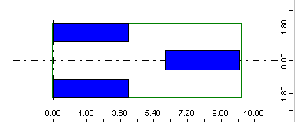
Zdefiniowane zostały wartości współczynników VP=1.3 i VL=0.9; dla tego przykładu maksymalna szerokość = max ( 3+1; 0+1) = 4 m

Funkcja rozkładu przedstawiona została na poniższym rysunku.

Program Robot zamienia obciążenie.

• Dla siły N 1

  Definicja pojazdu

  =>

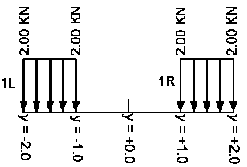
  Przyłożone siły

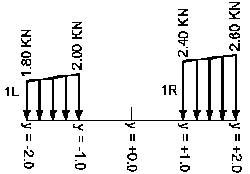
• dla siły N 2

  Definicja pojazdu

  =>

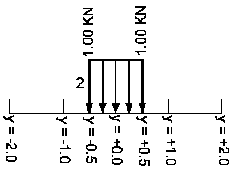
  Przyłożone siły

Uwaga: Rozkład sił dla współczynników LP i LL oraz HP i HL jest taki sam, jak dla współczynników VP i VL.

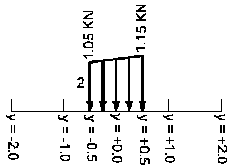
Rozkład obciążenia na elementy powierzchniowe

Obciążenia liniowe, powierzchniowe, skupione są zamieniane na swoje odpowiedniki obciążeń na elementach skończonych: liniowe na 2 punkty 2D (dla płyt), liniowe na 2 punkty 3D (dla powłok), obciążenie na konturze, siła w punkcie.