Uwagi wstępne:
Obciążenia, w zdecydowanej większości, powodowane są przez grawitację (masy). Dlatego dynamiczne obliczenia wymagają, aby wziąć te masy pod uwagę. Aby umożliwić użytkownikowi łatwą konwersję obciążeń statycznych (przeciążenie) w masy, w analizatorze plików tekstowych wykorzystano specjalne polecenie „MASess ACTive”.
To umożliwi użytkownikom zdefiniowane obciążenia jedynie raz dla celu statycznej analizy oraz potem do użycia ich w celu stworzenia dystrybucji mas w modelu obliczeniowym konstrukcji, aby wykonać jakąkolwiek analizę dynamiczną.
Polecenie wymaga dwóch elementów do pomyślnej konwersji. Pierwszy z nich to zestaw kierunków, w których masy są aktywne. Zwykle używane są wszystkie globalne kierunki (X, Y, Z), ponieważ tylko w specyficznych obliczeniach inercja działa nie działa na nie wszystkie. Drugi element to wielkość inercji. Jest on zdefiniowany przez numer przypadku statycznego obciążenia oraz przez kierunek obciążeń, które są brane pod uwagę w czasie konwersji. Ponadto może być podany dodatkowy współczynnik w celu pomnożenia wartości obciążenia.
Obciążenie jest automatycznie przekształcane na masę: siły skupione są przekształcane na masy skupione, momenty — na bezwładność w ruchu obrotowym, siły rozłożone — na masy ciągłe.
Składnia:
ANA [ DYN | MOD | TRAN | HAR | SEIsmic | SPEctral ],(dotyczy wszystkich typów analizy dynamicznej)
CASe (#<numer><nazwa>)
MASess ACTive [X/Y/Z]
[X|Y|Z ] (MINus|PLus) <case_list> COEfficient=<c>
Główne zasady:
Niech r = r(x) będzie funkcją rozkładu gęstości masy w danym elemencie, a N(x) macierzą funkcji interpolującej w danych węzłach (macierz funkcji kształtu). Jako podstawa przyszłej obróbki, zgodna macierz mas elementu będzie stworzona na podstawie następującej podstawowej formuły (1):
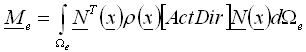 , (1)
, (1)
gdzie:
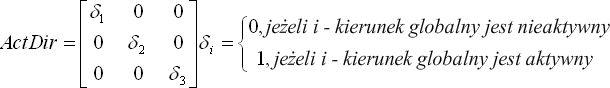
Flagi aktywności dla kierunku globalnego są ustalone za pomocą polecenia MASess ACTive [X/Y/Z], tzn. w przypadku użycia tego polecenia wszystkie kierunki są aktywne. Jest to konsekwencją sposobu pracy programu Robot z wartościami masy w przypadku, gdy niektóre składowe sił bezwładności mogą zostać pominięte w czasie analizy.
Macierz mas utworzona zostanie ze wszystkich obciążeń należących do wszystkich przypadków obciążeniowych określonych w <case_list>, działających na bieżący element/węzeł zgodnie z następującymi zasadami:
- Każdy rekord obciążeniowy z wybranego przypadku jest konwertowany na masę oddzielnie i niezależnie od innych obciążeń i mas.
- Wyłącznie proste przypadki obciążeniowe (bez kombinacji!) może pojawić się na liście (ale w jednym przypadku dynamicznym może być podana lista przypadków statycznych wymagajacych konwersji na masy).
- Macierz masy całkowitej stanowi sumę macierzy mas pochodzących ze wszystkich wyżej wymienionych składowych obciążenia i wstępnie określonej masy związanej z ciężarem własnym konstrukcji i/lub mas określonych elementów. Dlatego także część macierzy mas pochodząca od obciążeń zostanie poddana diagonalizacji i/lub — jeśli zostanie to określone w ustawieniach COH|CON, ROT — pominięta zostanie część powiązana z bezwładnością obrotową.
- Wartość funkcji gęstości w danym punkcie wynika z wartości rzutowania bieżącego wektora siły f na wektor n skierowanego w nowym, koniecznie określonym kierunku globalnym.
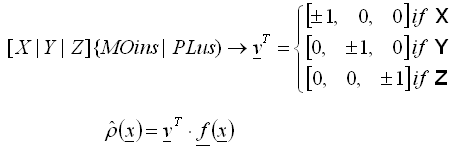 , (2)
, (2) - W każdym punkcie całkowania brane pod uwagę są tylko wartości dodatnie, dlatego
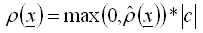 , (3) Uwaga: Powyższe zasady mają na celu ułatwienie wyboru obciążeń pochodzących od siły ciężkości. Ponieważ nie istnieje domyślny kierunek siły ciężkości, taki kierunek musi zostać określony przez użytkownika.
, (3) Uwaga: Powyższe zasady mają na celu ułatwienie wyboru obciążeń pochodzących od siły ciężkości. Ponieważ nie istnieje domyślny kierunek siły ciężkości, taki kierunek musi zostać określony przez użytkownika. - Wszystkie kierunki używane do definiowania konwersji obciążenia na masę muszą być zgodne z aktualnym, ogólnym typem konstrukcji, stąd typ PLAte jest zgodny tylko z kierunkiem Z, a w przypadku innych typów konstrukcji powierzchniowych dostępne są tylko kierunki X oraz Y. Niezgodne specyfikacje dla kierunku zostaną zignorowane lub wyświetlona zostanie informacja o błędzie. Dla przestrzennych typów konstrukcji akceptowane są wszystkie kierunki globalne.
Przykład:
Wyobraźmy sobie belkę, obciążoną centralnie przez obciążenie grawitacyjne Fy= - 120 kN. Załóżmy, że przypadek statyczny poniżej ma numer 3. Aby wyliczyć postać wolnych drgań dla tej konstrukcji w przypadku numer 10, biorąc pod uwagę tę masę (Fx=Fy= 12 232 kg), można użyć następującego polecenia:
ANA MOD=3 MAS=CON
CAS #10 modal
MASses ACTive X Y
Y MINus 3

Szczegółowe informacje na temat konwertowania różnych typów obciążenia
Obciążenia działające na elementy belek
- obciążenie równomierne elementu
[Px=<px.>/Py=<py>/Pz=<pz>] (LOCal/GLObal) (PROjected) ([R=<r>])([R=<r>])
Wektor gęstości obciążenia jest przekształcany w globalne kierunki zgodnie z podanymi ustawieniami:
(LOCal/GLObal) (PROjected) ([R=<r>]), przy uwzględnieniu flagi (PROjected) tak jak w przypadku obciążenia, wówczas równomierny rozkład masy jest ustalony zgodnie z (2) (3)
- obciążenie stałe
Obciążenie stałe jest konwertowane na masę odpowiednio do obciążeń rozłożonych.
Uwaga: Ta operacja powinna być używana z rozwagą, ponieważ masa powstała z ciężaru własnego konstrukcji jest automatycznie brana pod uwagę w dynamicznych obliczeniach (jeśli tylko gęstość materiału jest większa niż 0). - obciążenie zmienne elementu
(X=<x1>)[ P=<p1>] ((JUSque)(X =<x2>)[P=<p2>] ) (R=<r>) (LOCal/GLObal) (RELative) (PROjected)
obciążenie jest przekształcane w globalne kierunki zgodnie z podanymi ustawieniami:
(LOCal/GLObal) (PROjected) ([R=<r>])
następnie dystrybucja rozłożonych mas jest ustawiana odpowiednio na (2)(3)
Uwaga: Zasada (3) narzuca następującą obróbkę zmiennej obciążenia, dla każdego rekordu (komponentu) obciążenia osobno (nie dla całkowitego obciążenia będącego sumą wszystkich obciążeń działających na dany element), jak pokazano na Rys 1.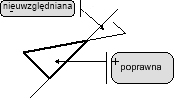 Rys.1
Rys.1 - siła skupiona elementu
[X=<x>] [F=<f>](R=<r>) (Local)(RELative)
Masa całkowita m skupiona w punkcie x 0 jest szacowana na podstawie globalnego przedstawienia wektora siły f w następujący sposób:
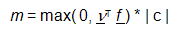 , (4)
, (4) W następnej kolejności szacowana jest rozłożona macierz mas, tak jak gdyby rozkład masy został przedstawiony za pomocą delty Diraca, co spowoduje:
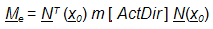 , (5)
, (5) - moment skupiony elementu
[X=<x>] [F=<fc>] (R=<r>) (LOCal)(RELative)
Ponieważ specyfikacja kierunku mas nie dotyczy kierunków bezwładności w ruchu obrotowym, dlatego osobna zasada powinna być przyjęta aby wykonać konwersję pomiędzy momentem skupionego elementu oraz bezwładnością w ruchu obrotowym określonego ciała dołączonego do elementu.
Transformacja stylu wektora <fc> wykonywana jest zgodnie z ustawieniami (R=<r>) (LOCal), aby uzyskać wektor I odnoszący się do lokalnego układu współrzędnych elementu. Aby uniknąć konieczności przekształcania wektora niekonsystentnego (w sytuacji gdy wymagany jest tensorowy), powinno zostać podane obciążenie LOCal, a nie R=<r>, w przeciwnym przypadku wyświetlone zostanie ostrzeżenie.
Przyjmuje się, że współrzędne lokalne elementu pokrywają się z główną osią bezwładności ciała, dlatego
 przedstawiają główne momenty bezwładności we współrzędnych lokalnych elementu. Z tego wynikają następujące ograniczenia modelowania:
przedstawiają główne momenty bezwładności we współrzędnych lokalnych elementu. Z tego wynikają następujące ograniczenia modelowania: 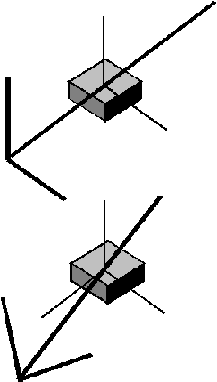
Rys. 2
Poprawna sytuacja
Niepoprawna sytuacja, modelowanie niemożliwe.
- moment rozłożony elementu
[M=<m>] (LOCal)
W tej definicji <m> jest wektorem, który po transformacji wektorowej na lokalny układ współrzędnych elementu przedstawia gęstości bezwładności w ruchu obrotowym, odnoszące się do osi lokalnej elementu i jego długości.
Wszystkie pojęcia dotyczące momentu skupionego elementu, (zobacz Rys. 2), pozostają.
Obciążenia działające na elementy powierzchni
- obciążenie równomierne elementu
[Px=<px.>/Py=<py>/Pz=<pz>]
Wektor gęstości obciążenia jest obliczany, następnie przekształcany w gęstość masy odpowiednio do (2)(3)
- obciążenie stałe
Obciążenie stałe jest konwertowane do odpowiedniego obciążenia jednorodnego oraz przyszłej obróbki jak powyżej
Uwaga: Ta operacja powinna być używana z rozwagą, ponieważ masa powstała z obciążenia stałego konstrukcji jest automatycznie brana pod uwagę w obliczeniach (jeśli tylko gęstość materiału jest większa niż 0) - obciążenie zmienne elementu
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>))
W każdym punkcie scalenia jest obliczana gęstość obciążenia, następnie przekształcana jest w gęstość masy odpowiednio do (2)(3), zobacz Rys. (1). Wykorzystywane są zasady ulepszonego scalenia
NGAUS = 3x3 dla Q8,
= 7 dla T6,
= 2x2 dla Q4
= 3 dla T3
- obciążenie zmienne wewnątrz konturu
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>)) PROjected DIRection <v> _CONtour <l_node>
W każdym punkcie scalenia jest obliczana gęstość obciążenia, następnie przekształcana jest w gęstość masy odpowiednio do (2)(3), zobacz Rys. (1). W przypadku, gdy nie cały obszar elementu należy do konturu, wykonywane jest w pełni automatyczne scalenie w obszarze do 100x100 punktów siatki, aby uzyskać wymaganą precyzję scalenia. Dlatego użycie tej opcji może czasami spowolnić proces obliczenia macierzy masy.
- obciążenie zmienne wzdłuż linii
LIN
<n1>[P=<p1>] Jusque <n2> (P=<p2>) ( [LOCal (GAMma=<gamma>)] )
Tylko siła translacyjna może być skonwertowana do masy elementu rozłożonego wzdłuż linii.
Zasada scalenia typu 3-punktowego prawa Gaussa jest stosowana do używana w każdym segmencie linii krzyżującej się z elementem. W każdym scaleniu, wektor gęstości obciążenia jest przekształcany w globalne koordynaty systemu, następnie przetwarzany zgodnie z (2)(3) do wyliczenia dystrybucji masy wzdłuż linii.
- obciążenie skupione w punkcie pomocniczym
NODe (węzeł pomocniczy)
F=<f> ( [R=<r>] )
Tylko siła translacyjna może być skonwertowana do masy elementu (dla momentu elementów belki — konwersja bezwładności w ruchu obrotowym jest dozwolona, tutaj jest zabroniona). Wektor siły <f>, jeśli to konieczne, jest przenoszony do globalnego układu współrzędnych, a następnie objęty procedurą zgodnie z (2),(3) w celu oszacowania wartości masy przyłożonej do danego punktu w elemencie. Następnie, zgodnie z (5), szacowana jest macierz mas. Element, do którego będzie dołączona masa, jest wyszukiwany automatycznie.
Obciążenia węzłowe
- siła skupiona
NODe
F=<f> ( [R=<r>] )
Wektor siły <f> traktowany zgodnie z (2)(3), aby ocenić wartość masy węzłowej
- moment skupiony
NODe
F=<c> ( [R=<r>] )
Ponieważ opis kierunku masy nie dotyczy kierunków bezwładności w ruchu obrotowym pomiędzy skupionym węzłowym momentem a bezwładnością w ruchu obrotowym dla danego ciała dołączonego do węzła.
Transformacja stylu wektora <fc> wykonywana jest zgodnie z ustawieniem (R=<r>), aby uzyskać wektor
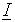 , odnoszący się do globalnego układu współrzędnych. Aby uniknąć konieczności przekształcania wektora niekonsystentnego (w sytuacji gdy wymagany jest tensorowy), nie należy podawać obciążenia LOCal ani R=<r>, w przeciwnym przypadku wyświetlone zostanie ostrzeżenie.
, odnoszący się do globalnego układu współrzędnych. Aby uniknąć konieczności przekształcania wektora niekonsystentnego (w sytuacji gdy wymagany jest tensorowy), nie należy podawać obciążenia LOCal ani R=<r>, w przeciwnym przypadku wyświetlone zostanie ostrzeżenie. Przyjmuje się, że współrzędne globalne elementu pokrywają się z główną osią bezwładności ciała, dlatego
 przedstawiają główne momenty bezwładności we współrzędnych globalnych elementu. Uwaga: Ta zasada jest inna niż te użycie w przypadku masy rozłożonej dołączonej do elementu belki.
przedstawiają główne momenty bezwładności we współrzędnych globalnych elementu. Uwaga: Ta zasada jest inna niż te użycie w przypadku masy rozłożonej dołączonej do elementu belki.