Podstawy teoretyczne metod używanych podczas analizy dynamicznej konstrukcji

Wprowadzenie

Ten dokument zawiera opis metod analizy dynamicznej stosowanych w programie Robot. W dodatkach są przedstawione szczegółowe założenia teoretyczne oraz przykłady. W sekcji tej nie ma natomiast instrukcji praktycznych oraz odniesień do interfejsu programu Robot. Są w niej wyłożone zasadnicze koncepcje, na których opiera się działanie tego programu.

Podstawą większości metod dynamicznych używanych w programie Robot są wyniki analizy modalnej. Przede wszystkim należy wiedzieć, że metody analizy modalnej zależą od wybranego typu solwera. W przypadku solwera skyline są dostępne następujące metody: blokowa iteracja podprzestrzenna (BLSI, block subspace iteration), iteracja podprzestrzenna (SI, subspace iteration), algorytm Lanczosa i podstawowa metoda redukcji. W przypadku bezpośredniego solwera rzadkiego dostępna jest metoda BLSI (blokowa iteracja podprzestrzenna), algorytm Lanczosa i podstawowa metoda redukcji. Jeśli chodzi o solwer iteracyjny, dostępne są następujące metody: zmodyfikowany algorytm Lanczosa (tryb pseudo — patrz 3.5 i dodatki 3A, 3B), metoda gradientów Ritza (PCG_Ritz) i metoda gradientów sprzężonych z przyśpieszaniem (PCG).

Bezpośredni solwer sparse (SPDS) to specyficzna odmiana eliminacji Gaussa. Jest to najbardziej zalecany solwer do analizy problemów o średniej i dużej skali (od 10 do 200 tysięcy równań) oraz dobry zamiennik solwera iteracyjnego.

3.1. Metoda analizy modalnej

Analiza modalna składa się z dwóch podstawowych działań. Analiza wartości własnych

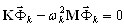k = 1,2,…,N (3.1)

wynikająca z definicji wartości własnych wk i wektorów własnych 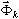. Jest to pierwsze działanie dobrze znane inżynierom. Drugie działanie polega na generowaniu wektorów podstawowych

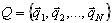(3.2)

i poszukiwaniu przybliżeń Ritza , (k=1,2,….,N). Jest ono oparte na metodzie wektorów Ritza zależnych od obciążenia, zaproponowanej przez E.L. Wilsona [1, 3] i wykorzystanej w programie SAP2000. To działanie jest stosowane to analizy sejsmicznej i świetnie sprawdza się w sytuacjach, gdy bardzo trudno jest uzyskać wystarczający procent masy (patrz sekcja 3.5).

W połączeniu z solwerami bezpośrednimi (skyline i SPDS) stosowane są metody BLSI i SI, algorytm selektywnej ortogonalizacji Lanczosa i podstawowa metoda redukcji (patrz Dodatek 3A). Metoda SI jest zazwyczaj bardzo powolna. W związku z tym w przypadku analizowania problemów średniej, a zwłaszcza dużej skali, które wymagają dużej liczby par właściwych, zalecane jest zastosowanie metody BLSI lub algorytmu Lanczosa. Podstawowa metoda redukcji może okazać się bardzo skuteczna w rękach doświadczonego inżyniera; wymaga ona jednak dodatkowych informacji o podstawowych węzłach i właściwych kierunków podstawowych.

Metoda gradientów sprzężonych z przyspieszaniem (PCG)

Ta metoda jest używana w przypadku wyboru solwera iteracyjnego. Działanie to może być bardzo skuteczne, jeśli zostanie wyodrębniona niewielka liczba postaci drgań własnych (najwyżej 5). Należy jednak z niego korzystać raczej do analizy wiatru niż do analizy sejsmicznej. Przy użyciu metody PCG można wyznaczyć najniższą postać drgań własnych w przypadku napotkania problemu o dużej skali.

Drugie działanie (realizowane poprzez analizę trybu pseudo) jest zaprezentowane w sekcji 3.5.

Blokowa iteracja podprzestrzenna (BLSI)

Ta metoda [1,3] jest bardziej ogólna niż algorytm Lanczosa, ponieważ umożliwia implementację wszystkich typów macierzy mas (patrz sekcja 3.2) i nadaje się do analizy oddzielnych konstrukcji. Iteracje prowadzone w bloku o stałym rozmiarze, z natychmiastowym wykluczeniem zbieżnych wektorów i dodaniem nowych wektorów startowych, sprawiają zazwyczaj, że przebieg obliczeń jest szybszy niż w przypadku tradycyjnej metody iteracji podprzestrzennej [1-3]. Podobnie jak algorytm Lanczosa metodę BLSI można zastosować do wyodrębnienia dużej liczby par własnych (do 100–200).

Iteracja podprzestrzenna (SI)

Ta metoda może służyć do analizy wszystkich typów macierzy mas [4] i analizy oddzielnych konstrukcji, jednak w przypadku dużej liczby wymaganych postaci (około N > 10), jest ona bardzo czasochłonna, zwłaszcza jeśli wystąpi problem o dużej skali.

Algorytm Lanczosa [12,16,17] jest bardzo skuteczną metodą, która umożliwia uzyskanie dużej liczby par własnych (N ~ 20–500 i więcej). Chociaż jest preferowaną metodą w przypadku problemów o dużej skali, to podlega następującym ograniczeniom:

Nie można analizować oddzielnych konstrukcji.
Macierze mas powinny być skupione z rotacjami lub rozłożone.
Nie można zignorować gęstości materiału (chociaż wystarczy wyznaczyć niewielką fikcyjną gęstość, aby pominąć to ograniczenie).

Podstawowa metoda redukcji

Ta metoda [5] jest nazywana udoskonaloną metodą Rayleigha-Ritza [4] lub metodą Bubnowa-Galerkina w układach dyskretnych. Algorytm ten umożliwia uzyskanie wartości przybliżonych pierwszych kilku par własnych, jeśli niektóre informacje o nich są znane. Metoda wymaga zdefiniowania stopni swobody typu „master” (MDOF — „master degree of freedom”) w celu uzyskania układu zredukowanego. Dlatego proces tworzenia zmniejszonego modelu mogą być kontrolowany. Jest to potężne narzędzie dla tych, którzy posiadają doświadczenie w dynamicznej analizie konstrukcji i pracują z tego samego typu konstrukcjami, których zachowanie jest znane. Ta metoda umożliwia wykluczenie niepożądanych stopni swobody (DOF) ze zredukowanego modelu i zredukowanie początkowo złożonego problemu z dużą liczbą stopni swobody do formy zredukowanej. Jest to osiągane przy znacząco zredukowanej liczbie stopni swobody. Doświadczenie dotyczące analizy dynamicznej konstrukcji pokazuje, że niektóre problemy mogą zostać wykryte przez użytkownika, gdy automatyczna metoda redukcji (BLSI, SI i Lanczos są brane pod uwagę) prowadzi do bardzo złożonych obliczeń. Na przykład, tryby lokalnego drgania pojedynczych prętów mogą prowadzić do poważnych problemów, ponieważ proces obliczania szuka par własnych automatycznie bez żadnego wyboru. Tak powinno być dla większości przypadków w rzeczywistych konstrukcjach. W przeciwnym wypadku lokalne drgania zostaną ograniczone przez niektóre więzy, które nie są brane pod uwagę w modelu FEM, lub ich udział nie będzie konieczny w całkowitym ruchu systemu. Zazwyczaj procent masy jest bardzo mały w takim lokalnym drganiu. Użycie dokładnych metod, w tym przypadku będzie prowadzić do wyżej wspomnianych problemów. Natomiast zastosowanie przybliżonej metody redukcji podstawowej może znacznie uprościć proces obliczeniowy.

Metoda gradientów sprzężonych z przyspieszaniem (PCG)

Tę metodę [9-13] można stosować w połączeniu z solwerami iteracyjnymi. Jest ona zalecana w celu wyodrębnienia niewielkiej liczby par własnych w przypadku napotkania problemu o dużej skali. Jeśli podczas przeprowadzania analizy sejsmicznej lub spektralnej trzeba wyznaczyć dużą liczbę postaci, gdy jest wybrany solwer iteracyjny, wskazane jest zastosowanie trybu pseudo (patrz 3.5) ze zmodyfikowanym algorytmem Lanczosa lub PCG_Ritz.

Gradient Ritza (PCG_Ritz)

Tę metodę [8] można stosować w połączeniu z solwerami iteracyjnymi w trybie pseudo. Umożliwia ona uzyskanie przybliżonego rozwiązania w zakresie wektorów Ritza. Przyspiesza to znacznie wykonywanie analizy sejsmicznej i spektralnej średniej skali (od 10 do 100 tysięcy równań).

Zmodyfikowany algorytm Lanczosa

Ta metoda jest rozszerzeniem algorytmu Lanczosa i jest stosowana w połączeniu z solwerem iteracyjnym. Podobnie jak algorytm Lanczosa działa w trybie pseudo. Jednakże, w odróżnieniu od algorytmu Lanczosa używanego w połączeniu z solwerami bezpośrednimi, nie wymaga faktoryzacji macierzy sztywności. Zamiast tego stosowane są zasady metody gradientów z przyspieszeniem. Działanie to jest najskuteczniejsze, chociaż często nie najszybsze, ze wszystkich dynamicznych metod solwerów iteracyjnych.

Szczegółowy opis wszystkich metod dynamicznych jest przedstawiony w dodatku 3A.

3.2. Typy macierzy mas

Do konstrukcji można zastosować macierz mas analizy dynamicznej skupioną bez rotacji, skupioną z rotacjami i rozłożoną.

Macierz mas skupiona z rotacjami i macierz mas skupiona bez rotacji są diagonalnymi macierzami mas. Te typy macierzy mas wymagają najmniejszego nakładu pracy obliczeniowej.

Rozłożona macierz mas występuje wtedy, gdy jest rozpatrywany układ z parametrami rozproszonymi. Uważa się powszechnie, że rozłożona macierz mas bardziej precyzyjnie wyraża właściwości inercyjne konstrukcji niż skupiona. Mimo to przybliżenie uzyskane dzięki zastosowaniu skupionej macierzy mas jest na ogół wystarczająca ze względu na to, że parametry inercyjne można przedstawiać mniej precyzyjnie niż sztywność. W praktyce energia kinetyczna jest opisana jako przemieszczenia konstrukcji, a energia potencjalna jest wyrażana poprzez pochodną przestrzenną przemieszczeń. Dobrze wiadomo, że błąd przybliżenia znacznie wzrasta za każdym różniczkowaniem [4]. W związku z tym w przypadku obiektów ciągłych (bryła, powłoki, płytki) przybliżenie parametrów masy może być mniej precyzyjne niż sztywności przy tej samej siatce.

Jako funkcje kształtu w przypadku prętów zazwyczaj są stosowane wielomiany Hermite'a. Jest to dokładne rozwiązanie większości problemów statycznych i problemów dynamicznych, jeśli jest rozpatrywana skupiona macierz mas. Dokładne rozwiązania problemów dynamicznych pręta z rozkładem mas należą jednak do klasy funkcji Kryłowa (specyficzne połączenie funkcji hiperbolicznych i trygonometrycznych). Pozwala to przedstawić w przybliżeniu parametry sztywności podczas stosowania wielomianów Hermita w połączeniu z rozłożoną macierzą mas. Nie służą do implementacji różnego typu funkcji kształtu w przypadku problemów statycznych i dynamicznych. W większości przypadków komplikowanie modelu dynamicznego przez użycie parametrów rozkładu mas nie daje zatem zbyt wiele pożytku, ponieważ powoduje tylko zastąpienie dokładnego rozwiązania modelu przybliżonego (masy skupione) przybliżonym rozwiązaniem rozłożonych mas.

Ponadto masy pręta elementów konstrukcyjnych (dźwigary, słupy, itp.) są zazwyczaj pomijalne w porównaniu z masami ścian i dachu (obciążenie statyczne), które są brane pod uwagę przez przekształcenie obciążenia statycznego na masy. Takie masy niekonstrukcyjne zwykle zmniejszają efekty mas elementów rozproszonych.

W praktyce skupiona macierz mas na ogół zapewnia wystarczająco precyzyjne przybliżenie nieinercyjnych właściwości konstrukcji. Należy pamiętać, że rozłożona macierz mas wymaga znacznego nakładu pracy obliczeniowej podczas analizowania problemu o dużej skali. Wybór rozłożonej macierzy mas do analizy musi zatem być odpowiednio uzasadniony.

Przyjmuje się, że macierz mas musi być rozłożona, jeśli w modelu obliczeniowym są używane sztywne połączenia.

Jeśli jest stosowany bezpośredni solwer sparse lub solwer iteracyjny, iloczyn macierzy i wektora uzyskuje się przez użycie techniki „element po elemencie” (EBE). Rozłożonej macierzy mas nie można złożyć w żadnej sytuacji, ale wszystkie operacje są wykonywane tylko na poziomie elementów. W przypadku solwera skyline rozłożona macierz mas jest składana i przechowywana w taki sam sposób jak macierz sztywności. Jeśli problem jest mały (nie więcej niż 3000 równań), technika skyline jest szybsza, chociaż czas, jaki pochłania, rośnie proporcjonalnie do skali problemu.

Możliwe jest użycie dodanych mas i przekształcenie obciążeń statycznych na masy.

W połączeniu z algorytmem Lanczosa, metodą PCG_Ritz i zmodyfikowanym algorytmem Lanczosa (solwer iteracyjny) można stosować tylko skupioną macierz mas z rotacją i rozłożoną macierz mas.

3.3. Górne limity

Możliwe jest obliczenie wszystkich wartości własnych i postaci drgań własnych, które nie przekraczają wartości zdefiniowanej przez użytkownika. Wartość ta jest traktowana jako „górny limit”. Po włączeniu program Robot wyszukuje ω₁, ω₂, …, ω_n ≤ ω^*, gdzie ω^* jest górnym limitem. Algorytm działa w dwóch etapach. W trakcie pierwszego etapu jest wykonywane wyszukiwanie sekwencji Sturm w celu określenia liczby wartości własnych n, która jest mniejsza od górnego limitu. W trakcie drugiego etapu algorytm generuje n par własnych, z których każda jest mniejsza od górnego limitu.

Ze względu na konieczność uzyskania dużej liczby par własnych zalecanymi metodami w typach analizy, w których jest stosowany górny limit, jest algorytm Lanczosa i BLSI.

Włączenie górnego limitu powoduje, że jest ignorowane kryterium procentu mas udziału (patrz sekcja 3.4).

Problemy mogą np. wystąpić w przypadku stosowania francuskiej normy odporności sejsmicznej PS—92, która nakazuje branie pod uwagę wszystkich częstotliwości mniejszych niż 33 Hz.

3.4 Procent mas udziału

Procent mas poszczególnych postaci (k=1,2,…,N) jest definiowany jako

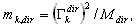
gdzie 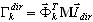, 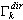jest współczynnikiem udziału mas dla postaci drgań własnych k, I_dir jest wektorem translacji jednostkowej w kierunku (dir = X,Y,Z), 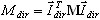jest całkowitą masą w kierunku dir, 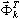jest k—tą postacią drgań własnych, .

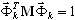Procent mas w kierunku dir równa się M%dir 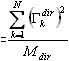. Definiuje on rozkład wszystkich postaci występujących w ruchu konstrukcji w rozważanym kierunku.

Jeśli jest wybrana analiza modalna i procent mas danej maksymalnej liczby węzłów jest mniejszy niż jest to wymagane, zostanie wyświetlone ostrzeżenie o nieodpowiednim procencie mas i obliczenia będą kontynuowane bez żadnych poprawek.

Aby wymagany procent mas był wyszukiwany automatycznie, konieczne jest ustawienie trybu sejsmicznego lub pseudo. Szczegóły zawiera sekcja 3.5.

3.5. Tryby analizy

W tej sekcji są przedstawione dynamiczne tryby analizy — analiza modalna, sejsmiczna i pseudo.

Niektóre normy odporności sejsmicznej (UBC—97, francuska PS—92) wymagają, aby suma mas w każdym kierunku (lub tylko w kierunkach poziomych) była nie mniejsza niż 90%. Jeśli wymagana suma mas zostanie uzyskana wskutek niewielkich wkładów dużej liczby najniższych postaci, mogą powstać problemy. Zazwyczaj jest to spowodowane lokalnym charakterem najniższych postaci. Tryb sejsmiczny i pseudo służą do naprawy sytuacji w razie wystąpienia takich trudnych problemów. Skuteczność tych działań jest zilustrowana w dodatku 3C. W tych dwóch trybach jest dostępny algorytm Lanczosa dla solwerów bezpośrednich. W trybie pseudo jest dostępny zmodyfikowany algorytm Lanczosa i PCG_Ritz pod warunkiem, że jest wybrany solwer iteracyjny.

Modalna

Tryb ten jest o tyle dobrze znany, że był zaimplementowany w poprzednich wersjach programu Robot.

W przypadku solwerów bezpośrednich są dostępne metody BLSI i SI oraz algorytm Lanczosa i podstawowa metoda redukcji, natomiast w przypadku solwera iteracyjnego jest dostępna metoda PCG.

Kryteria zbieżności dla solwerów bezpośrednich są następujące: Iteracje zostaną zatrzymane, gdy 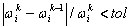, gdzie i = 1, 2,..., N; K jest numerem iteracji, N liczbą postaci (zdefiniowaną przez użytkownika). The basis reduction method does not produce the convergence check, since it is not the iterative approach, although it is a kind of Ritz method. Aby poprawić precyzję wyniku, należy zwiększyć liczbę głównych stopni swobody.

Kryteria zbieżności metody PCG (solwer iteracyjny) są następujące:

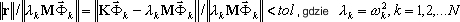
Szczegóły są opisane w załączniku 3A.

Górne limity to dolna wartość graniczna okresu, częstotliwości i pulsacji. Jeśli ten parametr jest różny od 0, zostaną obliczone wszystkie kolejne pary własne od 0 do górnego limitu.

%masy to procent masy (suma mas wszystkich obliczonych postaci w poszczególnych kierunkach).

Weryfikacja Sturm to wyszukiwanie pominiętych par własnych między 0 a parametrem przesunięcia , które polega na zliczaniu ujemnych elementów na przekątnej rozłożonej przesuniętej macierzy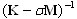

Jest to bardzo kosztowna procedura w przypadku problemów o dużej skali. Należy zwrócić uwagę, że w przypadku analizy sejsmicznej i spektralnej uzyskanie ciągłego spektrum wartości własnych jest zbędne. Ważne jest, aby modalny procent mas w każdym kierunku był wystarczający. Jeśli ten warunek jest spełniony, podstawa będzie kompletna. Implementowanie metody BLSI umożliwia dokonanie częściowej weryfikacji ciągłości spektrum wartości własnych bez przeprowadzania weryfikacji Sturm. Więcej informacji zawiera opis metody BLSI.

Liczba postaci	Górne limity	%masy	Zachowanie programu
N	0 (nieaktywne)	0 (nieaktywne)	Pole wyboru Sturm jest zaznaczone. Brakuje pominiętych częstotliwości pierwszych N postaci. Ta procedura jest dostępna w połączeniu z solwerami bezpośrednimi, jeśli jest stosowana metoda BLSI lub SI albo algorytm Lanczosa. Nie jest ona dostępna, jeśli jest stosowana podstawowa metoda redukcji lub dowolna metoda solwera iteracyjnego. Zdefiniuj N pierwszych sekwencyjnych postaci drgań własnych. Zostanie wykonana weryfikacja Sturm. Jeśli zostaną wykryte pominięte częstotliwości, zostanie wyświetlona ich liczba oraz monit. Jeśli udzielono instrukcji Tak proces iteracji będzie kontynuowany z ustaloną liczbą pominiętych postaci drgań własnych. Następnie weryfikacja Sturm zostanie powtórzona. Nie zbieżne postaci drgań własnych zostaną zapisane jako wynik końcowy i zostanie obliczony następny przypadek Anuluj iteracje będą kontynuowane, dopóki nie zostaną ustalone wszystkie pominięte częstotliwości. Ostrzeżenie zostanie zignorowane. Pole wyboru Sturm nie jest zaznaczone. Nie zostanie wykonana weryfikacja Sturm.
N	ω ^*	Nieaktywne (z powodu aktywne górnego limitu)	Analiza dostępna tylko w połączeniu z solwerami bezpośrednimi oraz metodą BLSI lub SI albo algorytmem Lanczosa. Nie jest ona dostępna, jeśli jest stosowana podstawowa metoda redukcji lub dowolna metoda solwera iteracyjnego. W momencie rozpoczęcia obliczeń jest wykonywana weryfikacja Sturm w celu uzyskania liczby częstotliwości N1 zawartych między zerem a górnym limitem: 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* Jeśli (N1 > N), zostanie wyświetlona liczba częstotliwości N1 oraz monit. Jeśli udzielono instrukcji Tak zostanie obliczone 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* Nie obliczenie zostaną przerwane. Jeśli (N1 <= N), zostanie obliczone 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* bez żadnych ostrzeżeń. W obu przypadkach można wyprowadzić większą liczbę zbieżnych par własnych niż N1, ale zostaną one zapisane jako wynik końcowy tylko wtedy, gdy 0 < ω₁ < ω₂ <... < ω_n₁ < ω^. Wszystkie zbieżne pary własne większe niż ω^, zostaną utracone.
N	Nieaktywne (z powodu aktywnego %masy)	Aktywne: 0<%masy<=100%	Dostępna w połączeniu ze wszystkimi metodami solwerów bezpośrednich. Nie jest dostępna w połączeniu z solwerem iteracyjnym. Jeśli %masy nie jest zadowalający, zostanie wyświetlony stosowny monit. Żadne korekty nie zostaną wprowadzone. W przeciwnym razie obliczenia będą wykonywane w taki sam sposób, jak w pierwszym przypadku.

Liczba postaci

Górne limity

%masy

Zachowanie programu

(nieaktywne)

Pole wyboru Sturm jest zaznaczone. Brakuje pominiętych częstotliwości pierwszych N postaci. Ta procedura jest dostępna w połączeniu z solwerami bezpośrednimi, jeśli jest stosowana metoda BLSI lub SI albo algorytm Lanczosa. Nie jest ona dostępna, jeśli jest stosowana podstawowa metoda redukcji lub dowolna metoda solwera iteracyjnego. Zdefiniuj N pierwszych sekwencyjnych postaci drgań własnych. Zostanie wykonana weryfikacja Sturm. Jeśli zostaną wykryte pominięte częstotliwości, zostanie wyświetlona ich liczba oraz monit. Jeśli udzielono instrukcji

Tak proces iteracji będzie kontynuowany z ustaloną liczbą pominiętych postaci drgań własnych. Następnie weryfikacja Sturm zostanie powtórzona.

Nie zbieżne postaci drgań własnych zostaną zapisane jako wynik końcowy i zostanie obliczony następny przypadek

Anuluj iteracje będą kontynuowane, dopóki nie zostaną ustalone wszystkie pominięte częstotliwości. Ostrzeżenie zostanie zignorowane.

Pole wyboru Sturm nie jest zaznaczone. Nie zostanie wykonana weryfikacja Sturm.

ω ^*

Nieaktywne (z powodu aktywne górnego limitu)

Analiza dostępna tylko w połączeniu z solwerami bezpośrednimi oraz metodą BLSI lub SI albo algorytmem Lanczosa. Nie jest ona dostępna, jeśli jest stosowana podstawowa metoda redukcji lub dowolna metoda solwera iteracyjnego.

W momencie rozpoczęcia obliczeń jest wykonywana weryfikacja Sturm w celu uzyskania liczby częstotliwości N1 zawartych między zerem a górnym limitem:

0 < ω₁ < ω₂ < … < ω_N₁ < ω^*

Jeśli (N1 > N), zostanie wyświetlona liczba częstotliwości N1 oraz monit. Jeśli udzielono instrukcji

Tak zostanie obliczone 0 < ω₁ < ω₂ < … < ω_N₁ < ω^*

Nie obliczenie zostaną przerwane.
Jeśli (N1 <= N), zostanie obliczone 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* bez żadnych ostrzeżeń.

W obu przypadkach można wyprowadzić większą liczbę zbieżnych par własnych niż N1, ale zostaną one zapisane jako wynik końcowy tylko wtedy, gdy 0 < ω₁ < ω₂ <... < ω_n₁ < ω^*.

Wszystkie zbieżne pary własne większe niż ω^*, zostaną utracone.

Nieaktywne (z powodu aktywnego %masy)

Aktywne:

0<%masy<=100%

Dostępna w połączeniu ze wszystkimi metodami solwerów bezpośrednich. Nie jest dostępna w połączeniu z solwerem iteracyjnym. Jeśli %masy nie jest zadowalający, zostanie wyświetlony stosowny monit. Żadne korekty nie zostaną wprowadzone. W przeciwnym razie obliczenia będą wykonywane w taki sam sposób, jak w pierwszym przypadku.

Sejsmiczna

Ten tryb jest dostępny tylko w połączeniu z solwerem skyline i bezpośrednim solwerem sparse.

W analizie sejsmicznej i spektralnej nie jest istotne, aby pary własne były ułożone w kolejności, ponieważ należy brać pod uwagę tylko te pary własne, które mają istotny wpływ na reakcję sejsmiczną (ponieważ mają znaczący współczynnik udziału masy). W związku z tym weryfikacja Sturm nie jest przeprowadzana.

Algorytm Lanczosa zapewnia zazwyczaj zbieżność znacznie większej liczby par własnych niż N par własnych w kolejności rosnącej sekwencyjnie. W razie konieczności przywrócenia pominiętych wartości własnych niezbędne jest uzyskanie znacznie większej liczby zbieżnych częstotliwości niż N pierwszych pożądanych częstotliwości. Typowa jest np. sytuacja, w której algorytm Lanczosa daje następujące zbieżne częstotliwości.

Jeśli użytkownik wymaga, aby pary własny były uporządkowane po kolei, uzyska tylko 10 pierwszych par własnych. Ostatnie 4 pary własne zostaną po prostu odrzucone, podobnie jak odpowiadający im wkład masy. Istotą proponowanego trybu „sejsmicznego” jest branie pod uwagę wszystkich zbieżnych par własnych (a nie tylko pierwszych sekwencyjnych par własnych). Suma mas jest wtedy większa niż w analizie „modalnej”.

Dostępne metody analizy: metoda Lanczosa.

Górne limity są ignorowane.

Bieżący procent masy jest wartością średnią M%x, M%y, M%z w przypadku problemów 3W i wartością minimalną spośród M%x, M%z w przypadku problemów 2W (M%x, M%y, M%z to bieżące sumy mas w poszczególnych kierunkach — x, y, z). Ta strategia jest uzasadniona tym, że zazwyczaj jest bardzo trudno uzyskać wystarczający procent mas w kierunku pionowym. Można sprawdzić procent masy dla każdego kierunku w ostatnich wynikach.

Npostaci	Górne limity	%masy	Zachowanie programu
N	Nieaktywne	Nieaktywne (0)	Oblicz N par własnych nieułożonych w kolejności. Nie zostanie wykonana weryfikacja Sturm. Liczba zbieżnych par własnych wynosi N.
N	Nieaktywne	Aktywne: 0<%masy<= 100%	N zostanie zignorowane. Obliczenia są kontynuowane dopóki aktualny procent masy nie jest mniejszy niż wymagany % masy lub pojawia się monit, aby zatrzymać obliczenia lub liczba zbieżnych par własnych osiąga maksymalną dostępną wartość. Te ustawienia wartości są definiowane wewnętrznie i w bieżącej wersji wynoszą 100. Po każdych 20 stopniach Lanczosa liczba zbieżnych par własnych jest ponownie obliczana i bieżący procent masy jest modyfikowany. Ostrzeżenie informuje o osiągniętym udziale procentowym masy. Jeśli udzielono instrukcji Tak, kontynuuje obliczenia podczas następnych 20 stopni Lanczosa i wyświetla ten komunikatu ponownie. Jeśli wymagany procent masy nie jest osiągnięty (liczba zbieżnych par własnych nie przekracza maksymalnej dostępnej wartości) Nie, zapisuje zbieżne pary własne jako końcowe wyniki, a następnie przekazuje je do następnego przypadku. Anuluj, ignoruje wszystkie ostrzeżenia w przyszłości i kontynuuje obliczenia.

Npostaci

Górne limity

%masy

Zachowanie programu

Nieaktywne

(0)

Oblicz N par własnych nieułożonych w kolejności. Nie zostanie wykonana weryfikacja Sturm. Liczba zbieżnych par własnych wynosi N.

Nieaktywne

Aktywne:

0<%masy<= 100%

N zostanie zignorowane. Obliczenia są kontynuowane dopóki aktualny procent masy nie jest mniejszy niż wymagany % masy lub pojawia się monit, aby zatrzymać obliczenia lub liczba zbieżnych par własnych osiąga maksymalną dostępną wartość. Te ustawienia wartości są definiowane wewnętrznie i w bieżącej wersji wynoszą 100.

Po każdych 20 stopniach Lanczosa liczba zbieżnych par własnych jest ponownie obliczana i bieżący procent masy jest modyfikowany. Ostrzeżenie informuje o osiągniętym udziale procentowym masy. Jeśli udzielono instrukcji

Tak, kontynuuje obliczenia podczas następnych 20 stopni Lanczosa i wyświetla ten komunikatu ponownie. Jeśli wymagany procent masy nie jest osiągnięty (liczba zbieżnych par własnych nie przekracza maksymalnej dostępnej wartości)

Nie, zapisuje zbieżne pary własne jako końcowe wyniki, a następnie przekazuje je do następnego przypadku.

Anuluj, ignoruje wszystkie ostrzeżenia w przyszłości i kontynuuje obliczenia.

Pseudo

Ten tryb jest dostępny dla obu solwerów: bezpośredniego i iteracyjnego. Jest to zalecane tylko w przypadku analizy sejsmicznej i spektralnej, gdy tryby modalny i sejsmiczny są zbyt czasochłonne. Tryby sejsmiczny i modalny używają trybów własnych jako wektorów bazy dla prezentowania odpowiedzi sejsmicznej i możliwe jest wymaganie bardzo dużej liczby trybów własnych, aby zapewnić wystarczającą suma mas dla niektórych trudnych problemów. W trybie pseudo ten pomysł jest odrzucany i generowany są przybliżenia Ritza do najniższych par własnych za pomocą wektorów Lanczosa dla bezpośrednich solwerów lub gradientów Ritza[8] i modyfikowanej metody Lanczosa dla solwerów iteracyjnych. Jest to bardziej efektywny sposób operacji w większości przypadków, ponieważ mniejsza liczba wektorów bazy jest wymagana, niż w trybie modalnym. Jest to pokazane przez E.L.Wilson [1-3]. Tryb pseudo jest podobny do wektorów Ritza zależnych od obciążenia, proponowanych w [1-3] i stosowanych w SAP2000. Należy zauważyć, że francuska norma PS-92 przyjmuje aplikacje podejść o naukowych podstawach w celu dodania systemów wektorów bazy do istniejących trybów własnych w celu zwiększenia sumy mas. Szczegóły podejścia trybu pseudo i jego efektywność są dostępne w dodatkach 3B i 3C.

Górne limity są ignorowane.

Bieżący procent masy jest zdefiniowany jako średnia wartość M%x, M%y, M%z dla problemów 3-D i jako minimalna wartość M%x, M%z dla problemów 2-d (M%x, M%y, M%z są bieżącą sumą mas dla kierunku osi x, y, z). Ta strategia ma uzasadnienie w tym, że zazwyczaj jest bardzo trudno uzyskać wystarczający procent mas w kierunku pionowym. Można sprawdzić procent masy dla każdego kierunku w ostatnich wynikach.

Npostaci	Górne limity	%masy	Zachowanie programu
N	Nieaktywne	Nieaktywne (0)	Dostępne zarówno dla solwerów iteracyjnych i bezpośrednich. Generowanie wektorów bazy N, aby zdefiniować pracę podprzestrzenną. Zapisz wektory bazy N do użycia z analizami sejsmiczną i spektralną. Taki reżim jest zalecany.
N	Nieaktywne	Aktywne: 0 < % masy <= 100%	Opcja jest dostępna tylko dla bezpośrednich solwerów Generowanie wektorów bazy N, aby zdefiniować pracę podprzestrzenną. Zapisz te wektory bazy, które wystarczą, aby wypełnić dany % masy. Liczba zapisanych wektorów bazy jest mniejsza niż N, jeśli %masy < 100%

Npostaci

Górne limity

%masy

Zachowanie programu

Nieaktywne

(0)

Dostępne zarówno dla solwerów iteracyjnych i bezpośrednich.

Generowanie wektorów bazy N, aby zdefiniować pracę podprzestrzenną. Zapisz wektory bazy N do użycia z analizami sejsmiczną i spektralną.

Taki reżim jest zalecany.

Nieaktywne

Aktywne:

0 < % masy <= 100%

Opcja jest dostępna tylko dla bezpośrednich solwerów

Generowanie wektorów bazy N, aby zdefiniować pracę podprzestrzenną. Zapisz te wektory bazy, które wystarczą, aby wypełnić dany % masy. Liczba zapisanych wektorów bazy jest mniejsza niż N,

jeśli %masy < 100%

3.6 Analiza spektralna

Metoda spektrów odpowiedzi jest stosowana dla analizy sejsmicznej i spektralnej. Metoda ta składa się z dekompozycji konstrukcji z wielokrotnych stopni swobody (MDOF) do systemu jednostopniowych oscylatorów swobody (SDOF). Odpowiedź dla każdego z tych niezależnych oscylatorów i statystycznej sumy ekstremalnej odpowiedzi dla każdego oscylatora jest obliczana przy pomocy SRSS, CQC, metody dziesięciu procent i podwójnej sumy [3, 21].

Tryby własne definiują system oscylatorów SDOF, gdy tryby modalne lub sejsmiczne są stosowane. Wektory bazowe trybu pseudo definiują ten system oscylatorów SDOF, gdy stosowany jest tryb pseudo (zobacz rozdział 3.5).

Wprowadzenie trybu pseudo wymaga nowego podejścia do oceny odpowiedzi dla każdego trybu. Klasyczne podejście jest następujące:

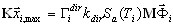( 3.1.1 )

gdzie K, M — macierze sztywności i masy, Γ — współczynnik uczestnictwa masy, S_a — przyspieszenie spektra, T — kropka, i — numer trybu, k — współczynnik skalowania spektrum, dir — indeks wprowadzonego kierunku ruchu sejsmicznego (dir = X, Y, Z), x — wektor przesunięcia dla maksymalnej reakcji trybu i.

Teraz, stosowane jest następujące (zobacz załącznik B):

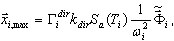( 3.1.2 )

gdzie 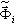oznacza wektor bazy (nie jest to konieczne dla 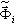, aby było dokładnym przybliżeniem 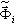— dokładny wektor własny 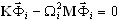, ω_i — przybliżenie dokładnego wektora własnego Ωi. Jest możliwe, aby pokazać, że (3.1.1) daje dokładnie takie samo rozwiązanie 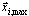jak (3.1.2), jeśli 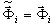(ωi = Ωi). Jednakże (3.1.2) ma zastosowanie nie tylko do bezpośrednich solwerów, ale także do solwerów iteracyjnych, ponieważ nie wymaga procedury rozwiązania odpowiadającej macierzy sztywności K. W ten sposób proces przebiega szybciej niż w przypadku (3.1.1) i możliwa jest bardziej bezpieczna kontrola wyników (suma sił 0 suma reakcji).

Niżej zaprezentowana formuła wyznaczana jest z (3.1.1)

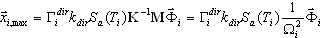( 3.1.3 )

Wektor odpowiedzi modalnej 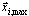opisuje odpowiedź ekstremalną odpowiedniego oscylatora SDOF. Następny krok powinien być przeznaczony do zdefiniowania ostatecznej odpowiedzi konstrukcji MDOF za pomocą średniej statystycznej pomiędzy trybami i między sejsmicznymi kierunkami wejściowymi.

Wcześniejsze wersje programu Robot umożliwiają przypisanie kilku statystycznie niezależnych sejsmicznych kierunków wejściowych własnych mnożników skali w jednym przypadku obciążenia. Statystyczna średnia między kierunkami jest wytwarzana przez sumę wartości bezwzględnych, a pierwiastek kwadratowy sumy kombinacji kwadratów w ramach każdego trybu. Odpowiednie opcje są zdefiniowane w Preferencjach zadania.

Opcja "suma wartości bezwzględnych" pozwala na następujące:

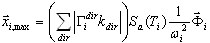( 3.1.4 )

Pierwiastek kwadratowy sumy opcji kwadratów powoduje uśrednienie 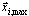odpowiadających sejsmicznych kierunków ruchu wejściowego, takiego jak .

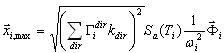( 3.1.5 )

Jest możliwe, aby pokazać, że każdy składnik 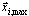jest kombinacją SRSS odpowiednich składników .

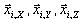gdzie i =1,2,..., N oznacza liczbę trybów lub trybów pseudo.

Kombinacja SRSS lub CQC między trybami (lub pseudo modami) jest stosowana w celu uzyskania ostatecznej odpowiedzi dla branej pod uwagę konstrukcji MDOF po tym, jak wektory średniej odpowiedzi modalnej 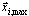zostały uzyskane, i =1,2,..., N.

Wektory modalnej średniej odpowiedzi 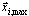, i =1,2,..., N, są takie same dla "sumy wartości bezwzględnych" i pierwiastka kwadratowego sumy opcji kwadratów, jeśli jeden kierunek wejścia sejsmicznego został zdefiniowany dla bieżącego przypadek obciążenia (na przykład Kx=Kz=0, Ky=1).

Robot (wersja 12.2 i nowsze) zapisuje powyższą procedurę uśredniania modalnych odpowiedzi między kierunkami wejść sejsmicznych, jednak pozwala na przeprowadzenie najlepszego podejścia. Zaleca się, aby zdefiniować pojedynczy wprowadzony kierunek sejsmiczny dla każdego przypadku obciążenia, a następnie zastosować kombinację SRSS między kierunkami (odpowiadającymi regulacjom amerykańskim) lub tak zwanym kombinacjom „Newmarka” (odpowiadającym francuskiej normie sejsmicznej PS-92 i Eurocode-8).

Teraz przedstawione zostaną nowe możliwości następujących typowych przykładów.

W tym przypadku (pojedynczy wprowadzony ruch sejsmiczny dla każdego przypadku obciążenia), typowe wartości mnożników skali będą równe

Kx=1; Ky=Kz=0 dla dir = X (przypadek obciążenia S_X)

Kx=0 Ky=1 Kz=0 dla dir = Y (przypadek obciążenia S_Y)

Kx=Ky=0; Kz=0.7 dla dir = Z (przypadek obciążenia S_Z; pionowe natężenie ruchu przyjmowane jest równe 2/3 natężenia ruch poziomego)

Trzy przypadki obciążeń są zdefiniowane dla każdego statystycznie niezależnego wprowadzonego sejsmicznego ruchu. Odpowiedź modalna dla każdego będzie taka sama jak (3.1.2) (i = 1,2,..., N; dir = X, Y, Z).

Następnie, konieczne jest zdefiniowanie współczynnika uśredniania dla wszystkich trybów w związku z każdym wprowadzonym sejsmicznym kierunkiem: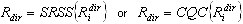

gdzie 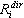— jakiś współczynnik (przesunięcie, siła, naprężenie,...) dla trybu i-tego ze względu na wprowadzony ruch sejsmiczny w kierunku dir, który odpowiada modalnej odpowiedzi 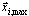(uzyskanej z (3.1.2);

Rdir jest wynikiem kombinacji SRSS lub CQC nad wszystkimi branymi pod uwagę trybami (pseudo modami).

Następnie, uśrednianie wszystkich aktywnych wprowadzonych kierunków sejsmicznych zgodnie z wybraną opcją jest wytwarzane.

Każda kombinacja SRSS:

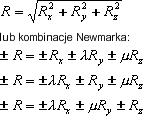
Opcje Analizy spektralnej umożliwiają definicję dowolnego spektrum wprowadzonego ruchu sejsmicznego.

3.7. Analiza sejsmiczna

Metoda spektrów odpowiedzi jest stosowana dla analizy sejsmicznej i spektralnej. Analiza sejsmiczna jest przeprowadzana w oparciu o analizę spektralną (patrz rozdział 3.6), jednak przyśpieszenia spektrów Sa = Sa (Ti) są generowane zgodnie z wybraną normą sejsmiczną, a nie są przypisywane przez użytkownika (jak jest to wykonywane dla analizy spektralnej).

Norma sejsmiczna UBC—97 jest dostępna w programie Robot (wersja 12.0 i późniejsze). Analiza spektrum odpowiedzi jest przeprowadzana zgodnie z rozdziałami 1631.5.1 — 1631.5.3 z Jednakowej normy budowlanej 1997. Jest możliwe, aby spełnić wymagania rozdziału 1631.5.4 ("Parametry odpowiedzi sprężystej mogą zostać zmniejszone...") za pomocą mechanizmów kombinacji programu Robot. Podstawowe składniki ścinające Vx, Vy, Vz, składniki momentu obrotu Mx, My i momentu skręcającego Mz (zakłada się, że oś OZ jest pionowa) — wszystkie są prezentowane w tabeli „Reakcje” w wierszu „Suma sił”, zarówno dla każdej odpowiedzi modalnej, jak kombinacji SRSS i CQC między trybami.

Następujące normy sejsmiczne są dostępne w programie:

UBC97
PS 69 R. 82
AFPS
PS 92
RPA 88
DM 16.1.96
EC 8
IBC 2000
P100 92
norma turecka
normy chińskie
norma argentyńska
EAK 2000.

3.8. Filtry selektywne

Tylko tryby, które mają relatywnie znaczący współczynnik uczestnictwa masy, mają znaczący wpływ na odpowiedź sejsmiczną konstrukcji. Dlatego, wystarczy wzięcie pod uwagę tylko tych trybów. Pozostałe tryby o małym współczynniku udziału masy mogą być ignorowane podczas analizy sejsmicznej. Liczba derywowanych trybów jest zwykle znacząco większa niż liczba wynikająca z oceny procentu masy. Dlatego miejsce na dysku i czas obliczeń może być zapisane, jeśli tylko tryby z istotnym współczynnikiem udziału masy są wybrane.

Dwie metody mogą być użyte.

Utwórz listę akceptowanych trybów dla każdego wprowadzonego kierunku sejsmicznego (przypadku sejsmicznego) na podstawie poprzednio uzyskanych wyników analizy modalnej
Przypisz limit wartości granicznej masy dla procentu masy modalnej (wszystkie tryby z procentem masy modalnej poniżej tego ograniczenia będą ignorowane).

Pierwszy sposób jest bardziej wydajny, chociaż wymaga uprzedniej analizy modalnej. Drugi sposób umożliwia zastosowanie filtrów w tym samym przebiegu z analizą spektralną i sejsmiczną, jednak zwykle zajmuje więcej miejsca na dysku i wiąże się z większym wysiłkiem obliczeniowym.

Rozważmy inny przykład. Wyniki analizy modalnej są przedstawione poniżej, w tabeli 3.1, gdzie przypadki sejsmiczne definiowane są w następujący sposób: Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) i Dir_Z (Kx=Ky=0; Kz=1)

Tablica 1

Liczba postaci	Udział mas UX (%)	Udział mas UY (%)	Udział mas UZ (%)	Kropka
1	0.05	12.01	0.004	0.803
2	67.43	0.06	0.005	0.705
3	0.002	0.08	0.07	0.686
4	0.001	0.008	0.009	0.650
5	25.4	0.07	2.06	0.590
6	0.09	68.5	5.05	0.540
7	0.08	10.3	0.06	0.490
8	0.07	0.06	0.56	0.460
9	0.05	0.07	30.56	0.420
10	0.08	0.06	0.25	0.380
11	0.06	0.01	26.7	0.270

Załóżmy, że należy wziąć pod uwagę wszystkie tryby ze współczynnikiem udziału masy większym niż jeden procent. Odpowiednie wartości udziału masy są podane w tabeli. Należy zwrócić uwagę, że jeśli wprowadzone kierunki sejsmiczne są przypisane jako (1 0 0) dla przypadku sejsmicznego_X, tryby z odpowiednimi wartościami udziału masy dla kierunków UY, UZ w ogóle nie uczestniczą w odpowiedzi sejsmicznej (zobacz rozdział 3.6):

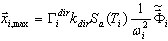
gdzie dir = X, Y, Z — dane wejściowe kierunku sejsmicznego; 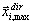—maksymalna odpowiedź dla i -trybu; — współczynnik udziału masy; Sa (Ti) — przyspieszenie spektrów; 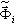— i-wektor własny lub wektor bazowy (w przypadku trybu pseudo). Mnożnik skalarny po prawej stronie powyższej formuły 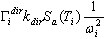definiuje udział i-trybu w odpowiedzi sejsmicznej dla kierunku dir. W tym przypadku, w którym Ky = Kz = 0, istotny udział zostanie wprowadzony przez tryby 2 i 5. Pozostałe tryby nie wpływają na odpowiedź sejsmiczną, ze względu na Kdir mnożnik zero (dir = Y, Z) i małe wartości uczestnictwa mas dla kierunku dir=X. Można pokazać — w ten sam sposób — że w przypadku Dir_Y wystarczy wziąć pod uwagę tryby 1, 6, 7, natomiast w przypadku Dir_Z — tryby: 5, 6, 9 11.

Dlatego za pomocą filtrów, program może brać pod uwagę tylko istotne tryby dla przypadku Dir_X uwzględnia — 2, dla Dir_Y 3 i dla Dir_Z 4. Ma to miejsce bez znaczącej utraty uczestnictwa masy. Należy zwrócić uwagę, że konieczne będzie zastosowanie trybu 11 dla każdego przypadku, jeśli nie zostaną użyte filtry.

To podejście umożliwia ograniczenie czasu obliczeń dla dużych problemów dynamicznych (oraz ilości wymaganego miejsca na dysku i ilości danych po obróbce) bez znacznego zmniejszenia dokładności wyników w porównaniu do tradycyjnej metody (gdy wybiórcze filtry nie są używane).

Na przykład duży problem PJG203 zawiera 34 266 równań (pasmo jest równe 990 po optymalizacji). Odpowiedni model ES jest prezentowany w załączniku 3D — patrz rys.A1. Miało być obliczonych 25 par własnych z rozłożoną macierzą mas i 3 przypadki sejsmiczne. Czas obliczania nadal osiąga około 50 godzin na Pentium Pro (64 MB pamięci RAM, 200MHZ). Wymagane miejsce na dysku twardym przekracza 1 GB. Ponadto, wyniknął problem z modułem wymiarowania stali, spowodowany zbyt małą ilością miejsca na dysku. (Aby obliczyć kombinacje SRSS i CQC, było konieczne, aby przechowywać dane z 25 trybów pomnożonych przez 3 przypadki sejsmiczne, składające się z dużej liczby stopni swobody dla wszystkich współczynników — przemieszczenia, wewnętrznych sił, naprężenia). Stosowanie filtrów selekcji umożliwia programowi skuteczne rozwiązanie tego problemu.

3.9 Analiza harmoniczna

Powstaje następująca definicja stałej reakcji konstrukcji przy działaniu pojedynczego harmonicznego obciążenia:

F (t) = F sin( ωt)

gdzie w stanowi pulsację obciążenia wymuszonego. Zachowanie konstrukcji jest opisane jako

(K — ω² M) X = F,

gdzie X — wartość amplitudy wektora przesunięcia.

3.10 Całkowanie równań ruchu

Metoda dekompozycji modalnej (superpozycja) będzie zrealizowana w programie Robot. Jest ona oparta na reprezentacji ruchu konstrukcji jako superpozycji ruchu trybów niezwiązanych. Stąd też metoda ta wymaga wyznaczenia wartości i wektorów własnych. Metoda Lanczosa jest zalecana do tego celu. Metoda dekompozycji modalnej stosuje zredukowane niesprzężone równania. Jest to odpowiednie podejście do analizowania dynamicznych odpowiedzi konstrukcji wystawionych na długotrwałe działanie obciążeń dynamicznych (na przykład, niestałe obciążenia spowodowane pracą wewnętrznego wyposażenia lub działaniem sejsmicznym). Tło matematyczne i cechy szczególne aplikacji są prezentowane w [3,4,6].

Równanie ruchu (bez tłumienia) można zapisać w postaci:

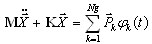(3.11.1)

gdzie Ng — liczba „grup obciążeń” φ_k(t) — w danym całkowaniu równań czasu k-tej grupy obciążeń.

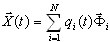(3.11.2)

gdzie 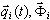— odpowiednio i-ta normalna współrzędna i tryb (wektor własny lub wektor Ritza). Zastąpienie (3.11.2) przez (3.11.1) i dodanie warunków tłumienia prowadzi do następujących równań trybów niezwiązanych [3,4,6]

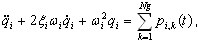(3.11.3)

gdzie 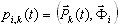, ξi — parametr tłumienia modalnego (zazwyczaj ξi: 0.05-0,2; gdy ξi = 1 oznacza to krytyczne tłumienie — ograniczenie między ruchem oscylacyjnym i ruchem aperiodycznym), ωi — naturalna częstotliwość wibracji (pulsacji), i=1,2,..., N

Każde z równań jest rozwiązane liczbowo. Metoda drugiego rzędu z automatycznym wyborem stopnia integracji jest zastosowana. Wynikły wektor przemieszczenia dla określonych punktów czasowych t = t1, t2,..., t5 wyznaczany jest przez zastąpienie qi (t5) w (3.11.2).

Metoda dekompozycji modalnej może być zastosowana dla analizy odpowiedzi sejsmicznej. W takim przypadku równanie ruchu ma następującą formę

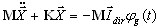
i odpowiednie równanie trybu niezwiązanego

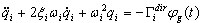(3.11.5)

gdzie 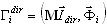— współczynnik udziału masy dla i-tego trybu i wprowadzonego kierunku sejsmicznego dir. Każdy tryb musi być znormalizowany w następujący sposób: 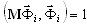. Na zakończenie wszystkie wyniki (przemieszczeń, prędkości, przyspieszeń, wewnętrznych sił, reakcji i inne) są przechowywane tylko dla określonych punktów czasu, t = t1 t2,..., t5. Wysoce wydajny post-procesor umożliwia przeprowadzenie analizy wyników całkowania równań ruchu zarówno w schemacie, jak i tabeli trybów. Tryb wykresu wyświetla wybrane współczynniki (przesunięcia, przyspieszenia, prędkości reakcji, sił ścinających, momentów zginających i innych) dla wybranych stopni swobody (DOFi przedstawia zdeformowany kształt konstrukcji w danym momencie. Tryb tabeli nie tylko pozwala zobaczyć odpowiednie wartości, lecz również umożliwia automatyczne wyszukiwanie wartości maksymalnych i minimalnych współczynników odpowiedzi na wszystkich zapisanych punktach czasu.

3.11. Analiza modalna biorąca pod uwagę siły statyczne

Liniowe niewielkie drgania w odniesieniu do stanu równowagi statycznej wymuszone przez dane obciążenie statyczne są brane pod uwagę. Statyczne siły są znane z tego, że mają wpływ na naturalne częstotliwości wibracji. Jeśli analiza modalna bierze pod uwagę siły statyczne, to bierze ona również pod uwagę ten wpływ, w przeciwieństwie do zwykłej analizy modalnej.

Pełne nieliniowe równania opisują ruch stanu względnej równowagi statycznej systemu, wywołanego przez dane obciążenia statyczne.

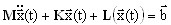(3.12.1)

gdzie M, K — macierze masy i sztywności, L (x (t)) — nieliniowe operatory, x (t), b — wektor przesunięcia i wektor obciążenia. Procedura linearyzacji składa się z następujących czynności:

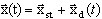(3.12.2)

gdzie x_st jest częścią wspólnego rozwiązania, które opisuje stan równowagi statycznej i x_d (t) jest wektorem małych dynamicznych przemieszczeń. Operator nieliniowy może być wyświetlony jako dekompozycja szeregu Taylora

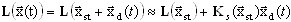(3.12.3)

gdzie 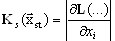— macierz sztywności naprężeniowej Jacobiego, uwzględniająca działanie sił statycznych. Wynika z tego poniższe:

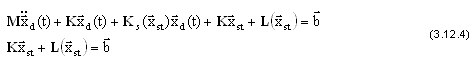
Pierwsze wyrażenie jest wynikiem linearyzacji odpowiednio małych dynamicznych przemieszczeń (uwaga: 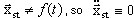), a drugie opisuje nieliniowy stanu równowagi statycznej. Dlatego, mały ruch dynamiczny w odniesieniu do stanu równowagi jest następujący:

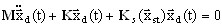(3.12.5)

Umożliwia to zastąpienie x_d (t) = Φ e^{i ω t}. Problem wartości własnych pochodzi z (3.12.5)

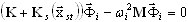(3.12.6)

gdzie ω_i — wartość własna; Φ_i — wektor własny.

Obliczenia wykonywane są w dwóch etapach:

Liniowej (3.12.7) lub nieliniowej (3.12.8) analizie statycznego stanu naprężenia—wymuszenia przyłożonego przez dane obciążenie statyczne
K x_st = b (3.12.7)

K x_st + L (x_st) = b, (3.11.8)

gdzie x_st — nieznany wektor statyczny, b — wektor danych sił statycznych (wektor obciążenia statycznego), K — macierz sztywności, L (x_st, b) — nieliniowy operator. Wektor obciążenia statycznego b może być rezultatem kombinacji kilku obciążeń statycznych. Powinien być tu zauważone, że liniowe podejście nie odpowiada dokładnie równaniu równowagi nieliniowej (3.11.8). Dlatego, wektor x_st w stanie równowagi statycznej jest wynikiem rozwiązania przybliżonego i macierz sztywności naprężeniowej K_s(x_st) zawiera błąd. Jeśli brana pod uwagę konstrukcja jest dostatecznie sztywna i nieliniowe efekty prawie się nie pojawiają, to takie przybliżenie wydaje się być poprawne. W przeciwnym razie, konieczne jest rozwiązanie tego problemu nieliniowego statycznego (3.11.8) (ta technika nie została opisana przez podręcznik). Oczywiście, liniowe podejście (3.2.17) jest szybsze niż nieliniowe (3.11.8). W przypadku podejścia liniowego okazuje się, że K_s(x_st) = G (x_st) = G, gdzie G to geometryczna macierz sztywności.
Analiza wartości własnych (3.12.6)
Dodatnie wartości ωi (ωi > 0) są znane z tego, że przedstawiają stały stan równowagi, wartości ujemne (ωi < 0) — niestałe, natomiast wartość zero (ωi =0) odpowiada brakowi stabilności (wyboczeniu).

Utrata dodatniej określoności macierzy K + K_s(x_st) oznacza, że obciążenie statyczne przekracza jego wartość krytyczną(wyboczeniową). Jest wydawane odpowiednie ostrzeżenie. Zbieżność zostanie utracona podczas uruchomienia nieliniowego problemu statycznego (3.11.8). Zaleca się, aby przerwać obliczenia, ponieważ następujące obliczenia są nadal pozbawione sensu.

Dla konstrukcji zawierających przewody i elementy ściskające-rozciągające dostępne jest tylko podejście nieliniowe.

Na przykład, weźmy pod uwagę następujące rysunki.

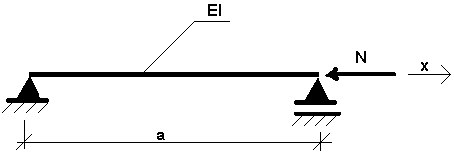
Rys. 3.11.1

Gdzie N — statyczne obciążenie. Poniższe wyrażenie opisuje zachowanie takiego systemu:

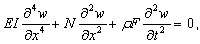( 3.11.9 )

gdzie: w — przemieszczenie zginające, ρ — gęstość materiału, F — przekrój poprzeczny obszaru.

Rozwiązanie będzie przeszukiwane jako

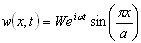( 3.11.10 )

Po zakończeniu substytucji (3.11.10) przez (3.11.9), następujące jest derywowane:

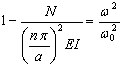, ( 3.11.11 )

gdzie — obciążenie wyboczeniowe, ω₀ — wartość własna dla N = 0 (wynik dla normalnej analizy modalnej). W końcu,

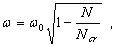( 3.11.12 )

gdzie ω — wartość własna dla systemu poddanego działaniu obciążenia statycznego N. Ten wynik jest prezentowany graficznie na rys. 3.11.2:

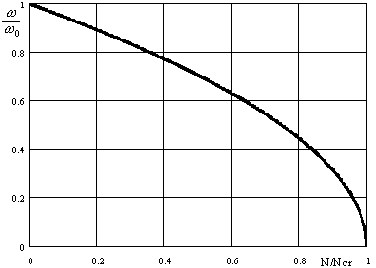
Rys. 3.11.2

Zależność ω = ω (λ), gdzie l jest parametrem obciążenia, dla rzeczywistej konstrukcji jest zwykle bardziej złożone niż reprezentowane przez wyrażenie (3.11.12) (zobacz [1,22]).

Załącznik 3A

Metody rozwiązania problemu własnego

Należy zrozumieć, że najlepsza uniwersalna metoda rozwiązania problemu własnego nie istnieje.

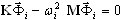, i=1,2,..., n (A1)

gdzie K to macierz sztywności, M to macierz masy, – tryb własny i ω_i — pulsacja. Dla większości problemów taka metoda będzie zawierać mniej zasobów (czas obliczeń i HD magazyn) niż jakakolwiek inna. Jednakże, opcja ta nie wyklucza różnych sytuacji w przypadku innych zadań. Aplikacja innej metody jest zalecana. Aktualna wersja programu Robot zawiera kilka metod rozwiązywania uogólnionego problemu własnego (A1). Każda z nich posiada swoje zalety i wady. Poniżej, istnieje kilka zaleceń, które mają być brane pod uwagę podczas wybierania metody analizy. Mamy nadzieję, że w większości przypadków będą prowadzić one do wymaganych wyników w najlepszy sposób.

Iteracja podprzestrzeni (SI) będzie zrealizowana dokładnie tak, jak opisano w [4], dlatego opis tej metody nie jest zawarty w tym miejscu.

Lanczos

Metoda Lanczosa [12,16,17] jest skutecznym rozbudowanym podejściem używanym do rozwiązywania dużych problemów wartości własnej (A1). Jest dostępna, gdy solwery bezpośrednie skyline lub sparse zostaną wybrane.

To podejście znajduje wymagane pierwsze wartości własne n i tryby własne z dowolną żądaną dokładność. Im większa liczba wymaganych par własnych jest uzyskiwana, tym bardziej zalecana jest metoda Lanczosa. Jednak podejście to wiąże się z kilkoma ograniczeniami.

Trzy-diagonalna macierz T nie powinna być rozkładana. Analiza konstrukcji nie jest możliwa, gdy składa się ona z dwóch lub więcej niepołączonych podkonstrukcji. W takim przypadku, każda podkonstrukcja jest analizowana niezależnie lub stosowane jest inne podejście (na przykład blokowa iteracja podprzestrzeni (BLSI) lub metoda redukcji bazy).

Macierz mas M powinna być traktowana jako skupiona z rotacją lub spójna.

Gęstość zero nie jest dopuszczalna.

Metoda Lanczosa stosuje redukcję macierzy-trzy diagonalnej T

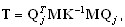, (A2)

gdzie Q_j = {q1, q2, … , qj} — macierz prostokątna Neq x j, Neq jest liczbą równań, j — liczbą kroków „Lanczosa”, qj — j-ty wektor Lanczosa. Wyrażenie

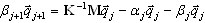(A3)

generuje następny wektor Lanczosa qj + 1 i definiuje bieżącą linię macierzy T

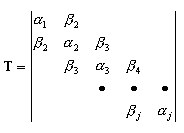
Oznacza to, że poniższy zmniejszony problem własny jest uzyskiwany:

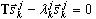, k=1,2,..., j (A4)

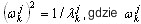jest j—tym przybliżeniem do ω_k, k=1,2,..., n, n jest wymaganą liczbą par własnych. Algorytm będzie nadal obliczał (aby zwiększyć j — liczbę kroków Lanczosa), aż osiągnięta zostanie wymagana dokładność dla wszystkich wymaganych wartości własnych.

Wybiórcza procedura ortogonalizacji wspiera wymagany poziom ortogonalności między wektorami Lanczosa qj, co zapewnia bezpieczeństwo i numeryczną stabilność procesu obliczeniowego. Należy zastosować ekonomiczną metodę, aby zapewnić wybiórczą ortogonalizację i rozwiązać problem zredukowanej wartości własnej (A4) przez podwójną iterację QR z przesunięciami.

Źródłowe wektory własne są określane według następującego wzoru

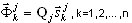(A5)

Szczegóły są prezentowane w [12,16,17].

Metoda redukcji bazy

Ta metoda [4, 5] jest znana jako poprawiona metoda Rayleigha-Ritza [4]. W [5] takiej metodzie odrębna odmiana metody Bubnowa-Galerkina jest prezentowana. Algorytm ten umożliwia uzyskanie wartości przybliżonych pierwszych kilku par własnych, jeśli znane są pewne informacje na ich temat. Metoda wymaga zdefiniowania stopni swobody typu „master” (MDOF — „master degree of freedom”) w celu uzyskania układu zredukowanego. Dlatego proces tworzenia zmniejszonego modelu mogą być kontrolowany. Jest to potężne narzędzie dla tych, którzy posiadają doświadczenie w dynamicznej analizie konstrukcji i pracują z tego samego typu konstrukcjami, których zachowanie jest znane. Ta metoda umożliwia wykluczenie niepożądanych stopni swobody (DOF) ze zredukowanego modelu i zredukowanie początkowo złożonego problemu z dużą liczbą stopni swobody do formy zredukowanej. Jest to osiągane przy znacząco zredukowanej liczbie stopni swobody. Doświadczenie dotyczące analizy dynamicznej konstrukcji pokazuje, że niektóre problemy mogą zostać wykryte przez użytkownika, gdy automatyczna metoda redukcji (BLSI, SI i Lanczos są brane pod uwagę) prowadzi do bardzo złożonych obliczeń. Na przykład, tryby lokalnego drgania pojedynczych prętów mogą prowadzić do poważnych problemów, ponieważ proces obliczania szuka par własnych automatycznie bez żadnego wyboru. Tak powinno być dla większości przypadków w rzeczywistych konstrukcjach. W przeciwnym wypadku lokalne drgania zostaną ograniczone przez niektóre więzy, które nie są brane pod uwagę w modelu FEM, lub ich udział nie będzie konieczny w całkowitym ruchu systemu. Zazwyczaj procent masy jest bardzo mały w takim lokalnym drganiu. Użycie dokładnych metod, w tym przypadku będzie prowadzić do wyżej wspomnianych problemów. Natomiast zastosowanie przybliżonej metody redukcji podstawowej może znacznie uprościć proces obliczeniowy.

Ta metoda ma następujące ograniczenia.

Użytkownik ma do przypisania MDOF: główne węzły i główne kierunki. Zakłada się, że tylko przemieszczenia (a nie obroty) mogą być przyjęte jako stopnie swobody typu „master”.

Algorytm jest stosowany dla dowolnego typu macierzy mas; jednakże skupiona macierz mas bez rotacji jest najbardziej korzystna pod względem czasu obliczeń.

Sprawdzenie sekwencji Sturma nie jest dostępne. Istnieje tylko jeden sposób sprawdzenia zbieżności. Zwiększenie liczby MDOF (przypisanie dodatkowych głównych węzłów i głównych kierunków), rozwiązanie tego problemu jeszcze raz i porównanie wartości własnych.

Taka metoda przekształca źródłowy duży problem wartości własnej dla

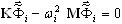(A6)

modelu FEM (A1) w problem wartości własnej dla zredukowanego modelu

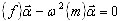(A7)

gdzie {f} — macierz wpływu, {m} — uogólniona macierz mas dla zredukowanego modelu,

(A8)

gdzie n to liczba stopni swobody zredukowanego modelu. Podstawą dla takich przekształceń jest rozwiązanie statyczne uzyskane dla odpowiednich stanów jednostkowych: jednostkowe siły węzłowe są stosowane konsekwentnie w każdym węźle głównym, w wybranym kierunku głównym. Statyczny problem dużej skali został rozwiązany dla n prawych stron:

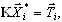i = 1, 2,..., n (A9)

gdzie Ti — wektor obciążenia, który odpowiada i — jednostkowemu obciążeniu. Użytkownik ma do przypisania główne węzły i główne kierunki. Wszystkie wymagane operacje będą wykonywane przez program.

Zredukowana wartość własna problemu została rozwiązana przez metodę Jacobiego, co prowadzi do przybliżania częstotliwości ω_i i trybów 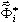, i=1,2,..., n. Szczegóły tego podejścia są prezentowane w [5].

Metoda blokowej iteracji podprzestrzennej

Metoda blokowej iteracji podprzestrzennej (BLSI) rozwiązuje ogólny problem wartości własnej (A1). Jest on dostępny dla bezpośrednich solwerów skyline i sparse. Jest to potężnie rozbudowane podejście. Ta metoda jest zdecydowanie zalecane w przypadku, gdy duży problem pojawia się, i jest ona niezbędna, aby uzyskać większą liczbę par własnych (więcej niż 10). BLSI może być zastosowana do analizy oddzielnych konstrukcji. Podczas analizy modalnej są dostępne wszystkie typy macierzy mas (skupiona bez rotacji, skupiona z rotacjami i rozłożona). Obszar aplikacji tego podejścia jest ograniczony przez tryb modalny. Tryb sejsmiczny i tryb pseudo są nadal dostępne, jeśli jest wybrana opcja Lanczosa.

W sekwencji Sturma wykonywane jest sprawdzenie, aby wykryć pominięte wartości własne. BLSI kontroluje ciągłość zbieżnych wartości własnych. Nieciągłość zbieżnych wartości własnych oznacza obecność pominiętych wartości własnych. Jednak ciągłość zbieżnych wartości własnych nie zapewnia ścisłej pewności, że brakuje pominiętych wartości własnych. Niemniej, wyniki wielu obliczeń wskazują, że w większości przypadków sprawdzenie sekwencją Sturma nie wykrywa pominiętych wartości własnych, podczas gdy BLSI zapewnia ciągłość zbieżności. Dużą zaletą tej metody jest możliwość uniknięcia czasochłonnej procedury sprawdzania Sturma, jeśli pełna gwarancja brakujących i pominiętych wartości własnych nie jest wymagane. Jeśli nieciągłość zbieżnych wartości własnych pojawia się, wyświetli się następujący komunikat (zobacz rys. A1).

Główna idea metody BLSI [1-3] składa się z jednoczesnych iteracji wektorów w podprzestrzeni stałego rozmiaru. Każdy zbieżny wektor jest usuwany z podprzestrzeni pracy (blokowej) i w jego miejsce dodawany jest nowy wektor początkowy Ortogonalność zbieżnych wektorów jest zapewniana na każdym kroku iteracji.

Zastosowanie procedury przyśpieszenia przesunięcia [1,4] jest zalecane podczas analizy modalnej, gdy występuje wolna zbieżność.

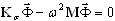, (A10)

gdzie K_σ= K — σ M, σ — wartość przesunięcia. Na początku analizy jest założone, że σ = 0. Aktualizacja automatyczna wartości przesunięcia jest zapewniana, jeśli nowe zbieżne wartości własne nie pojawią się podczas zaakceptowanej liczby kroków kontroli iteracyjnej. Na przykład, zaakceptujmy liczbę kroków kontroli równą 5. Następnie 5 zbieżnych wartości własnych pojawi się po 4 iteracji. Wartość przesunięcia pozostaje σ = 0. W następnym kroku iteracji 3 wartości własne są zbieżne. Wartość przesunięcia pozostaje σ = 0. Następnie, w ciągu 5 kroków iteracji nie występuje zbieżność między trybami własnymi. Algorytm znowu wykrywa „wolną zbieżność”, przyjmuje σ = ω₈ ², aktualizuje K_σ = K - σ M i faktoryzuje zaktualizowaną macierz przesunięcia K_σ. Następnie po kroku 2 iteracji zbiegają się 2 tryby własne. Wartość przesunięcia pozostaje ω₈ ². Następnie podczas następujących 5 kroków iteracji nie zbiegają się żadne wartości własne. Algorytm ponownie wykrywa „wolną zbieżność” i wymaga ω₁₀ ², aktualizuje K_σ = K - σ M i faktoryzuje aktualizowaną macierz przesunięcia K_σ.

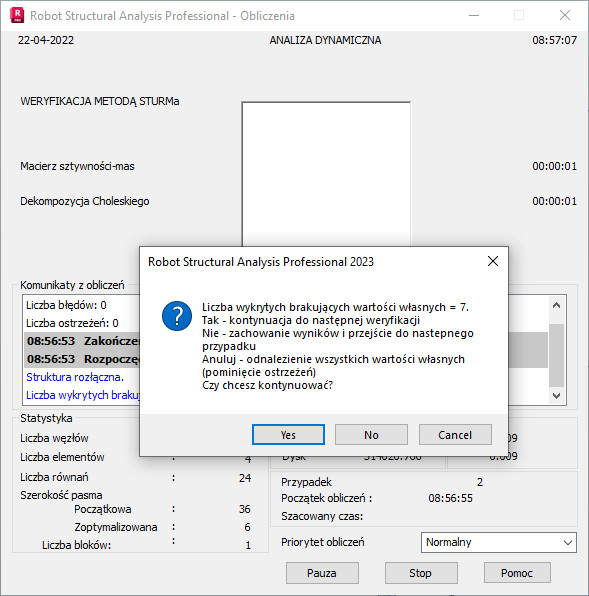
Rys. Nieciągłość A1 zbieżnych wartości własnych jest wykrywana podczas uruchamiania BLSI.

Jeśli udzielono instrukcji

Tak, obliczenia są kontynuowane aż do pojawienia się następnych zbieżnych wartości własnych. Potem, następna weryfikacja będzie przeprowadzona.
Nie, wyniki zostaną zapisane i obliczenia przejdą do następnego przypadku.
Anuluj, obliczenia będą kontynuowane, dopóki pełna ciągłość zbieżnych wartości własnych jest nie zostanie zapewniona. Ostrzeżenie będzie ignorowane.

To nie są wszystkie zalecenia. Można albo zastosować, albo nie stosować przyspieszeń przesunięcia. Należy pamiętać, że zastosowanie odpowiedniego przesunięcia pozwala skutecznie przyspieszyć zbieżność. W przeciwnym razie każda faktoryzacja aktualizowanej macierzy K_σ może być czasochłonną procedurą, szczególnie przy dużym problemie. Dlatego ostateczna decyzja o aplikacji przesunięcia powinna być podejmowana w oparciu o doświadczenie i intuicję użytkownika.

Poniższy przykład przedstawia korzyści z aplikacji przesunięcia. Model obliczeniowy jest pokazany na rys. A2. Istnieje 50 trybów własnych wyodrębnionych przez BLSI. Solwer skyline jest wybrany. Zostanie przyjęta tolerancja 1.0e-09. Okaże się, że zbieżność rozpoczynająca się od 38. trybu jest nadal tak wolna, że w ciągu 20 minut obliczeń nie zostały uzyskane żadne wyniki. Kiedy przyspieszenie przesunięcia (aktualizacja przyśpieszenia została zaakceptowana dla każdego z 5 nieprzekształconych kroków iteracji) zostało włączone, czas obliczeń nadal liczy do 50 sekund. Oczywiście jest możliwe, aby przedstawić wiele przykładów, w których aplikacja przesunięcia zmniejsza liczbę iteracji, ale zwiększa czas obliczeń. Zalecamy uruchomienie przyspieszenia przesunięcia, gdy konwencjonalne podejście (przesunięcie jest wyłączone) powoduje dużą liczbę iteracji na niektórych etapach przebiegu BLSI.

Rys. A2 Przestrzenna konstrukcja ramy

Zmodyfikowana metoda Lanczosa

Jest to korekta metody Lanczosa w pseudo modzie do solwera iteracyjnego. Zwykle metoda Lanczosa wymaga faktoryzacji macierzy sztywności (zobacz A3). Jednak w przypadku dużych problemów faktoryzacja macierzy sztywności jest nadal bardzo czasochłonna. W przypadku dużych problemów (ponad 100 000 równań), oprócz tego, że faktoryzacja macierzy sztywności wymaga skomplikowanych obliczeń, to rozwiązanie zestawu równań odpowiednio faktoryzowanej macierzy jest kosztowne.

Zmodyfikowana metoda Lanczosa bazuje na podejściu iteracyjnym. W ten sposób unika się przechowywania, składania i faktoryzowania dużych macierzy sztywności. Ocena każdego wektora Lanczosa wymaga mniej więcej tyle wysiłku obliczeniowego ile rozwiązanie statycznego problemu z pojedynczą prawą stroną. W odniesieniu do trybu pseudo, zmniejsza ona wymagana liczby wektorów Lanczosa w porównaniu do modalnej, która jest stosowana podczas uruchamiania zmodyfikowanej metody Lanczosa.

Solwer iteracyjny AEBEIS (zobacz rozdział [7, 8]) zostanie zastosowany do generowania wektorów Lanczosa. Zalecane jest użycie techniki ICCF (niekompletna faktoryzacja Choleskiego) dla obu wielopoziomowych agregacyjnych przygotowań wstępnych [7,8,18—20] i zwykłych nie wielopoziomowych. Zapewnia ona szybkie operacje podczas ewaluacji produktu macierzy—wektora i szybką rozdzielczość odpowiednich uwarunkowań wstępnych. Powinno zostać zanotowane, że tolerancja przyjęta dla solwera iteracyjnego (Preferencje zadania > Analiza konstrukcji > Parametry) określa dokładność oceny wektorów Lanczosa. Zazwyczaj jest to wystarczające, aby zaakceptować 1.0e—04. Im większa liczba trybów będzie brana pod uwagę, tym bliżej niskie wektory Ritza będą się znajdować do odpowiednich trybów własnych i pełniejsza suma mas modalnych zostanie osiągnięta.

Metoda gradientów sprzężonych (PCG)

metoda PCG [9—13] jest zalecana dla definicji małej liczby trybów własnych w trybie modalnym podczas jest zastosowany solwer iteracyjny. Może okazać się ona bardzo przydatna dla przypisywania obciążenia wiatrem lub do sprawdzania kilka niskich trybów uzyskanych przez metodę PCG_Ritz. Wszystkie typy warunkowania wstępnego (zobacz Narzędzia > Preferencje zadania > Iteracyjne > Parametry) zdefiniowane dla analizy statycznej, są dostępne. Mogą być używane wszystkie typy macierzy mas (rozłożone, skupione z rotacjami i skupione bez rotacji).

Metoda gradientów sprężonych jest oparta na bezpośredniej minimalizacji ilorazu Rayleigha

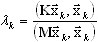(A11)

za pomocą podejścia gradientowego, gdzie: K — liczba iteracji, λ_k — odpowiadające przybliżenie wartości własnej. Podejście gradientowe wyszukuje takich wartości parametru α_k, które zapewniają minimalną wartość λk z (A11):

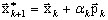(A12)

gdzie p_k jest wektorem sprzężonego kierunku. Wyszukiwanie odpowiedniej wartości α_k [zobacz 9—13] powoduje:

Warunkowanie wstępne B jest stosowane w celu przyspieszenia zbieżności

B z_{k + 1} = r_{k + 1} — > z_{k + 1} (A13)

Gradient jest zdefiniowany jako

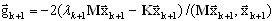(A14)

Nowy kierunek sprzężony zdefiniowany jest jako

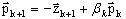(A15)

gdzie: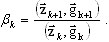

Iteracje są wykonywane aż do

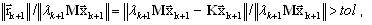(A16)

gdzie tol oznacza wymaganą tolerancję. Zazwyczaj tol = 1.0e—02 zapewnia bardzo dobrą dokładność dla celów inżynieryjnych. Należy pamiętać, że współczynnik zbieżności (A16) jest obliczany wg bardzo wymagającej normy (patrz część o dokładności obliczeń). Tolerancja wspomniana powyżej zapewnia dokładność wartości własnej nie mniejszą niż 1.0e—04.

Gdy pierwsza para własna jest zbieżna, jest ona zapisywana jako wynik końcowy i iteracja rozpoczyna się, aby obliczyć następną. Procedura ortogonalizacji uprzednio zdefiniowanych wektorów własnych na każdym kroku iteracji jest używana, aby uniknąć podwajania par własnych. Taki proces jest stosowany do czasu, aż wszystkie żądane pary własne zostaną uzyskane.

Najbardziej wydajnym sposobem przyspieszenia zbieżności dla PCG jest zastosowanie dobrego uwarunkowania wstępnego. Wszystkie typy uwarunkowania wstępnego przedstawione w iteracyjnym solwerze są dostępne dla metody PCG. Jest zalecane, aby zastosować wielopoziomowe ścisłe uwarunkowania wstępne [18—20] lub nie wielopoziomowe uwarunkowania wstępne z ICCF [9—12] wygładzające z solwera AEBEIS [7, 8].

Metoda Ritz—gradient (PCG_Ritz)

Metoda PCG_Ritz [8] jest szybką metodą definicji zestawu wektorów Ritza w pseudo modzie gdy jest wybrany solwer iteracyjny. Takie podejście może być bardzo owocne dla analizy sejsmicznej i spektralnej dla konstrukcji średniej wielkości, w tym (10 000 — 60,000) równań.

Jest ono oparte na generowaniu systemu ortogonalnego wektorów bazy. Podejście gradientowe z wielopoziomowym agregacyjnym uwarunkowaniem wstępnym w oparciu o technikę „element po elemencie” jest stosowane w celu zminimalizowania ilorazu Rayleigha dla każdego etapu przygotowania wektora bazowego. Zapewnia to rozwój wynikającego wektora bazy w kierunku najniższego trybu własnego bez agregacji i rozkładu macierzy sztywności o dużej skali. Taka metoda jest często bardziej efektywne dla analizy odpowiedzi dynamicznej w porównaniu do klasycznej metody modalnej superpozycji, szczególnie w przypadku analizy odpowiedzi sejsmicznej. Proponowana metoda umożliwia zastosowanie dowolnych typów elementów skończonych z powodu podejścia agregacyjnego i zapewnia szybkie rozwiązanie i niedrogie wymagania dotyczące pojemności dysku, spowodowane użyciem EBE. Metoda ta jest szczególnie skuteczna, gdy używana jest rozłożona macierz mas.

Dana wartość własna problemu jest następująca:

Kφ — λM φ = 0 (A17)

gdzie K, M to odpowiednio macierz sztywności i macierz mas, φ — wektor własny, a λ —wartość własna. Procedura rozwoju zestawu wektorów bazy x0, x1,..., xn ku najniższemu trybowi własnemu zostanie opisana. To podejście gradienta uwarunkowania wstępnego jest stosowane, aby zminimalizować iloraz Rayleigha

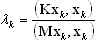(A18)

gdzie 0 ≤ k ≤ n, k jest numerem stopnia rozwoju; n + 1 oznacza liczbę wektorów podstawowych, które definiują rozmiar rozpiętości podprzestrzeni należącej do (x0, x1,..., xn); n + 1 < < N, gdzie N to liczba stopni swobody dla rozwiązywanego problemu (A17). Bardzo często okazuje się, że problem wartości własnej posiada nieprawidłowe uwarunkowania wstępne. W takim przypadku rozwój wynikającego wektora bazy xk do najniższego trybu własnego będzie bardzo mały. Ten operator uwarunkowania wstępnego B stosowany jest, aby poprawić taką sytuację. Wyrażenie B z_k = r_k — > z_k oznacza rozwiązanie danego zestawu równań odpowiedniego wektora zk, gdzie B jest operator uwarunkowań wstępnych i r_k = Kx _k — λ_k M x_k jest odpowiednim wektorem residualnym.

Wektory bazy spełniają następujące warunki ortogonaliczności:

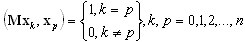(A19)

Źródło dużych problemów własnych (A17) jest redukowane do problemu własnego podprzestrzeni.

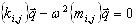(A20)

Macierze rzutowania podprzestrzeni są zdefiniowane jako {k_ij}= {Kx_i, x_j}i {m_ij}= {Mx_i, x_j}= U, gdzie U jest macierzą jednostkową.

Wektory Ritza v₁, v₂,..., v_{n + 1} dla pochodnych wektorów bazy x0, x1,..., xn i odpowiednie przybliżenia częstotliwości ω₁, ω₂,..., ω_{n + 1} są stosowane dla superpozycji odpowiedzi konstrukcji dynamicznej.

Procedura dla rozwoju wektorów bazy x_k, k = 0, 1,..., n do najniższego trybu własnego jest bardzo zbliżona do odpowiedniego kroku gradientu uwarunkowań wstępnych metody iteracji dla rozwiązania problemu własnego. Wiadomo, że zbieżność metody iteracyjnej uwarunkowań wstępnych zależy znacząco od właściwości operatora uwarunkowań wstępnych B. Operator ten powinien być określony dodatnio; pozwoli to na niedrogie rozwiązanie B z_{k + 1} = r_{k + 1} i spełnia numer warunkuC ( B^—1 K) — > 1 w najlepszy możliwy sposób.

Ostatnie wymaganie w przypadku metody Ritz-gradient zapewnia dobre przybliżenie niskiej część trybów własnych.

Taka metoda jest dostępna tylko dla powtarzającego się wielopoziomowego podejścia iteracyjnego, które zapewnia wysoką jakość uwarunkowania wstępnego Używane są obie techniki warunkowania wstępnego EBE (element po elemencie) i ICCF są . Jakość wektorów Ritza wygenerowanych w taki sposób zależy znacząco od właściwości operatora uwarunkowań wstępnych B (zobacz A13 i [8]). Ponieważ model poziomu zgrubnego dobrze przybliża tryb niskich drgań, wektory Ritza na wysokim poziomie są dobrym przybliżeniem odpowiednich wektorów własnych (zobacz [8]). Dlatego, jakość wyników uzyskanych za pomocą metody, zależy od możliwości modelu poziomu zgrubnego, aby zachować podobieństwo do danego modelu FEM (tak zwany wysoki poziom). Zwykle pojedynczy poziom agregacji zapewnia dobry poziom przybliżenia. Gdy liczba poziomów agregacji jest większa niż jeden, jakość wyników nie jest gwarantowana. Jest to główne ograniczenie dla zastosowania tej metody dla analizy dużych problemów, gdy liczba równań przekracza ~ 60000.

Jeśli macierz uwarunkowań wstępnych B = K (poziom zgrubny jest identyczny z wysokim poziomie), proponowana metoda Ritz-gradient przechodzi dokładnie do metody Lanczosa(zobacz [8]). Tło matematyczne jest prezentowany w [8].

Analiza modalna — dokładność obliczeń

Uogólniony problem wartości własnej zdefiniowany jest jako

Kφ — λM φ = 0 (A17)

gdzie K, M to odpowiednio macierz sztywności i macierz mas, {φ, λ} — pary własne (tryb naturalnych wibracji i wartości własnej). Definiowanie są dwa typy wektorów rezydualnych:

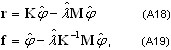
gdzie {φ, λ} są rzeczywiście obliczanymi parami własnymi, które zawierają niektóre błędy obliczeniowe. Pierwsze wyrażenie definiuje wektor rezydualny w odniesieniu do sił, a drugie — w odniesieniu do przemieszczeń.

Cztery różne kryteria są używane do oszacowania błędu obliczeniowego wektorów własnych.

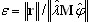. Jest to bardzo sztywne kryterium. Zazwyczaj ε ≤ 0,01 oznacza, że pierwsze cztery cyfr wartości własnej definiowane są dokładnie. Jest on stosowane tylko dla PCG, gdy wybrany jest solwer iteracyjny.
e = (r, φ). Jest to nieco bardziej rozmyte kryterium niż poprzednie. Jest ono stosowane w przypadku modyfikowanej metody Lanczosa, gdy solwer iteracyjny jest wybrany.
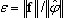. Jest to miękkie kryterium, ponieważ zbieżność przemieszczenia w danym wykonaniu FEM jest zazwyczaj szybsza niż zbieżność sił wewnętrznych. Jest ono używane dla BLSI, SI i Lanczosa, gdy bezpośrednie solwery skyline lub sparse są wybrane.
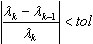gdzie λk, λk—1 — dwie kolejne wartości własne na k-tym i k-1 kroku iteracji, a tol oznacza tolerancję dla wartości własnych, przyjmowaną w oknie dialogowym Parametry analizy modalnej. Jest ona używana jako kryterium pośrednie podczas stosowania następujących metod: BLSI, SI i Lanczos (bezpośrednie solwery skyline lub sparse) w trybie modalnym. Takie kryteria nie jest odporne, jednak jest bardzo szybkie. Zastosowanie (4) pozwala znacząco zredukować czas obliczeń dla metod: BLSI, SI, Lanczosa, zwłaszcza w przypadku problemów o dużej skali. Gdy analiza wartości własnej jest zakończona, kryterium (3) jest stosowane jako końcowa weryfikacja dokładności. Użytkownik powinien spojrzeć na kolumnę "Dokładność" w tabeli, gdzie wartość 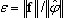jest wyświetlona. Jeśli spełniona jest niewystarczająca dokładność dla trybu własnego, konieczne jest, aby powtórzyć wartość własną analizy z większą tolerancję dla wartości własnej tol.

Poniższa tabela podsumowuje uwagi, wspomniane powyżej. Symbol N/A oznacza, że nie zostanie wykonana stosowna kontrola zbieżności. Wyniki końcowej weryfikacji pobierane są tylko raz i są prezentowane w kolumnie "Dokładność" w tabeli. Kontrola zbieżności podczas obliczeń jest wykonywana kilkukrotnie.

	Solwery bezpośrednie	Solwer iteracyjny
Typ kryterium	BLSI, SI, Metoda Lanczosa	Metoda redukcji bazy	Zmodyfikowany algorytm Lanczosa	PCG_Ritz	PCG
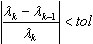
Podczas obliczeń		Brak	Brak	Brak
Weryfikacja końcowa		Brak	e = (r, j)	Brak

Solwery bezpośrednie

Solwer iteracyjny

Typ kryterium

BLSI,

SI,

Metoda Lanczosa

Metoda redukcji bazy

Zmodyfikowany algorytm Lanczosa

PCG_Ritz

PCG

Podczas obliczeń

Brak

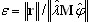
Weryfikacja końcowa

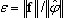
Brak

e = (r, j)

Brak

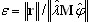
Należy odnotować, że metoda Lanczosa dla trybu sejsmicznego prowadzi do kontroli zbieżności 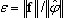przez każdy z 20 kroków Lanczosa. Metoda redukcji bazy i metoda PCG_Ritz są metodami Ritza. Ponieważ nie jest to podejście iteracyjne, weryfikacji dokładności nie jest wykonywane.

Jeśli dokładność niektórych trybów po obliczeniu wydaje się być niewystarczająca, konieczne jest następujące:

Solwery bezpośrednie	Solwer iteracyjny
BLSI, SI, Metoda Lanczosa — tryb modalny	Metoda redukcji bazy	Zmodyfikowany algorytm Lanczosa	PCG_Ritz	PCG
Zmniejszenie tolerancji w oknie dialogowym Parametry analizy modalnej	Zwiększenie liczby węzłów bazowych i kierunków bazowych	Zwiększenie liczby postaci Zmniejszenie tolerancji w oknie dialogowym Parametry solwera iteracyjnego	Zwiększenie liczby postaci Zmniejszenie liczy poziomów agregracji Zwiększenie liczby iteracji wewnętrznych	Zmniejszenie wartości tol w oknie dialogowym Parametry analizy modalnej

Solwery bezpośrednie

Solwer iteracyjny

BLSI,

SI,

Metoda Lanczosa — tryb modalny

Metoda redukcji bazy

Zmodyfikowany algorytm Lanczosa

PCG_Ritz

PCG

Zmniejszenie tolerancji w oknie dialogowym Parametry analizy modalnej

Zwiększenie liczby węzłów bazowych i kierunków bazowych

Zwiększenie liczby postaci

Zmniejszenie tolerancji w oknie dialogowym Parametry solwera iteracyjnego

Zwiększenie liczby postaci

Zmniejszenie liczy poziomów agregracji

Zwiększenie liczby iteracji wewnętrznych

Zmniejszenie wartości tol w oknie dialogowym Parametry analizy modalnej

Załącznik 3B

W podejściu pseudo

Równania źródła ruchu dla obciążeń sejsmicznych przybierają następującą formę:

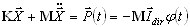(B1)

K, M — macierze sztywności i mas;

I dir — wektor jednostki kierunku; φ (t) — analiza czasowa dla przyśpieszenia ziemskiego

Rozwiązanie jest poszukiwane jako:

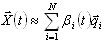(B2)

gdzie q_i są wektorami bazy rozmiaru Neq — liczba równań modelu źródła ES.

Te wektory powinny spełniać następujące wymagania:

kinematyczne i statyczne warunki obwiedni;
niezależność liniową
kompletność bazy.

Nie jest możliwe nadawanie ani wektorów Lanczosa ani żadnych wektorów uzyskanych dla jednostkowych skupionych sił węzłowych (metoda redukcji bazy dla bezpośredniego solwera lub metoda Ritz-gradient PCG_Ritz).

Rzutowanie podprzestrzenne jest definiowane jako:

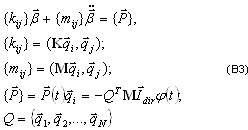
Należy zwrócić uwagę, że β jest rozmiaru N; macierz Q jest rozmiaru NeqxN.

Równanie podprzestrzenne (B3) będzie rozwiązywane przez rozłożenie wektorów własnych(na podprzestrzeni, która jest definiowana przez Q = {q1, q2,..., qN}).

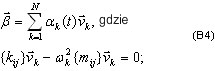
Należy zauważyć, że (4) jest dokładnym wyrażeniem, ponieważ indeks k przyjmuje wartości z zakresu od 1 do N — w całym rozmiarze podprzestrzeni Q.

Zastępowanie (B4), przez (B3) prowadzi do niezwiązanego zestawu równań

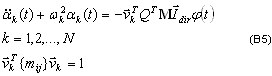
Należy rozważyć

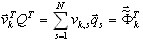(B6)

Dlatego (B5) może być wyświetlone jako

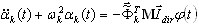(B7)

gdzie k=1,2,..., N.

Należy zastosować metodę spektrów odpowiedzi do równań niezwiązanych (B7)

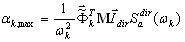(B8)

gdzie 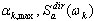to maksymalne odpowiedzi dla trybu podprzestrzeni k i funkcji przyśpieszenia spektrum, odpowiednio.

Można zastąpić (B8) przez (B4), a następnie przez (B2):

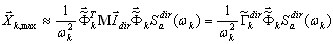(B9)

Powinno zostać zanotowane, że dla N — > Neq:

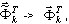
ω_k — > Ω k

gdzie Ωk, 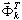są dokładną parą własną źródła ES problemu własnego

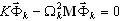(B10)

i 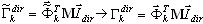, w którym 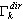jest współczynnik udziału masy dla trybu własnego k.

Konkluzje

Proponowane podejście nie wymaga „dobrego” przybliżenia 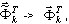, ω_k - > Ω_k. Możliwe jest, że 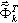, ω_k przybliża 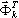, Ω_k z dowolną dokładnością.
Proponowane podejście nie jest gorsze, niż dobrze znane rozłożenie modalne (superpozycja). Obie metody te tworzą poszczególne przypadki wspólnej metody rzutowania i zbiegają się do "dokładnego" rozwiązania, jeśli N — > Neq. (Ta instrukcja nie odnosi się bezpośrednio do metody spektrów odpowiedzi , ponieważ ta metoda ma charakter statystyczny i jej zbieżność z dokładnym rozwiązaniem ma miejsce, gdy N - > ∞. Oczywiście, dla N > Neq będzie się pojawić obliczeniowy konflikt ze względu na fakt, że liczba poszczególnych wektorów nie może przekroczyć Neq. Dlatego możliwe jest uzyskanie różnych rozwiązań dla różnych wektorów bazy, gdy N = Neq. Jest to specyfika metody spektrów odpowiedzi . Dla metod innych niż metoda spektrów odpowiedzi pełna zbieżność następuje, gdy N = Neq. Zbieżność dla przypadku metody spektrów odpowiedzi powinna być uwzględniana w znaczeniu statystycznym, ponieważ metoda ta stanowi statystyczne podejście, które ma na celu uzyskanie przeciętnego rozwiązania, gdy została utracona analiza czasowa. W związku z tym termin "dokładne rozwiązanie" powinien być stosowany ostrożnie).
Która baza jest lepsza: wektory Ritza czy wektory własne? Powinna istnień taka baza, która zapewni lepszą zbieżność „dokładnemu” rozwiązaniu (N = Neq) za pomocą najmniejszej liczby funkcji bazy N. Pytanie powinno być rozwiązane przez sprawdzenie praktycznych przykładów.
Zazwyczaj pierwsza część pary 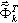, ω_k zapewnia dobre przybliżenie do odpowiedniej pary własnej 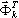, Ω_k (możliwe jest określenie dokładności dla każdej pary w kolumnie „Dokładność” listy wyjściowej). Tylko ostatnia część pary 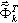, ω_k zapewnia niewłaściwe przybliżenie do wymaganych par własnych i może być traktowane jako „tryby pseudo” (z punktu widzenia francuskiej normy sejsmicznej PS-92).
Korzystanie z całej podprzestrzeni Q = {q1, q2,..., qN} zapewnia szybkie zwiększenie procentu masy. W przypadku trybów modalnych i sejsmicznych, tylko część tej podprzestrzeni jest używana.

Załącznik 3C

Poniżej podano przykłady aplikacji trybu sejsmicznego i trybu pseudo.

Oczywiście, istnieje wiele rodzajów problemów sejsmicznych i spektralnych, w których trudno jest uzyskać wystarczający (70%-90%) procent masy. Możliwe jest, aby rozwiązać problemy z rozwiązaniem tak zwanych dobrych problemów przy pomocy dobrze znanych metod.

Należy przypisać dowolną liczbę trybów N.
Obliczyć pierwsze sekwencyjne tryby N za pomocą trybu modalnego.

Jednak w przypadku trudnych problemów to podejście może okazać się nieosiągalnym. Należy wziąć pod uwagę, na przykład problemy Coreal lub Museum. Są one modelami FEM, które zostały przygotowane przez francuskich inżynierów. Procent masy dla różnej liczby zdefiniowanych trybów własnych jest wyświetlony. Tryb modalny (metoda Lanczosa) jest używany.

Historia zbieżności dla problemu Coreal

Liczba postaci zbieżnych	Masa %
44	< 1%
62	12%
75	38%
89	60%
116	74%
154	77%
179	80%

Historia zbieżności dla problemu Museum

Liczba postaci zbieżnych	Masa %
41	20%
106	40%
119	42%

Na przykład, 80% oznacza, że w przypadku dwóch kierunków sumy mas nie są mniejsze niż dana liczba Tryb modalny generuje tryby własne, podczas gdy, albo przyjęta wartość procentowa masy jest uzyskiwana lub przypisane górne ograniczenie liczby trybów jest wyczerpane. Ostateczne rozwiązanie metody spektrów odpowiedzi jest uzyskiwane w formie statystycznej superpozycji wektorów własnych.

W obu rozważanych problemach, liczba stopni swobody jest mniejsza niż 2000. Takie problemy są traktowane jako małe (z uwzględnieniem liczby stopni swobody). W przypadku dużych (ciężkich) i średnich problemów, możliwe jest, że oba modalne i sejsmiczne tryby pozostają niemożliwe do zastosowania w praktyce z powodu ekspansywnego charakteru procesu obliczeniowego. W takich przypadkach zalecane jest stosowanie trybu pseudo. Poniżej zaprezentowano historia zbieżności dla problemów Coreal i Museum.

Historia zbieżności dla problemu „Coreal”

Liczba wektorów bazy	Masa %
10	58%
20	67%
40	70%
80	80%

Historia zbieżności dla problemu „Museum”

Liczba wektorów bazy	Masa %
10	60%
20	66%
40	71%

Uwaga: Konieczne jest zdefiniowanie około 130 -150 wektorów Lanczosa, aby uzyskać 80 wektorów własnych dla trybu modalnego. Wysiłek obliczeniowy w pseudo modzie jest znacząco mniejszy (około 3-5 razy).

Zbieżność wyników w trybie pseudo jest przedstawiona w następnym problemie. Poniższa tabela przedstawia wynikłe wartości max/min kombinacji CQC dla trybu modalnego i trybu pseudo.

Postać	UX (cm)	UY (cm)	UZ (cm)	Procent masy.
Modalna	5.52002e-00	5. 88293e—00	5.83013e—00	81%
Pseudo, Nvect = 10	5.58710e—00	5. 89055e—00	5.00224e-00	80%
Pseudo, Nvect = 20	5.52937e—00	5.88870e—00	6.08661e—00	91%

Nvect — liczba wektorów bazy.

Załącznik 3D

Aplikacja metody analizy modalnej do rozwiązania dużej skali problemów

Przykład 1

Porównanie czasu obliczeń dla BLSI i metody Lanczosa. Różne liczby trybów własnych są brane pod uwagę.

Zastosowany solwer: bezpośredni solwer sparse. Typ macierzy masy: skupiona z rotacjami.

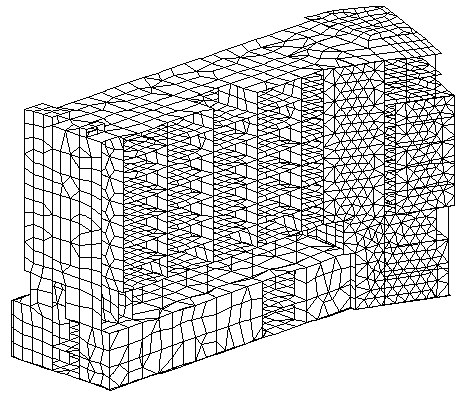
Rys. D1. Model hotelu. Liczba węzłów: 6 359; liczba elementów: 7 264; liczba równań: 37 806.

Tabela D1. Porównanie wyników

BLSI		Lanczos
f (Hz)	Dokładność	F (Hz)	Dokładność
2,794e—001	1,082e-006	2,794e-001	5,680e—015
1,388e + 000	1,389e—004	1,388e + 000	2,199e-013
1,520e + 000	7,847e-004	1,520e + 000	8,193e—012
1,644e + 000	2,469e—004	1,644e + 000	4,497e—013
1,747e + 000	2,691e—004	1,747e + 000	5,455e—014
1,776e + 000	3,092e—004	1,776e + 000	9,127e—013
1,806e + 000	3,153e—004	1,806e + 000	6,621e—013
1,818e + 000	6,383e—004	1,818e + 000	3,656e—012
2,622e+000	1,565e-003	2,343e+000	2,047e—011
2,634e+000	1,383e—003	2,622e+000	1,223e—005

Ponieważ sprawdzenie Sturma nie jest wykonywane, pominięte pary własne występują między 8^—ym i 9^—ym trybem, gdy BLSI jest zastosowany.

Tabela D2. Trwanie wyodrębniania trybu (w sekundach)

Metoda	10 trybów	50 trybów	100 trybów
BLSI	735	6029	23572
Lanczos	1472	12637	25271

Faktoryzacja macierzy: 841 s.

Zaawansowane metody (BLSI, Lanczos) na podstawie potężnego bezpośredniego solwera sparse pozwalają na szybkie tworzenie faktoryzacji macierzy i wyodrębnienie dużej liczbę trybów własnych. Obliczenia były wykonywane na komputerze P—350 (256 MB pamięci RAM).

Przykład 2

Zastosowanie różnych metod do rozwiązania problemu PJG203. Model zawiera połączenia sztywne, co prowadzi do użycia rozłożonej macierzy mas. 25 trybów pseudo zostało wyodrębnionych.

Rys. D2. Problem PJG203. Liczba węzłów: 5 945; liczba elementów: 11 471; liczba połączeń sztywnych: 22; liczba zgodnych węzłów: 302; liczba równań: 34 266.

Tabela D3. Czas obliczeń, pojemność dysku, pierwsze dziesięć częstotliwości i odpowiednia dokładność dla różnych metod.

Metoda	Czas (s.)	HDD (MB)	Częstotliwości (Hz)	Dokładność
Skyline	61 633	597	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.829e+000 3.033e+000 3.209e+000 3.595e+000	8.043e—015 1.025e—013 1.031e—013 1.712e—006 5.566e—006 6.331e—008 3.538e—001 3.052e—005 9.086e—005 4.498e—003
Sparse	4 435	99	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.825e+000 3.033e+000 3.209e+000 3.595e+000	3.522e—012 2.689e—011 1.159e—010 1.735e—006 5.639e—006 6.419e—008 3.520e—001 3.034e—005 9.938e—005 4.386e—003
Modyf. Lanczos	3 459	24	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.791e+000 3.033e+000 3.209e+000 3.595e+000	3.719e—004 3.891e—004 6.601e—004 1.454e—003 1.875e—003 2.946e—003 3.364e—003 3.923e—003 2.175e—002 1.580e—001
PCG_Ritz	1 521	24	1.266e+000 1.350e+000 1.467e+000 2.445e+000 2.446e+000 2.446e+000 2.805e+000 3.035e+000 3.381e+000 3.566e+000	N/A — PCG_Ritz nie jest interaktywną metodą, jest to metoda Ritza. W związku z tym pseudo mody są uzyskiwane zamiast "dokładnych" trybów własnych

Następujące parametry zostały użyte do modyfikacji metody Lanczosa: solwer iteracyjny AEBEIS (tryb wielopoziomowy); uwarunkowania wstępne ICCF; 2 poziomy agregacyjne; 4 wewnętrzne iteracje, tol = 1.0e-04 — dokładność generowania wektorów Lanczosa.

Następujące parametry została przyjęta dla metody PCG_Ritz: wielopoziomowy iteracyjny solwer AEBEIS; uwarunkowanie wstępne ICCF ; 1 poziom agregacyjny; 4 wewnętrzne iteracje

Zbieżne częstotliwości są oznaczone na czerwono. Jeśli dokładność (zobacz załącznik 3A) względnych norm wektora residualnego dla danego trybu jest mniejsza niż 5.0e-02, taka norma może być traktowana jako w pełni zbieżna z odpowiednim wektorem własnym. W związku z tym częstotliwości oznaczone na czerwono są traktowane jako dokładna wartość dla danego modelu dyskretnego. Szacunek błędów dla metody PCG_Ritz jest prezentowany w tabeli D4. Może być podsumowane, że wyniki uzyskiwane za pomocą metody PCG_Ritz zapewniają dostatecznie dobre przybliżenie dla celów inżynieryjnych i takiej podejście może być używane do szybszego oszacowania zachowań sejsmicznych.

Metody zaawansowane pozwalają, aby znacząco zredukować czas obliczeń i wymagania względem pojemności dysku bez poważnej utraty poprawność.

Tabela D4. Szacunek błędów dla metody PCG_Ritz

"dokładna" częstotliwość	wyniki PCG_Ritz	Błąd (%)
1.175e+000	1.266e+000	7.7
1.337e+000	1.350e+000	1.0
1.454e+000	1.467e+000	0.9
2.445e+000	2.445e+000	0.0
2.445e+000	2.446e+000	0.0
2.628e+000	2.446e+000	7.0
2.791e+000	2.805e+000	0.5
3.033e+000	3.035e+000	0.1
3.209e+000	3.381e+000	5.4
3.595e+000	3.566e+000	0.8

Obliczenia są wykonywane w komputerze PC—450 (128 MB pamięci RAM).

Przykład 3

Uwzględniana jest cienka płyta kwadratowa z rozłożoną macierzą mas zamykaną wzdłuż jednej krawędzi. Element skorupy czterowęzłowej i siatka 128x128 (liczba równań Neq wynosi 99072) są używane. 40 trybów pseudo jest wyodrębnianych.

Czas obliczania i ilość miejsca na dysku dla przechowywania metody Lanczosa (skyline i sparse), zmodyfikowanej metody Lanczosa (solwer iteracyjny) i metody Ritz-gradient (PCG_Ritz) są przedstawione w tabeli D5.

Tabela D5. Wymagania co do czasu obliczania i pojemności dysku dla kilku metod.

Metoda	Czas (s.)	HDD (MB)
Lanczos, solwer skyline	141 559	7 367
Lanczos, solwer sparse	15 615	157
Zmodyfikowany Lanczos, solwer iteracyjny	18 978	0 — w rdzeniu
PSG_Ritz	9 651	192

Obliczenia są wykonywane w komputerze PC—450 (128 MB pamięci RAM).

pierwsze dziesięć częstotliwości uzyskanych przez Lanczosa (skyline lub sparse) i modyfikowanego Lanczosa (solwer iteracyjny, uwarunkowania wstępne ICCF, 3 poziomy agregacyjne, 8 wewnętrznych iteracji, tolerancja 1.0e—03 dla generowania wektorów Lanczosa zostały przyjęte) są identyczne. W związku z tym, że dokładność obliczeń jest bardzo duża, było możliwe, aby rozważyć takie wartości, które znajdują się dokładnie w danym modelu dyskretnym. Są one przyjęte jako wartości etalon dla szacunku błędów dla częstotliwości uzyskanej przez metodę PCG_Ritz. To podejście wielopoziomowe z uwarunkowaniami wstępnymi ICCF (jeden poziom agregacyjny, 4 wewnętrzne iteracje) zostało wybrane podczas stosowania metody PCG_Ritz. Odpowiednie wyniki są prezentowane w tabeli D6.

Tabela D6. Porównanie częstotliwości dla metod PCG_Ritz i Lanczosa

Częstotliwości według Lanczosa (Hz)	Dokładność	Częstotliwości według PCG_Ritz (Hz)	Błąd (%)
3.722e+000	5.918e-014	3.725e+000	0.08
9.112e+000	4.474e—014	9.115e+000	0.03
2.282e+001	2.424e—012	2.284e+001	0.09
2.915e+001	5.866e—013	2.915e+001	0.00
3.315e+001	1.795e—013	3.318e+001	0.09
5.801e+001	2.373e—011	5.803e+001	0.03
6.565e+001	3.028e—011	6.571e+001	0.09
6.873e+001	6.907e—014	6.875e+001	0.03
7.602e+001	1.549e—012	7.609e+001	0.09
9.949e+001	3.302e—013	9.953e+001	0.04

Przykład 4

Duży budynek jest prezentowany na rys. D3

Rys. D3 Duży budynek. Liczba węzłów: 26126, liczba elementów: 30272,

liczba równań: 155920.

Liniowa analiza statyczna (pojedynczy przypadek obciążenia) i wyodrębnianie 10 trybów własnych są brane pod uwagę. Tolerancja przyjęta dla powtarzającego się rozwiązania jest równa 1.0e—04. Dla solwera skyline metoda Lanczosa jest używana. Dla solwerów bezpośrednich sparse stosowane są zarówno metoda Lanczosa jak i BLSI. Zmodyfikowana metoda Lanczosa jest używana dla solwera iteracyjnego (metoda wielopoziomowa z 3 poziomami agregacyjnymi, 4 wewnętrzne iteracje, warunki wstępne ICCF). Przyjmuje się macierz mas typu: skupiona z rotacjami

Tabela D7. Czas obliczania i miejsce na dysku dla kilku metod

Metoda	Miejsce na dysku (MB)	Statystyka liniowa (single rhs) (s)	Wyodrębnianie 10 trybów własnych (S)	Całkowity czas (s)
Skyline	5 702	136 065	65 052	203 878
AEBEIS	52	2 442	25 793	28 355
Sparse (metoda Lanczosa)	773	10 253	24 500	35 762
Sparse NS (metoda BLSI)	773	10 253	11 534	22 604

Obliczenia są wykonywane w komputerze PC—450 (128 MB pamięci RAM).

Konkluzje

Zaawansowane metody: BLSI, Lanczosa na podstawie bezpośredniego solwera sparse i wysoce wydajnego solwera iteracyjnego AEBEIS z uwarunkowaniami wstępnymi ICCF to skuteczne narzędzia do rozwiązywania dużych liniowych statyk i problemów wartości własnej. Skracają one znacznie czas obliczeń i wymagania względem pojemności dysku w porównaniu do konwencjonalnego solwera skyline. Metoda Ritz-gradient PCG_Ritz umożliwia szybkie oszacowanie zachowania sejsmicznego danej konstrukcji. Jeśli pojedynczy poziom agregacyjny zostanie zaakceptowany, odpowiednie wyniki, uzyskanego przez metodę PCG_Ritz są podobne do tych, które zostały uzyskane przez metody Lanczosa lub BLSI.

Materiały referencyjne

E.L.Wilson. An eigensolution strategy for large systems. ComputersStructures, Vol.16, No. 1-4 ss.259—265, 1983.
Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21—23, North—Holland.
E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, California, USA, 1996.
R.W.Clough, J.Penzien. Dynamics of Structures. McGraw—Hill Book Comp., 1975, s. 634.
Fialko S. Yu. Investigations of the Initial Imperfections Influence to Natural Vibrations of Ribbed Conical Shells, Soviet Applied Mechanics, 1982, 18, N11, ss.118 — 122. (w języku rosyjskim)
Fialko s. Yu. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, v23, N6, ss. 547—552.
Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. ss.193—207.
Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics — engineering sciences), IV, 2000
Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 — 60, 1988.
Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 — 69, 1989.
Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 — 207, 1987.
M.Papadrakakis, Solving large—scale problems in mechanics, John Wiley & Sons Ltd., 1993.
S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, ss.75—104.
Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26—27, 1987.
Hughes T.J.R., R.M.Ferencz, i j.O.Hallquist. Large—scale vectorized implicit calculations in solid mechanics on a CRAY X—MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
Hughes Th. J. R. "The Finite Element Method. Linear Static and Dynamic. FEM Analysis."
Parlett B.N., 1980. "The Symmetric Eigenvalue Problem". Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 — 471, 1997.
Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829—840, 1994.
Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529-3544, 1995.
Regulatory Guide
I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Oscillations of Ribbed Shells of Revolution, Kiev, Naukova Dumka, 1988, ss. 169 (In Russian).
S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, v20, N11, ss. 1033—1037. (w języku angielskim)