Przedstawiona zostanie metoda wyznaczenia spektrum odpowiedzi Sa=Sa(T) dla danego wykresu przyspieszeń F(t), gdzie T jest okresem, Sa jest spektrum przyspieszenia, t oznacza czas oraz F(t) — dana funkcja analizy czasowej.
Ta opcja może być przydatna, jeżeli musimy porównać odpowiedzi sejsmiczne otrzymane zarówno przy użyciu analizy spektralnej jak i analizy czasowej. W takim przypadku należy przypisać krzywą spektrum odpowiedzi Sa=Sa(T), która dokładnie pokrywa się z daną funkcją analizy czasowej F(t) (zapis wykresu przyspieszeń).
Ta opcja pozwala na analizę dynamicznej odpowiedzi konstrukcji przy użyciu metody spektrum odpowiedzi (analiza spektralna) dla bieżącego zapisu wykresu przyspieszenia. Pseudospektralne przyspieszenie jest maksymalnym przyspieszeniem pojedynczego stopnia swobody wywołanym poprzez dany wykres przyspieszenia:
gdzie
Tp — czas trwania zapisu trzęsienia ziemi, ω = 2π/T — pulsacja dla Tmin ≤ T ≤ Tmax, ξ — parametr tłumienia (wyrażony w procentach w stosunku do tłumienia krytycznego), F(t) – dany wykres przyspieszenia.
Zakładamy, że dana jest funkcja analizy czasowej F(t) — rysunek 1. Kolejność problemów Cauchy'ego dla punktów (2) dla T = T1 < T2 <... < Tn zostanie zintegrowana numerycznie, gdzie
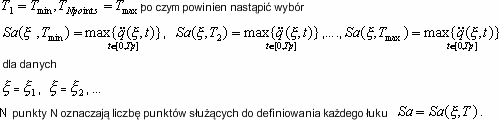
Spektrum odpowiedzi przedstawiono na rysunku 2.
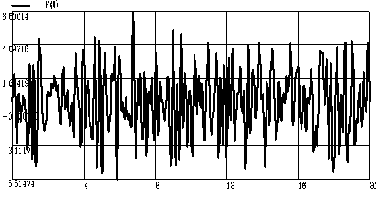
Rys. 1
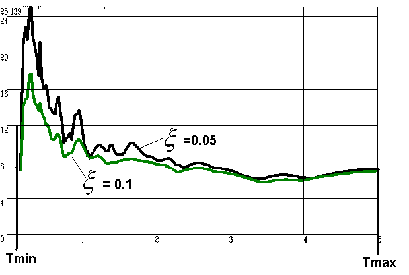
Rys. 2