Uma spline é uma curva suave que passa através de ou perto de um conjunto de pontos que afetam a forma da curva.
Por padrão, uma spline é uma série de segmentos de curva mesclados de polinômios de grau 3 (também denominados polinômios cúbicos). As curvas são tecnicamente denominados B-splines não uniformes e racionais (NURBS), mas são designadas como splines para simplificar. As splines cúbicas são as mais comuns; elas imitam as splines criadas manualmente por meio de tiras flexíveis cuja forma é obtida colocando-se pesos em pontos de dados.
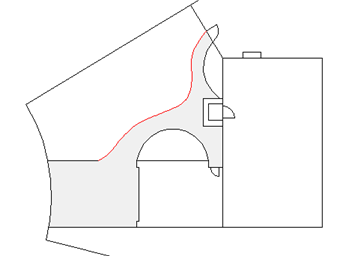
No exemplo a seguir, foi usada uma spline para criar o limite ressaltado da calçada de concreto.
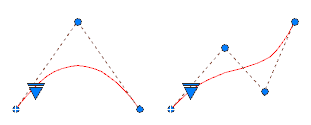
Compreender os vértices de controle e os pontos de ajuste
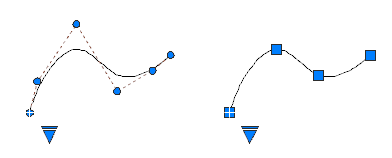
É possível criar ou editar splines usando vértices de controleou pontos de ajuste. A spline da esquerda exibe vértices de controle ao longo de um polígono de controle e a spline da direita exibe pontos de ajuste.
Utilize a alça triangular em uma spline selecionada para alternar entre exibir vértices de controle e exibir pontos de ajuste. Você pode usar as alças redondas e quadradas para modificar uma spline selecionada.
Criar splines usando vértices de controle
Quando você cria splines usando vértices de controle, os pontos que você especifica exibem linhas temporárias entre eles, formando um polígono de controle que determina a forma da spline.
A vantagem de alterar a forma de uma spline utilizando-se vértices de controle é alta precisão que esse método fornece. Com esse método, você também pode especificar polinômios de grau inferior ou superior, incluindo grau 1 (linear), grau 2 (quadrático), grau 3 (cúbico) e assim por diante até o grau 10.
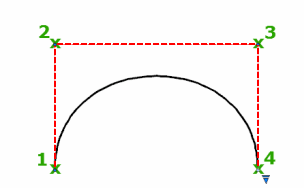
Criar splines usando pontos de ajuste
Quando você cria splines utilizando pontos de ajuste, a curva resultante passa através dos pontos especificados e é influenciada pelo espaçamento dos nósmatemáticos na curva.
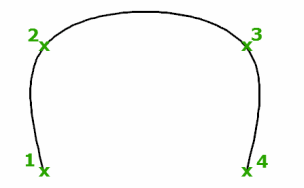
Você pode escolher o espaçamento desses nós com a opção parametrização de nós, que resultará em curvas diferentes, como mostrado no exemplo.
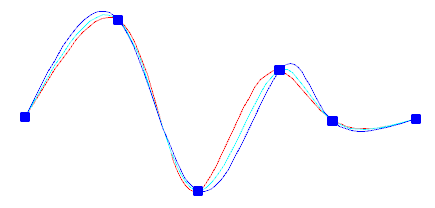
Quando o valor de tolerância é definido como 0, a spline passa diretamente através dos pontos de ajuste. Com valores de tolerância maiores, a spline passa perto dos pontos de ajuste. Como opção, você pode especificar a direção da tangente à spline em cada extremidade.
Casos especiais
Você pode criar uma spline com uma forma parabólica especificando uma spline de grau 2 criada com exatamente 3 vértices de controle, como mostrado à esquerda. As splines de grau 3 criadas com 4 vértices de controle têm a mesma forma das curvas de Bézier de grau 3, como mostrado à direita.