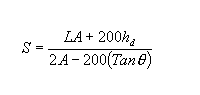O Autodesk Civil 3D pode calcular valores da definição geométrica de uma curva vertical, informações PVI, assim como de objeto e de altura do olho.
Estes valores são derivados a partir de equações empíricas e não utilizam a velocidade do projeto.
Para uma curva vertical convexa, as distâncias de visibilidade de parada e passagem são utilizadas porque uma curva de pico pode obstruir uma visibilidade do controlador da superfície da rodovia ou outro objeto.
Distância de visibilidade de parada e de passagem não são usadas para uma curva vertical côncava porque não há nenhum pico de curva para obstruir a visibilidade do controlador da pista de superfície ou outro objeto. Durante o dia, com melhor visibilidade, o controlador apresenta uma vista completa da estrada em uma curva vertical côncava. Durante a noite, no entanto, o controlador pode ver somente até a distância da viga do farol. Para projetar uma curva vertical côncava, é possível utilizar a distância de visibilidade do farol.
Você pode exibir estas propriedades no Autodesk Civil 3D 2024 utilizando o Editor de texto do componente. No Toolspace, na guia Configurações, expanda Perfil 
Estilos de legenda Curva. Clique duas vezes no estilo de legenda cume padrão e côncavo. Clique na guia Layout. No Nome do componente, selecione um item como BVC. No Editor de texto do componente, clique na seta da lista suspensa em Propriedades para exibir a lista de propriedades disponíveis. Navegue para baixo para ver as propriedades como a distância de visibilidade da luz frontal, a distância de visibilidade de ultrapassagem, e assim por diante.
Criar curvas verticais convexas com base nas distâncias de visibilidade de parada e de passagem
A distância de visibilidade de ultrapassagem é a distância necessária para um controlador ver um veículo em movimento e determinar se há distância suficiente para permitir uma pista de ultrapassagem. A distância de visibilidade de ultrapassagem não é usada no projeto de curva vertical convexa frequentemente porque o comprimento da curva necessário para atender os critérios de visibilidade de passagem são normalmente proibitivos.
Distância de visibilidade de parada, um critério amplamente utilizado para determinar o comprimento da curva, é a distância necessária para um controlador para ver um risco na superfície da rodovia. Diretrizes governamentais para determinar a distância de visibilidade de requisitos de ultrapassagem e passagem.
As seguintes equações calculam os comprimentos da curva vertical convexa usando as distâncias de visibilidade de parada e de passagem.
onde:
L = Comprimento da curva vertical em pés (ou metros)
S = Distância de visibilidade em pés (ou metros)
A = Diferença algébrica na porcentagem de declividade (%)
h1 = Altura do olho do observador acima da superfície da rodovia em pés (ou metros)
H2 = Altura do objeto acima da superfície da rodovia em pés (ou metros)
A seguinte equação soluciona para L quando S for menor que L:
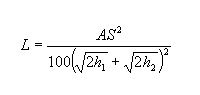
A seguinte equação soluciona para S quando S for menor que L:
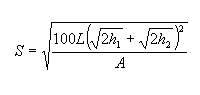
A seguinte equação soluciona para L quando S for maior que ou igual a L:
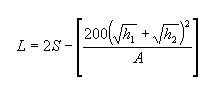
A seguinte equação soluciona para S quando S for maior que ou igual a L:
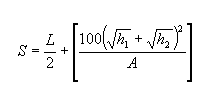
Criando curvas verticais côncavas com base na distância de visibilidade de farol
Durante a noite, as vigas de farol de um veículo definem a distância de visibilidade. Uma curva vertical côncava intercepta uma viga de farol na superfície da rodovia e limita o comprimento da viga. A distância de visibilidade da luz do farol mede o topo da viga do farol acima do pavimento e o ângulo máximo do farol para determinar o comprimento da curva. A altura do olho do controlador também é incluída.
As seguintes equações de distância de visibilidade do farol são utilizadas para criar curvas verticais côncavas.
onde:
A = Diferença algébrica na porcentagem de declividade (%)
hd = altura da viga do farol acima do pavimento em pés (ou metros)
L = Comprimento da curva vertical em pés (ou metros)
S = Distância de visibilidade em pés (ou metros)
Ø = ângulo da curva ascendente da viga do farol da horizontal (normalmente 1 grau)
A seguinte equação soluciona para L quando S for menor que L:
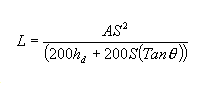
A seguinte equação soluciona para S quando S for menor que L:
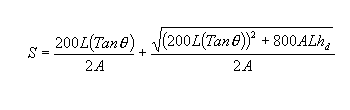
A seguinte equação soluciona para L quando S for maior que ou igual a L:
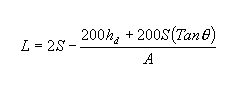
A seguinte equação soluciona para S quando S for maior que ou igual a L:
