O comprimento de passagem da correia é determinado pelo número de dentes da correia e pela folga circular. A trajetória da correia é baseada na posição da polia individual. O diâmetro do flanco de cada polia é determinado pelas seguintes equações. A posição da polia deslizante é ajustada para cumprir os critérios regulares de comprimento de correia. O cálculo utiliza a solução de iteração para localizar a posição adequada da polia deslizante que mais se aproxima da posição desejada.
Cálculo do diâmetro do flanco exato
|
|
Polia síncrona no sentido dos ponteiros do relógio ou correia de dupla face |
|
|
|
|
|
Polia plana no sentido dos ponteiros do relógio ou correia de dupla face |
|
D p = D + 2(a + h t ) |
|
|
|
Polia síncrona no sentido contrário aos ponteiros do relógio e correia de face única |
|
D p = D 0 + 2(H - a - h t ) |
|
|
|
Polia plana no sentido contrário aos ponteiros do relógio e correia de face única |
|
D p = D + 2(H - a - h t ) |
Exemplo de transmissão de potência com 2 polias
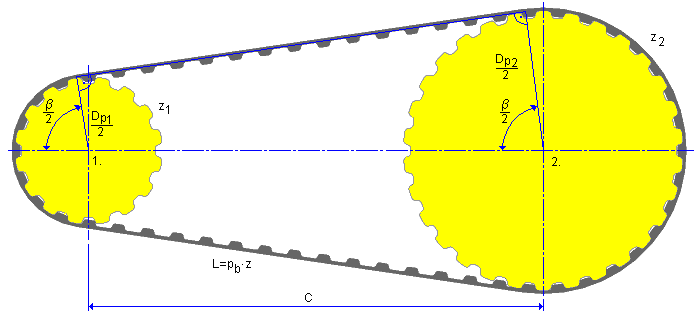
Arco de contato
![]()
Comprimento da correia de folga
![]()
Distância ao centro
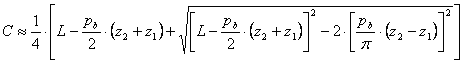
Recomenda-se utilizar a fórmula a seguir para calcular a distância ao centro de uma nova transmissão
0.2 p b (z 1 + z 2 ) ≤ C ≤ 0.7 p b (z 1 = z 2 )
Significado das variáveis utilizadas:
|
z |
Número de dentes da polia especificada/Número de dentes da correia [-] |
|
p b |
Folga circular [m] |
|
D |
Diâmetro nominal da polia plana [m] |
|
a |
Deslocamento da linha de passo [m] |
|
h t |
Altura do dente da correia [m] |
|
D 0 |
Diâmetro externo da polia síncrona [m] |
|
H |
Altura da correia [m] |
|
C |
Distância ao centro da polia especificada e da polia de transmissão [m] |
| β |
Arco de contato [gr] |