脱层演变定律(或损坏演变定律)
必须进行定义的粘性本构关系的最后一部分是标量损坏变量 D 的演变表达式。
损坏演变模型必须能够准确地表示损坏变量 D 从初始值 0 到最终值 1 的演变,不管是否准确地记录了粘性材料承受的组合载荷。请注意,可以开发依据应变(例如,相对位移)或应力表示的损坏演变模型,如果没有初始实现,我们将采取基于应变(相对位移)的方法。可以假设损坏演变会受到法线和剪切相对位移不同程度的影响,因为这种假设有合理性又直观。但是,为了简单起见,我们假设损坏演变可以表示为单独标量测量相对位移的函数(称为有效相对位移 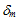 ),其中
),其中
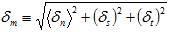
相应的有效面力将定义为 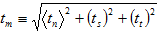
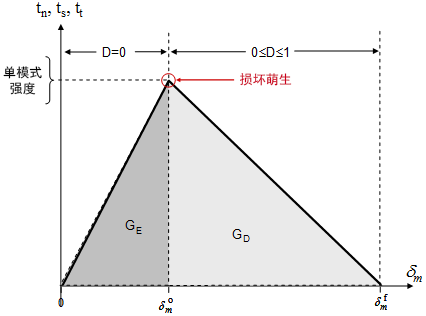
在上图中,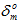 表示损坏萌生时有效相对位移
表示损坏萌生时有效相对位移 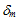 的值,例如在
的值,例如在
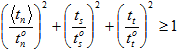
感到满意时。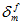 表示材料刚度完全降到零时有效相对位移
表示材料刚度完全降到零时有效相对位移 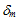 的值。
的值。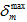 表示到目前为止(即 t 小于或等于当前时间的任何时间)材料已获得的有效相对位移
表示到目前为止(即 t 小于或等于当前时间的任何时间)材料已获得的有效相对位移 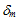 的最大值。请注意,
的最大值。请注意,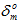 和
和 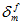 被视为材料特征化的一部分。
被视为材料特征化的一部分。
对于 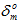
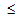
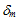
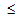
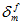 范围内
范围内 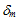 的任何值,损坏变量 D 的当前值可以通过以下损坏演变方程表示。
的任何值,损坏变量 D 的当前值可以通过以下损坏演变方程表示。
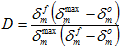
应当强调的是,Helius PFA 中提供的这三种粘性本构模型之间的主要差异在于为了评估损坏演变而计算 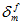 的精确方式。对于总位移模型,只需将损坏萌生
的精确方式。对于总位移模型,只需将损坏萌生 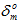 时的有效相对位移添加到用户指定的参数 (
时的有效相对位移添加到用户指定的参数 (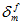 -
- 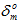 ),即可计算出
),即可计算出 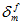 的值。因此,在发生损坏萌生并获知
的值。因此,在发生损坏萌生并获知 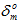 后,材料完全降级时 (
后,材料完全降级时 (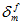 ) 的有效相对位移将保持固定不变,即使粘性材料的组合载荷状态发生更改。
) 的有效相对位移将保持固定不变,即使粘性材料的组合载荷状态发生更改。
要了解如何计算总能量模型或混合模式幂律的 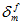 ,我们必须先定义一些能量的表达式。在任意时间点,与法线和剪切变形相关联的各个能量组件被定义为
,我们必须先定义一些能量的表达式。在任意时间点,与法线和剪切变形相关联的各个能量组件被定义为
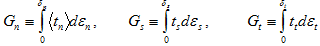
粘性材料吸收的总能量只是这三种能量组件之和。
Gtotal = Gn + Gs + Gt
当总能量 Gtotal 达到临界总能量值 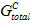 时,则表示粘性材料已完全降到零刚度,并且再也无法支持任何载荷。因此,知道临界总能量值
时,则表示粘性材料已完全降到零刚度,并且再也无法支持任何载荷。因此,知道临界总能量值 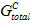 ,可以计算出在粘性材料达到完全降级时的有效相对位移
,可以计算出在粘性材料达到完全降级时的有效相对位移 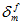 ,如下所示。
,如下所示。
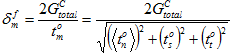
对于总能量模型,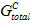 永远不会发生变化。无论面力的瞬时混合是否应用到粘性材料,此用户指定的常数均相同。对于混合模式幂律,
永远不会发生变化。无论面力的瞬时混合是否应用到粘性材料,此用户指定的常数均相同。对于混合模式幂律,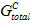 的值会不断发生更改以响应面力组件(作用于粘性材料)混合的变化。在混合模式幂律中,可以通过将 Gn、Gs 和 Gt 均匀放大到满足以下标准时来获取
的值会不断发生更改以响应面力组件(作用于粘性材料)混合的变化。在混合模式幂律中,可以通过将 Gn、Gs 和 Gt 均匀放大到满足以下标准时来获取 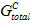 的瞬时值。
的瞬时值。
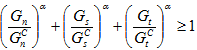
鉴于任何瞬时组的面力(tn、ts、tt)及其瞬时各个能量密度组件(Gn、Gs、Gt),我们可以使用上述标准并将这些面力均匀放大到满足该标准的级别。让我们将此缩放后的面力表示为 (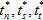 ),并将其相应缩放能量组件表示为 (
),并将其相应缩放能量组件表示为 (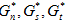 )。鉴于有了会导致脱层传播的投影能量组件 (
)。鉴于有了会导致脱层传播的投影能量组件 (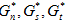 ),我们现在可以将导致脱层传播的总能量计算为
),我们现在可以将导致脱层传播的总能量计算为 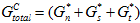 。
。