渐进式失效分析的收敛问题
解决大部分渐进式失效问题遇到的常见难题。
大多数商业有限元代码使用基于牛顿-拉弗森算法的方程求解器。牛顿-拉弗森算法的使用所隐含的基本假设是,系统的非线性响应非常平滑。如果系统的非线性响应确实非常平滑,并且牛顿-拉弗森算法使用非常接近实际求解的近似求解启动,则牛顿-拉弗森算法会产生一系列显示二次收敛的求解(定性显示在下图部分 A 中)。
但是,在渐进式失效分析中,系统的非线性响应并不平滑,特别是在材料的本构行为中,材料失效导致较大的中断的局部级别上(例如,查看单向复合材料中的损坏状态部分中的图形)。系统非平滑响应完全改变了非线性求解过程的收敛特征。下图部分 B 定性显示了在求解非平滑系统时发生的收敛行为(例如在渐进式失效分析中遇到的收敛行为)类型。在部分 B 中观察到的最重要特征是,最大残余力的大小不一定在执行平衡迭代时会显示持续降低现象。实际上,最大残余力的大小会保持相对稳定,直到残余力突然消失,而这也指示求解已找到。
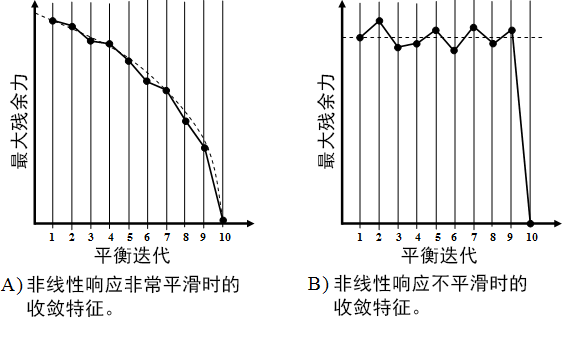
大多数商业有限元代码使用的默认非线性求解策略基于以下假设:系统将显示在上述部分 A 中描述的收敛特征。特别是商业 F.E. 代码需要最大残余力大小来显示在执行平衡迭代时持续且快速的降低现象。如果残余力没有随着每个新平衡迭代而大幅降低,则商业 F.E. 代码会假设当前时间增量中的非线性数量过多。因此,商业 F.E. 代码选择降低时间增量大小,以尝试限制系统响应中的非线性数量。此理念不适用于渐进式失效分析,因为系统的非线性响应不平滑,并且残余力不需要显示持续降低现象。实际上,将此方法用于渐进式失效分析会适得其反,会导致使用过小的时间增量,从而使完成分析无法完成。
Firehole Composites(现属于 Autodesk)已经开发了在 Helius PFA 中实现的专有算法,以解决通常与材料刚度快速降级关联的收敛难题。当 Helius PFA 用于提供材料刚度降级时,有限元代码会显示渐进式失效模拟的强大收敛。根据渐进式失效分析的大量经验,建议在评估减少载荷增量大小的需求之前,有限元代码应该允许执行至少 50 次平衡迭代。