纤维成分失效准则
以下假设在开发纤维成分失效准则时使用。
假定纤维失效受纤维平均应力分量
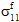 、
、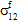 和
和 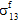 影响。
影响。假定纤维失效与纤维平均应力分量
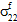 、
、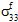 和
和 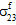 无关。
无关。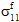 对生成纤维失效的影响取决于
对生成纤维失效的影响取决于 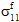 是拉伸还是压缩。
是拉伸还是压缩。假定纤维成分为横向各向同性;因此,无法区分
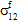 和
和 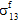 对纤维失效的影响。
对纤维失效的影响。在单向复合材料中,纤维成分视为横向各向同性材料;但是,假定纤维失效是各向同性事件。换句话说,无论负责生成纤维失效的应力分量的特定组合为何,纤维失效对纤维成分的刚度的影响保持不变。特别是,当发生纤维失效时,将每个纤维平均模量(
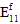 、
、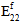 、
、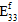 、
、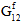 、
、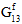 、
、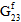 )减少为用户定义的其原始值百分比(默认值为 1%),同时假定纤维平均泊松比(
)减少为用户定义的其原始值百分比(默认值为 1%),同时假定纤维平均泊松比(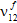 、
、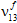 、
、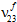 )保持不变。注意:此刚度降低方案暗示,无论导致纤维失效的应力分量的组合为何,只存在一个纤维失效模式,它导致所有纤维模量的均匀降级。
)保持不变。注意:此刚度降低方案暗示,无论导致纤维失效的应力分量的组合为何,只存在一个纤维失效模式,它导致所有纤维模量的均匀降级。在织物复合材料中,假定纤维失效是正交各向异性事件;特别是
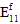 、
、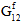 和
和 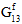 降级,而
降级,而 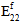 、
、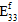 和
和 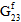 保持不变。
保持不变。
使用这五个基本假设,怀俄明大学和 Autodesk 的研究已开发出以下纤维失效准则,该准则以纤维平均应力分量的二次函数的形式表示。

量  (i = 1,4) 是纤维平均应力状态的两个横向各向异性变量。
(i = 1,4) 是纤维平均应力状态的两个横向各向异性变量。

量 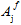 (j = 1,4) 是纤维失效准则的可调整系数。在方程26 中,如果上标符号“±”在系数
(j = 1,4) 是纤维失效准则的可调整系数。在方程26 中,如果上标符号“±”在系数 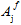 前,则它指示该值取决于关联的纤维平均应力是拉伸还是压缩;因此
前,则它指示该值取决于关联的纤维平均应力是拉伸还是压缩;因此  表示两个可能的值。因此,纤维失效准则(方程26)包含三个可调整系数,这些系数必须使用测量的复合材料强度来确定。
表示两个可能的值。因此,纤维失效准则(方程26)包含三个可调整系数,这些系数必须使用测量的复合材料强度来确定。
值得注意的是,组成不变量的纤维平均应力分量是总应力项。也就是说,它们同时包含机械应力和热应力。当激活热残余应力计算时,材料的固化后冷却所引发的纤维成分中的残余应力明确包含在总应力中(在任何外部应用的机械或热载荷之前)。这些残余应力是由于纤维和基体成分的热膨胀系数中的差异所造成的。通常,在复合材料的固化后冷却期间,基体成分将尝试收缩得比纤维成分的更多。因此,基体成分将显示拉伸热残余应力,纤维成分将显示压缩残余应力。有关如何确定这些热残余应力的说明,请参见热残余应力主题。
总体上,基体和纤维成分失效准则包含总共 13 个用于单向复合材料的可调整系数和 6 个用于织物复合材料的可调整系数。稍后介绍确定这些系数值的步骤(单向复合材料的失效准则)。