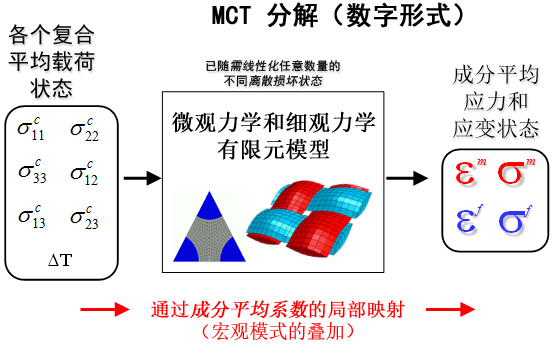
MCT 分解的数字形式

根据复合材料的有限元模型的使用，查看数字分解。

复合材料通常比仅包含纤维和基体成分的简单的单向纤维增强材料更复杂。例如，织物和编织复合材料包含由两个或多个牵引和纯基体支座系列（即，中位成分）组成的微结构。牵引中位成分由微观成分（纤维和基体）组成。在这种情况下，织物复合平均应力和应变状态必须分解为适当的中位成分平均应力和应变状态。然后，中位成分平均应力和应变状态必须进一步分解为微观成分（纤维和基体）平均应力和应变状态。Helius PFA 使用早期描述的分析二进制分解（MCT 分解的分析形式）执行最终分解。但是，分析二进制分解对于执行第一个分解（从复合平均值到中位成分值）并不切合实际，因为有两个以上的中位成分。对于包含两个以上的微观成分的复合材料，分析二进制分解也是不切合实际的。对于三个或更多中位成分或微观成分的分解，Helius PFA 基于复合材料中位成分或微观成分的有限元模型的使用来使用数字分解。

下图显示了数字分解方法的原理图，该方法依赖于复合材料的中位结构和微观结构的高保真度有限元模型。例如，对于平织复合材料，数字方法需要使用织物复合材料（该材料已使用扭曲牵引、填充牵引和基体支座的经过均质处理的材料描述）的中尺度有限元模型，即具有三个中位成分的有限元模型。各均质宏观应力状态可在中尺度有限元模型上实施，而且生成的求解可用于计算经过均质处理的扭曲牵引、经过均质处理的填充牵引和纯基体支座中的平均应力和应变状态。这些中尺度有限元求解可用于计算影响系数集，其直接将宏观应力和应变成分映射到扭曲牵引、填充牵引和基体支座的中位成分平均应力和应变状态中。这些中位成分影响系数集由织物复合材料所展示的每个离散损坏状态确定。生成的系数存储在材料数据库中，以便于在结构级渐进式失效分析模拟期间即时访问。最后，可以使用分析二进制分解将经过均质处理的扭曲牵引和填充牵引中的平均应力和应变状态分解为纤维和基体平均应力和应变状态。