Tuto část použijte k zobrazení příkladů formátů XML, které lze použít pro různé způsoby výpočtu klopení.
Příklad standardního způsobu výpočtu
Následující příklad ukazuje formát XML, který můžete použít k výpočtu staničení přechodu pro nerozdělené vozovky se základním střechovitým příčným sklonem pomocí standardní metodiky AASHTO:
<SuperelevationAttainmentMethod name="AASHTO 2001 - Crowned Roadway">
<AttainmentStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula ="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="LCtoRC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="NStoNC" formula ="{t}*({s}-{c})/{e}">
<SuperelevationAttainmentMethod>
Tento příklad definuje způsob výpočtu s názvem „AASHTO 2001 – Crowned Roadway“, při němž se používá standardní metoda odebrání nepříznivého vrcholového bodu dosažení klopení vozovky. Tento příklad zahrnuje výpočet pro vzdálenost přechodu nutnou pro dorovnání sklonu krajnice s jízdním pruhem (typ= „NKdoSS“).
Příklad způsobu výpočtu rovinného přechodu
Na tomto příkladu je ukázána směrově nerozdělená vozovka s jednostranným sklonem. Tato vozovka není střechovitá, neprovádí se tedy klopení vozovky ze střechy do dostředného sklonu.
Pro rovinný způsob výpočtu jsou vyžadovány dva vzorce: jeden pro oblouky, které jdou proti směru základního příčného sklonu, a druhý pro oblouky, které pokračují ve směru normálního příčného sklonu. Následující ilustrace ukazuje normalizované klopení vozovky, kde je vozovka bez klopení skloněna dolů zleva doprava. Oblouk vlevo proto vyžaduje delší přechod než oblouk vpravo:
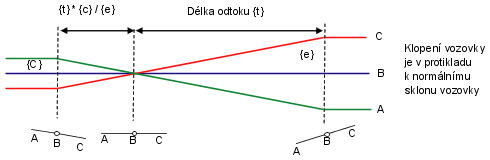
V následujícím příkladu definuje pokračující úsek délku jednostranného sklonu vzdálenosti klopení vozovky s normální korunou do plného klopení vozovky {t} (odvozeno z tabulek délek vzestupnic/sestupnic), mínus délka jednostranného sklonu krát standardní sklon vozovky {c} děleno plnou hodnotou klopení {e}. Druhý vzorec definuje vzdálenost od základního střechovitého sklonu vozovky do počátku oblouku jako procenta z {t} na základě proměnné {p} mínus {c} děleno {e}.
Opačný úsek definuje celkovou vzdálenost přechodu tak, aby se jednalo délku mezi rovnou korunou a plným dostředným sklonem {t}. Vzdálenost k počátku oblouku je dána jako procenta z {t} na základě proměnné {p} a vzdálenost mezi staničením základního střechovitého sklonu vozovky a rovné koruny je {t} * {c} / {e}
<SuperelevationAttainmentMethod name="Undivided Planar Roadway">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="{t}-{t}*{c}/{e}"/>
<TransitionFormula type="NCtoBC" formula="{t}*({p}-{c}/{e})"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula="{t}*{c}/{e}"/>
</Opposing>
<SuperelevationAttainmentMethod>
Přechod definovaný šířkou vozovky a Poměrem rozdílu sklonů na délku vzestupnice
Ne všechny organizace používají tabulky, které uvádějí délku náběhu přímo. Následující tabulka definuje plnou hodnotu klopení vozovky a 
jako funkci návrhové rychlosti a poloměru oblouku. V této situaci je hodnota použita k odvození délky náběhu založené na normální šířce vozovky. Tabulky délek náběhů definují hodnotu místo skutečné délky náběhu.
| Poloměr (m) | 90 km/h | 100 km/h | 110 km/h | 120 km/h | ||||
|---|---|---|---|---|---|---|---|---|
| E% |
|
E% |
|
E% |
|
E% | nepoužito | |
| 7000 | NC | nepoužito | NC | nepoužito | NC | nepoužito | NC | nepoužito |
| 5000 | NC | nepoužito | NC | nepoužito | NC | nepoužito | 2.0 | 0.31 |
| 3000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.3 | 0.32 |
| 1500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.2 | 0.33 | 3.0 | 0.33 |
| 1400 | 2.0 | 0.39 | 2.0 | 0.34 | 2.4 | 0.33 | 3.2 | 0.34 |
| 1300 | 2.0 | 0.39 | 2.0 | 0.34 | 2.6 | 0.33 | 3.5 | 0.34 |
| 1200 | 2.0 | 0.39 | 2.2 | 0.35 | 2.8 | 0.34 | 3.8 | 0.35 |
| 1000 | 2.0 | 0.39 | 2.6 | 0.36 | 3.7 | 0.35 | 4.5 | 0.37 |
| 900 | 2.2 | 0.40 | 2.9 | 0.37 | 3.7 | 0.36 | 5.0 | 0.38 |
| 800 | 2.5 | 0.40 | 3.3 | 0.38 | 4.2 | 0.38 | 5.7 | 0.39 |
| 700 | 2.9 | 0.41 | 3.7 | 0.39 | 4.8 | 0.39 | 6.0 | 0.40 |
| 600 | 3.4 | 0.42 | 4.4 | 0.41 | 5.6 | 0.41 | ||
| 500 | 4.0 | 0.44 | 5.2 | 0.43 | 6.0 | 0.42 | ||
| 400 | 5.0 | 0.46 | 6.0 | 0.45 | ||||
| 300 | 6.0 | 0.48 | ||||||
Následující příklad ukazuje metody a způsoby výpočtu založené na předchozí tabulce pro dva typy silnic. Proměnná {w} je šířka standardní vozovky od bodu klopení k hraně vozovky definovaná v průvodci klopením vozovky.
<SuperelevationAttainmentMethod name="Unspiraled ramp">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoBC" formula="{p}*{e}*{w}/{t}"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
</Opposing>
</SuperelevationAttainmentMethod>
<SuperelevationAttainmentMethod name="Unspiraled 2 way roadway">
<TransitionStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
<SuperelevationAttainmentMethod>