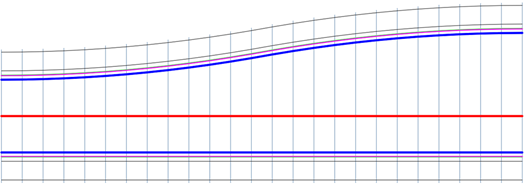
K vytváření a úpravám přechodů koridoru slouží panoramatický pohled Přechod koridoru.
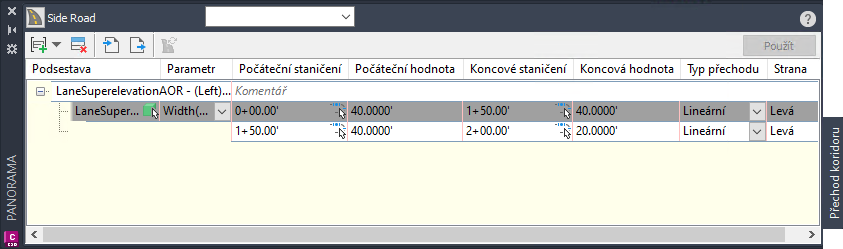
Když vyberete příkaz Upravit přechod koridoru, zobrazí se panoramatický pohled Přechod koridoru a na příkazovém řádku se zobrazí výzva k výběru podsestavy pro přechod.
Pomocí výzev na příkazovém řádku vyberte podsestavu a parametr pro přechod a poté také staničení, hodnoty a typ přechodu.
Hodnoty lze zadat také v panoramatickém pohledu Přechod koridoru.
Když vyberete řádek v panoramatickém pohledu, odpovídající přechod se ve výkresu zvýrazní modrými symboly.
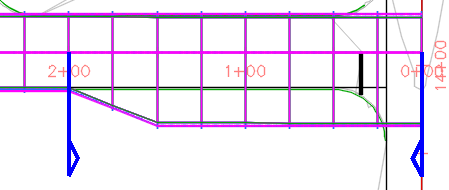
Typy přechodů
K dispozici je několik různých typů přechodů, které lze vytvořit.
Lineární
Jednoduchý lineární přechod, kde je každé vypočítané staničení založeno na následujícím vzorci:
Počáteční hodnota + ((vzdálenost od počátečního staničení / celková vzdálenost) * Delta)
Kde:
Delta = Hodnota koncového přechodu - hodnota počátečního přechodu
StationDelta = Vzdálenost od počátečního staničení / celková vzdálenost přechodu
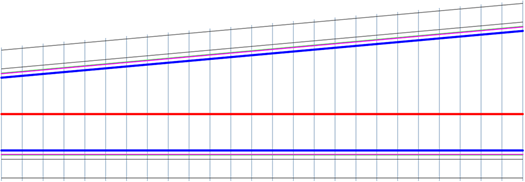
Zúžení stání
Přechod protisměrného oblouku, který používá následující vzorce:
Prvních 33,33 % vzdálenosti přechodu:
Počáteční hodnota + (((StationDelta * 3) ^ 2) * (Delta / 4))
Mezi 33,33 % a 66,66 % vzdálenosti přechodu:
Počáteční hodnota + (Delta / 4) + (((StationDelta * 3) - 1) * (Delta / 2))
Od 66,66 % do konce vzdálenosti přechodu:
Koncová hodnota - ((((1 - StationDelta) * 3) ^ 2) * (Delta / 4))
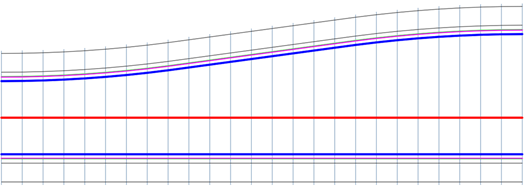
Kubické dovnitř
Kubický přechod s rozšířením na začátku přechodu a postupným zplošťováním směrem ke konci.
Tento přechod používá následující vzorec:
Koncová hodnota - (((1 - StationDelta) ^ 3) * Delta)
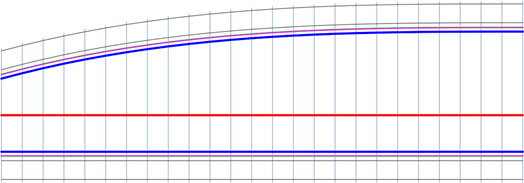
Kubické ven
Kubický přechod s rozšířením na konci přechodu a postupným zplošťováním směrem k začátku.
Tento přechod používá následující vzorec:
Počáteční hodnota + (StationDelta ^ 3) * Delta
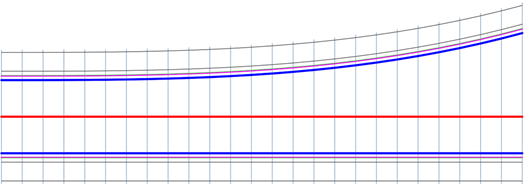
Parabolické dovnitř
Parabolický přechod s rozšířením na začátku přechodu a postupným zplošťováním směrem ke konci.
Tento přechod používá následující vzorec:
Koncová hodnota - (((1 - StationDelta) ^ 2) * Delta)
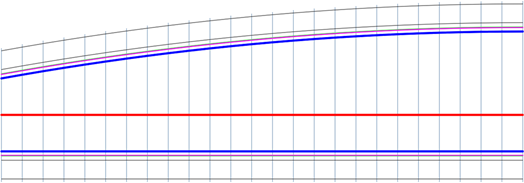
Parabolické ven
Parabolický přechod s rozšířením na konci přechodu a postupným zplošťováním směrem k začátku.
Tento přechod používá následující vzorec:
Počáteční hodnota + ((StationDelta) ^ 2 * Delta)

Reverzní parabolické
Reverzní parabolický přechod používá následující vzorce:
Pro prvních 50 % vzdálenosti přechodu:
Počáteční hodnota + (((StationDelta * 2) ^ 2) * (Delta / 2))
Od 50 % do konce vzdálenosti přechodu:
Koncová hodnota - ((((1 - StationDelta) * 2) ^ 2) * (Delta / 2))