Beschreibung eines thermischen Problems
Demonstrieren Sie die thermischen Funktionen von Helius PFA durch Evaluierung einer druckbelasteten Platte bei erhöhter Temperatur.
Es werden vier Methoden zum Modellieren der Materialreaktion verwendet und entworfen, um die wichtigen Faktoren hervorzuheben, die beim Einschließen von Temperaturauswirkungen in einer Simulation berücksichtigt werden sollten:
- Temperaturabhängiges Material mit thermischen Restspannungen auf Konstituentenebene, berechnet mit Materialeigenschaften in der aktuellen Temperaturumgebung (EP2_TD_ON_CURRENT_ENV.ans).
- Verwendet das im vorherigen Abschnitt erstellte Material.
- Temperaturabhängiges Material mit thermischen Restspannungen auf Konstituentenebene, berechnet mit Materialeigenschaften in einer angegebenen Temperaturumgebung (EP2_TD_ON_SPECIFY_ENV.ans).
- Verwendet das im vorherigen Abschnitt erstellte Material.
- Nicht temperaturabhängiges Material mit thermischen Restspannungen auf Konstituentenebene, berechnet mit Materialeigenschaften in der aktuellen Temperaturumgebung (EP2_non_TD_ON_CURRENT_ENV.ans).
- Verwendet ein Material, das mit den Eigenschaften bei 72 °F in der Tabelle im vorherigen Abschnitt charakterisiert wurde.
- Nicht temperaturabhängiges Material ohne thermische Restspannungen auf Konstituentenebene (EP2_non_TD_OFF.ans).
- Verwendet ein Material, das mit den Eigenschaften bei 72 °F in der Tabelle im vorherigen Abschnitt charakterisiert wurde.
Das Modell besteht aus einer Platte von 6 x 1.5 Zoll mit einer Lochbohrung von 0.125 Zoll in der Mitte der Platte und verwendet vollständig integrierte SOLID185-Elemente. Das Layup ist [45/-45/0/902]S und die Lagenstärke beträgt 0.005 Zoll. was zu einer Platte mit einer Dicke von 0.05 Zoll führt. Die Ausgangstemperatur der Platte wird mit 72 °F modelliert, und die Testtemperatur der Platte beträgt 140 °F. Im ersten Analyseschritt wird die Temperatur der Platte auf 140 °F erhöht, und im zweiten Schritt wird eine Drucklast mit gesteuerter Verschiebung auf die Platte bis zum endgültigen Ausfall angewendet. Es wird dringend empfohlen, die thermische Last in einem Schritt vor der mechanischen Belastung anzuwenden, da die wärmebedingte Verschiebung möglicherweise zu einer großen Veränderung der Lastverschiebungskurve führt, was die Interpretation der Lastverschiebungskurve erschweren kann. Die Lasten und Begrenzungsbedingungen werden in der folgenden Abbildung gezeigt. In der Abbildung ist die Lagenausrichtung von 0° an der globalen Y-Achse ausgerichtet.
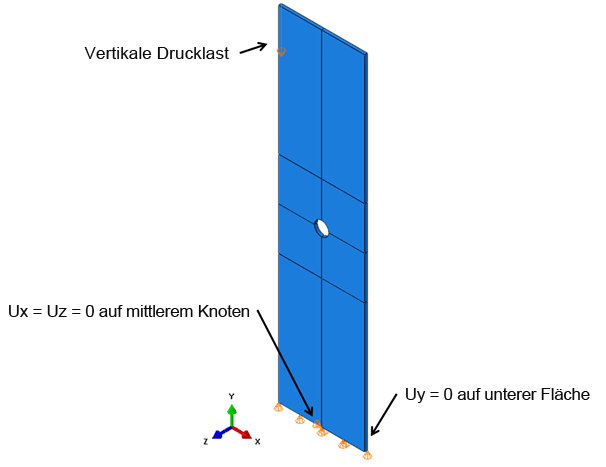
Die Werte der Modellausgangs- und -endtemperatur sind davon abhängig, ob die thermischen Restspannungen berücksichtigt werden. Wenn sie berücksichtigt werden, muss der Ausgangstemperaturwert identisch mit dem aktuellen Ausgangswert und die Endtemperatur identisch mit dem aktuellen Endwert sein. Dies ist darauf zurückzuführen, wie Helius PFA die Temperaturänderung ΔT von der spannungsfreien Temperatur bis zur Temperatur des Modells berechnet. Wenn die thermischen Restspannungen nicht berücksichtigt werden, sollte die Ausgangstemperatur des Modells 0 R betragen, und die Endtemperatur sollte die Temperaturänderung ΔT zwischen der Temperatur, bei der das Material charakterisiert wurde, und der Endtemperatur sein. Beispiel: Die unten stehende Tabelle listet Ausgangs- und Endtemperaturen für die vier Modelle in dem aktuellen Problem auf. Weitere Informationen zur Berechnung von ΔT finden Sie im Abschnitt Thermische Restspannungen im Theoriehandbuch.
| Material | Thermische Restspannung | Anfängliche Modelltemperatur | Endgültige Modelltemperatur | |
|---|---|---|---|---|
| Temperaturabhängig | Enthalten (aktuelle Umg) | 532 R (72 °F) | 600 R (140 °F) | |
| Temperaturabhängig | Enthalten (angegebene Umg) | 532 R (72 °F) | 600 R (140 °F) | |
| Charakterisiert bei 72 °F | Enthalten | 532 R (72 °F) | 600 R (140 °F) | |
| Charakterisiert bei 72 °F | Nicht verwenden | 0 R | 68 R (=140 °F - 72 °F) |
Die Eingabedateien für jedes Modell in diesem Beispielproblem stehen hier zur Verfügung. Wenn Sie eine dieser Dateien ausführen, stellen Sie sicher, dass die matID in der Eingabedatei der matID für das hier erstellte Material bzw. die hier erstellen Materialien entspricht.
Denken Sie daran, dass zum Aktivieren der Funktion der thermischen Restspannung in Helius PFA das Schlüsselwort *CURE STRESS zur HIN-Datei hinzugefügt werden muss. Um die Temperaturabhängigkeit zu aktivieren, legen Sie das neunte Argument des HELIUS-Befehls auf einen Wert von -1.0 fest.