Der letzte Teil des Puzzles zur Bestimmung der Verbundmaterial-Ermüdung besteht darin, die Geschwindigkeit des Bindungsbruchs mit dem makroskopischen Ausfall des Verbundmaterials zu verknüpfen.

Entwicklung des Schadensparameters

Wie bereits erwähnt, haben Hansen und Baker-Jarvis [36] die KTF mit makroskopischem Schaden verknüpft, indem sie einen Schadensparameter n einführten, der den Prozentsatz der Mikrorissdichte relativ zur Mikrorissdichte bei Ausfall repräsentiert. Die Schadensvariable, die den Anteil der für einen Bruch erforderlichen Mikrorissdichte darstellt, ist anfänglich gleich null und hat bei Ausfall den Wert 1. In ihrer Herleitung führten sie eine Differentialgleichung für die Entwicklung einer Schadensvariablen n mit der Zeit t ein, in der die Entwicklung der Schadensvariable direkt in Beziehung zur Bindungsbruchrate gebracht wird. Diese Methode prognostiziert erfolgreich die Festigkeit von Polymeren unter den Bedingungen einer großen Bandbreite von Spannungsraten.

Die von uns verwendete Differentialgleichung zur Beschreibung der Entwicklung von n ist derjenigen, die von Hansen und Baker-Jarvis vorgeschlagen wurde, sehr ähnlich:

In dieser Gleichung ist n 0 ein Parameter, der durch Erzwingung der folgenden Bedingung bestimmt wird:

während ni die Größe des Schadens zu Beginn der Dauerbelastung repräsentiert. Der Unterschied zwischen dieser Formel und der von Hansen und Baker-Jarvis besteht darin, dass ihre Formel λ = 1 voraussetzt. Dieser Wert ist der in unserer aktuellen Implementierung 2 verwendete Vorgabewert. Für den Fall λ = 1 ergibt sich

Unter der Annahme eines Werts von 1.0 für λ und durch Kombination der Gleichungen 57, 52 und 56 ergibt sich die Anfangsgleichung für die Berechnung der Dauerfestigkeit eines Polymers:

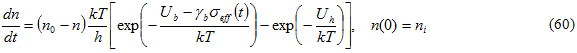
Die Lösung von Gleichung 61 liefert die zeitabhängige Entwicklung des Schadensparameters, die sich wie folgt darstellen lässt als 3:

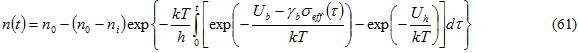
Gleichung 61 kann mit kalibrierten Werten für Ub, 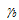und Uh verwendet werden, um den Zeitpunkt zu ermitteln, an dem der Schadensparameter den vollen Wert (n = 1) erreicht.

2 Für eine einzelne linear-elastische Analyse, d. h. keine progressive Fehleranalyse, ist die Wahl von λ irrelevant. Alle Lösungen von λ ergeben dieselbe Anzahl von Zyklen bis zum Ausfall. Dieser Faktor könnte jedoch sehr wichtig für die Simulation von Blockbelastungen und fortschreitendem Versagen sein.

3 Unser Darstellung in Gleichung 61 setzt voraus, dass U und T während des Ermüdungsprozesses konstant bleiben.