Charakterisierung der Materialien für Ermüdungsberechnung

Führen Sie die folgenden Schritte zum Charakterisieren von Material für die Ermüdungsberechnung aus.

Nach dem Festlegen der statischen In-situ-Eigenschaften (Festlegung der optimierten In-situ-Eigenschaften der Konstituenten) muss für jeden identifizierbaren Ermüdungsausfallmodus in der Verbundlage die folgende Charakterisierung der Materialien für die Ermüdungsberechnung ausgeführt werden. Die Vorgehensweise ist für jeden Modus identisch und wird daher nur einmal beschrieben. Der Charakterisierungsprozess des Materials für die Ermüdungsberechnung umfasst einen ersten Schritt gefolgt von einem iterativen Schritt. Die folgenden Verfahren definieren den ersten Schritt:

1. Lesen Sie die S-N-Kalibrierungskurven und die entsprechenden Parameter, R, f und T, sowie die Materialeigenschaften ein.
2. Drehen Sie die Spannung S im Hauptkoordinatensystem des Verbundwerkstoffs, um den Verbundspannungstensor σc zu ermitteln.
3. Extrahieren Sie den Matrixspannungstensor σm aus dem Verbundspannungstensor mit MCT.
4. Ordnen Sie den Matrixspannungstensor einer effektiven Spannung zu, wobei dies abhängig ist von der Mikrostruktur und davon, ob die Belastung entlang der Achse oder achsenverschoben auftritt.
5. Verwenden Sie den Wert R, um σeff,min = σeff,max zu berechnen.
6. Berechnen Sie die Mindestanzahl von Zyklen bis zum Ausfall mithilfe der Gleichung 61 und Schätzungen für Ub,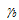, Uh und ψ
7. Nach Abschluss dieses ersten Schritts haben wir drei Vektoren σeff,max, σeff,min und Nf der Länge i, wobei i die Gesamtanzahl der Datenpunkte in der S-N-Kurve bzw. in den S-N-Kurven ist.

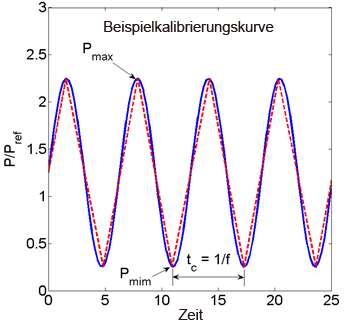
Der iterative Schritt der Materialcharakterisierung für die Ermüdungsberechnung umfasst die Anpassung von Ub,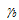, Uh und ψ zum Minimieren der Fehlerquote zwischen dem Protokoll der Zyklen bis zum Ausfall und dem Protokoll der prognostizierten Anzahl der Zyklen bis zum Ausfall. Die Durchführung dieser Aufgabe erfordert eine Annahme über den Belastungsverlauf. Wir nehmen an, dass die Belastung sägezahnförmig verläuft, wie unten durch die rote Kurve dargestellt. Wie bei den statischen In-situ-Eigenschaften wird das Gradientenverfahren des steilsten Abstiegs verwendet, um die Ermüdungsparameter zu optimieren.