Bestimmen Sie die durchschnittliche Matrixspannung, die zur Vorhersage der bindungsbrechenden und bindungsreparierenden Rate verwendet wird.

Prognostizieren Sie bei festgelegtem Spannungszustand oder Spannungsprotokoll eines Verbundwerkstoffs die bindungsbrechende Rate entsprechend Gleichung 40 und die bindungsreparierende Rate entsprechend Gleichung 41. Eine offensichtliche Herausforderung in diesem Prozess ist es, zu bestimmen, wie man den Matrixspannungstensor als eine effektive Skalarspannung darstellen kann, die mit den Gleichungen zur Beschreibung von KTF zu verwenden ist. Mehrere Forscher haben gezeigt: Ein geeigneter Parameter für die Vorhersage der Lebensdauer ist die Ermüdungsfestigkeit, die durch die statische Festigkeit unter der gleichen Belastungsbedingung normalisiert wurde [23, 44-45]. Dies wird im Englischen häufig als Strength-Life Equal Rank Assumption (SLERA) bezeichnet. Wir verwenden also die Funktion der statischen Ausfallkriterien zur Bestimmung einer effektiven Ermüdungsspannung.

Unidirektionale Verbundwerkstoffe

Unidirektionale Verbundwerkstoffe weisen zwei separate Modi (oder Prozesse) von Ermüdungsausfällen in der Lagenebene auf: achsenverschoben und entlang der Achse. Jeder Vorgang muss über eine eigene Aktivierungsenergie und ein eigenes Aktivierungsvolumen verfügen, da die physikalischen Eigenschaften der Akkumulation von Mikrorissen für die beiden Arten von Rissbildung unterschiedlich sind. Außerdem sind die effektiven Spannungsdefinitionen unterschiedlich. In diesem Abschnitt definieren Sie die effektive Matrixspannung für die achsenverschobene Belastung und die Belastung entlang der Achse.

Achsenverschoben

Bei der Form des Ausfallkriteriums ist es hilfreich, die in dem Experiment beobachteten achsenverschobenen Ausfallmodi zu berücksichtigen. Es wurde häufig berichtet, dass Ermüdungsausfälle oft über parallel zu Fasern verlaufende Risse [24, 46] bei unidirektionalen Verbundwerkstoffen auftreten. Daher ist anzunehmen, dass die Zugkräfte lotrecht zu den Fasern wie auch die Scherspannungen auf diesen Ebenen eine wesentliche Rolle bei der Ermüdung spielen. Bei einer axialen Faserrichtung von 1- empfehlen wir ein lokales Matrixausfallkriterium in Form von transversalen isotropen Invarianten des Matrixspannungstensors, berechnet mit MCT in der Form

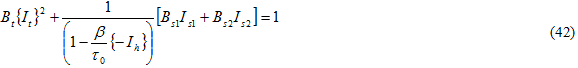
dabei gilt:

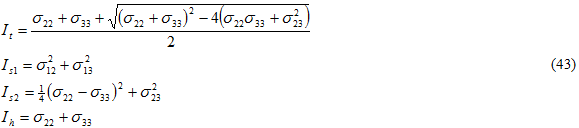
und die {} Macaulay-Klammern bezeichnen, sodass der Wert null ist, wenn die eingeschlossene Größe negativ ist. Die Werte für Bi werden anhand von drei statischen Ausfalltests für den Verbundwerkstoff bestimmt: Querzug, Querdruck Scherung in der Ebene. Jeder Test umfasst den Ausfall der Matrixkonstituente. Durch Teilen der Gleichung 42 durch Bs1 erhalten Sie eine Form für eine effektive Spannung σ eff

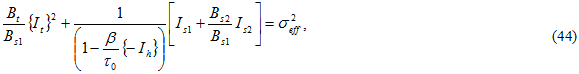
wobei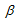 ein Druckverstärkungskoeffizient und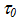die Matrixscherfestigkeit ohne Druckverstärkung ist. In der aktuellen Version verwenden alle Berechnungen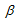= 0. Durch das Ziehen der Quadratwurzel aus Gleichung 44 erhalten Sie die effektive Spannung für die Berechnung der bindungsbrechenden Rate entsprechend der Gleichungen 40 und 41.

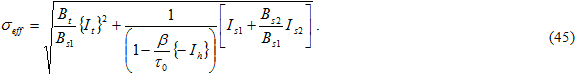
Entlang der Achse

Belastungsausfälle entlang der Achse ergeben sich aus Matrixrissen, die an der Schnittstelle von Faser und Matrix auftreten. Diese Risse entstehen hauptsächlich durch normale Spannungen in axialer Richtung. Daher wird bei Ausfällen entlang der Achse (θ = 0°) die effektive Spannung definiert als