Thermisch aktivierte Prozesse
Erfahren Sie, wie KTF von thermisch aktivierten Prozessen beeinflusst wird.
Alle Atome und Moleküle oszillieren bei Temperaturen über dem absoluten Nullpunkt mit einer Frequenz proportional zu n 0 gemäß dem Plankschen Gesetz
Hierbei bezeichnet h die Plancksche Konstante (h = 6,626068 x 10-34 J-s/K-Atom ) und kT die thermische Energie, ausgedrückt als Produkt der Boltzmann-Konstante k (k = 1,3806504 x 10-23 J/K-Atom) und der absoluten Temperatur T. Da jedoch die mit jeder Schwingung verbundene thermische Energie tatsächlich keine einzelne Zahl, sondern vielmehr eine Verteilung darstellt, besteht immer die Möglichkeit, dass jede Schwingung über ausreichend Energie verfügt, um die Energiebarriere U zu überwinden und von einem Gleichgewichtszustand in einen anderen zu wechseln. Die Wahrscheinlichkeit, dass dies für eine gegebene Schwingung eintrifft, wird durch die vertraute exponentielle Form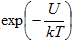 
ausgedrückt. Damit lässt sich die Bindungsbruchrate K b in einfacher Form wie folgt beschreiben:
Für die Zwecke der Bruch- und Ermüdungsberechnung ist der eine Gleichgewichtszustand als der Zustand ohne Bindungsbruch und der andere als der Zustand nach Bindungsbruch aufzufassen. Der Prozess wird in der linken Abbildung unten schematisch dargestellt. Die Bindungsheilung kann mit einer ähnlichen Gleichung beschrieben werden:
Betrachten wir nun die Auswirkungen der angewendeten Spannung auf die Bindungbruchrate in Gleichung (38) und die Bindungsheilungsrate in Gleichung (39). In diesem Zusammenhang ist es hilfreich, sich die Spannung als Energie pro Volumeneinheit statt als Kraft pro Flächeneinheit vorzustellen. Wenn die Spannung den Bindungsbruchprozess befördern soll, sollte sie die Energiebarriere für den Bindungsbruch erhöhen und die für die Bindungsheilung erforderliche Energiebarriere verringern.
Die Differenz hängt ab vom Volumen des Materials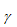 
, dem Aktivierungsvolumen, über das der Vorgang erfolgt 1, sodass die Verringerung der Aktivierungsenergie sich als das Produkt von Aktivierungsvolumen und Spannung ergibt. Die Abbildung auf der rechten Seite illustriert, wie die Spannung die Aktivierungsenergie modifiziert. Für die Gleichung (38) ergibt sich folgende abgewandelte Form, um die Auswirkung einer angewendeten Spannung zu berücksichtigen:
Analog für Gleichung 39
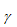fallen für Bindungsbruch und Bindungsheilung unterschiedlich aus, da die Aktivierungsenergien und Aktivierungsvolumina für diese beiden Prozesse physikalisch verschieden sind. Die Gleichungen 40 und 41 sind die Grundgleichungen für die KTF, die von Helius PFA zur Prognose von Verbundmaterial-Ermüdung verwendet werden.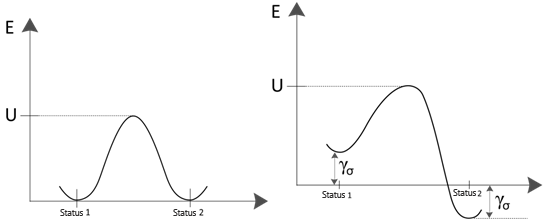
1 Die genaue Definition des Aktivierungsvolumens ist für den Prozess des Polymerbruchs etwas mehrdeutig, da es weit größer ist als z. B. das Atomvolumen. Daher wird es in der Regel nur als das Volumen definiert, das von dem aktivierten Prozess betroffen ist.