Entwickeln Sie die Beziehungen für einen Verbundwerkstoffs aus zwei Konstituenten (Faser und Matrix).

In einer Analyse auf struktureller Ebene haben wir an jedem Materialpunkt in der Struktur des Verbundwerkstoffs direkten Zugriff auf die mittleren Spannungs- und Dehnungszustände des Verbundwerkstoffs (σc und εc). In diesem Abschnitt entwickeln wir die Beziehungen für einen Verbundwerkstoff aus zwei Konstituenten (Faser und Matrix), sodass εc in die mittleren Spannungs- und Dehnungszustände (σf, εf, σm, εm) der Konstituente zerlegt werden. Der Rahmen für diese MCT-Zerlegung wird durch die Gleichungen 4 und 8 des vorherigen Abschnitts bereitgestellt, die für alle Materialreaktionen und alle Ebenen der Verformung gültig sind.

Der erste Schritt in der Entwicklung der MCT-Zerlegung besteht darin, geeignete konstitutive Beziehungen aufzurufen, die die mittleren Spannungsmaße bezogen auf die entsprechenden durchschnittlichen Dehnungsmaße ausdrücken. Wir legen die Einschränkung fest, dass konstitutive Beziehungen linear sind, sodass die MCT-Zerlegung eindeutig und mathematisch lenkbar bleibt. Wir werden später sehen, dass die Einschränkung auf lineare konstitutive Beziehungen keine schwerwiegende Einschränkung darstellt; die MCT-Zerlegung kann weiterhin bei nicht linearen Problemen verwendet werden. Die Gleichungen 12-14 listen die verschiedenen volumengemittelten, linearisierten konstitutiven Beziehungen auf, die verwendet werden.

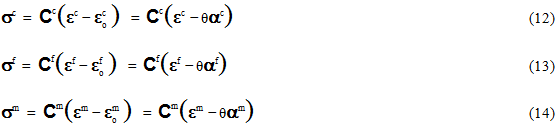
In den Gleichungen 12-14 stellen Cc, Cf und Cm die konstitutiven 6-x-6-Matrizen (Sekantenformulierung) für den homogenisierten Verbundwerkstoff, die Faser- bzw. die Matrixkonstituentenmaterialien dar. θ stellt eine gleichmäßige Temperaturänderung des Verbundmaterials relativ zur gleichmäßigen Referenztemperatur dar, bei der Materialeigenschaften gemessen wurden. Die Terme αc, αf und αm sind 6-x-1-Vektoren, die thermische Koeffizienten der Ausdehnung für die homogenisierten Verbund-, Faserkonstituenten- und Matrixkonstituentenmaterialien darstellen. Da die konstitutiven Beziehungen linear sind, sind die einzelnen Komponenten Cc, Cf, Cm, αc, αf und αm einfach Konstanten. Zum Anwenden der MCT-Zerlegung auf nicht lineare Probleme wird davon ausgegangen, dass die konstitutiven Beziehungen (Gleichungen 12-14) über den aktuellen Zustand (definiert durch σc, εc, σf, εf, σm, εm und θ) linearisiert sind. Dieser Ansatz ist vollständig kompatibel mit dem Ansatz, der häufig bei nicht linearen Analysen auf struktureller Ebene verwendet wird, bei denen eine insgesamt nicht lineare Antwort einer Verbundstruktur durch eine Abfolge von stückweise linearen Reaktionen dargestellt wird.

Als Nächstes werden die linearisierten konstitutiven Beziehungen (Gleichungen 12-14) in Gleichung 4 ersetzt. Ergebnis:

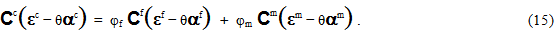
Wenn weiterhin Gleichung 8 durch Gleichung 15 ersetzt wird, ergibt dies

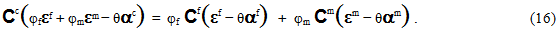
Gleichung 16 kann nun für den durchschnittlichen Dehnungszustand der Faser (εf) gelöst werden, indem ähnliche Terme gruppiert und alle Terme mit 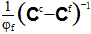multipliziert werden. Ergebnis:

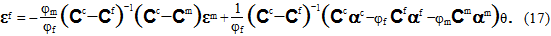
An diesen Stelle können Sie mühelos die Beschränkung bei den zuvor erzwungenen linearisierten konstitutiven Beziehungen nutzen. Insbesondere, wenn die Komponenten Cc, Cf, Cm, αc, αf und αm keine Konstanten sind, ist die Algebra, die zu Gleichung 17 führt, unlösbar.

Um Ihnen die Arbeit zu erleichtern, definieren wir nun wie folgt eine 6-x-6-Matrix A und einen 6-x-1-Vektor a.

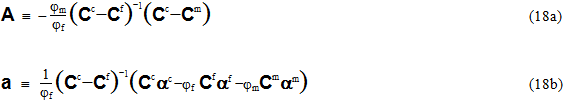
Mit diesen neu definierten Mengen kann Gleichung 17 einfach wie folgt geschrieben werden:

Beachten Sie, dass die Matrix A die durchschnittlichen mechanischen Dehnungen in den Konstituenten in Beziehung setzt, während der Vektor a die durchschnittlichen thermalen Dehnungen in den Konstituenten in Beziehung setzt. Gleichung 19 kann nun verwendet werden, um die durchschnittliche Faserdehnung εf aus Gleichung 8 zu entfernen, was zu einem Ausdruck für den durchschnittlichen Dehnungszustand εm der Matrix führt, und zwar in Bezug auf den durchschnittlichen Dehnungszustand des Verbundwerkstoffs εc.

Sobald der durchschnittliche Dehnungszustand der Matrix εm über die Gleichung 20 berechnet wurde, kann der durchschnittliche Dehnungszustand der Faser εf einfach mit Gleichung 8 wie folgt berechnet werden:

Nach der Berechnung der durchschnittlichen Dehnungszustände sowohl der Matrix als auch der Faser (εm und εf) können die durchschnittlichen Spannungszustände von Matrix und Faser (σm und σf) mit den linearisierten konstitutiven Beziehungen berechnet werden (Gleichungen 13 und 14).

Zusammenfassend lässt sich sagen, dass die analytische Form der MCT-Zerlegung aus vier Gleichungen besteht (Gleichungen 20, 21, 13 und 14). Diese werden verwendet, um einen durchschnittlichen Dehnungszustand eines Verbundwerkstoffs an einem Materialpunkt in einzelne durchschnittliche Spannungs- und Dehnungszustände an demselben Materialpunkt zu zerlegen. Diese Zerlegung kann sehr effizient innerhalb einer Verbundstruktur an jedem beliebigen Punkt durchgeführt werden, dessen durchschnittliche Dehnungszustände des Verbundwerkstoffs bekannt ist. Die MCT-Zerlegung ist eine Basistechnologie, die mehr physische Einblicke in den Zustand der heterogenen Mikrostruktur von Verbundwerkstoffen bietet. Wie wir später sehen werden, besteht der wichtigste Vorteil der Kenntnis über die mittleren Spannungs- und Dehnungszustände der Konstituente in einer verbesserten physikalischen Basis, über die die Schadensentwicklung und der Materialausfall in den Konstituentenmaterialien der Verbund-Mikrostruktur vorhergesagt werden können.

Die grundlegende Gleichung der MCT-Zerlegung wird durch die Gleichung 20 vorgegeben. Diese kann man sich als eine Übertragungsfunktion vorstellen, die einen durchschnittlichen Dehnungszustand εc eines Verbundstoffs dem durchschnittlichen Dehnungszustand εm zuordnet. Es lohnt sich, die Auswirkungen der Verwendung von Gleichung 20 bei einem Verbundmaterial, das ein nicht lineares Verhalten aufweist, zu wiederholen. Zunächst wird die Abbildung von εc auf εm vollständig von den Mengen Cc, Cf, Cm, αc, αf, αm, φf und φm definiert, die als konstant angenommen werden. Aus diesem Grund müssen für nicht lineares Materialverhalten oder finite Verformungen die konstitutiven Beziehungen (Gleichungen 12-14) zum aktuellen Materialzustand linearisiert werden (definiert durch σc, εc, σf, εf, σm, εm und θ). Die Auswirkungen dieser Beschränkung ist, dass die gesamte nicht lineare Reaktion des Verbundmaterials durch eine endliche Reihe linearer Reaktionen dargestellt werden muss, wobei Cc, Cf, Cm, αc, αf und αm als Konstante innerhalb jedes Segments der Reaktion betrachtet werden können. In der Realität unterscheidet sich die MCT-Zerlegung für jedes Segment der Reaktion, da sich Cc, Cf, Cm, αc, αf und αm von einem Segment zum nächsten ändern. Diese stückweise lineare Darstellung der Materialreaktion ist vollständig kompatibel mit der Methode, die häufig beim Durchführen von nicht linearen Analysen auf struktureller Ebene verwendet wird.

Es sollte auch betont werden, dass die MCT-Zerlegung (zusammen die Gleichungen 20, 21, 13, 14) minimalen rechnerischen Aufwand erfordert. Daher kann sie bei einer Analyse auf struktureller Ebene bei allen Interessensgebieten angewendet werden, ohne dass sich die Berechnungszeit insgesamt wesentlich erhöht. Beispiel: In einer Finite-Elemente-Analyse auf struktureller Ebene einer Verbundstruktur erhöht sich bei Verwendung der MCT-Zerlegung an jedem Gaußschen Integrationspunkt im Modell in der Regel nur die Gesamtlösungszeit um 2 % - 3 %.

Die analytische binäre Zerlegung ist besonders für einfache, unidirektional faserverstärkte Verbundmaterialien vorteilhaft. Helius PFA verwendet die analytische binäre Zerlegung für alle unidirektionalen verstärkten Verbundmaterialien. Auch für gewebte oder geflochtene Verbundwerkstoffe wird die endgültige Zerlegung von der mittleren Spannung und Dehnung des Garns zur mittleren Spannung und Dehnung von Faser und Matrix mithilfe der analytischen binären Zerlegung durchgeführt.