The final portion of the cohesive constitutive relation that must be defined is the expression for the evolution of the scalar damage variable D.

The damage evolution model must be capable of accurately expressing the evolution of the damage variable D from its initial value of 0 to its final value of 1 regardless of the exact history of combined loading sustained by the cohesive material. Note, it is possible to develop a damage evolution model expressed in terms of strains (i.e., relative displacements) or stresses, but for our initial implementation, we adopt a strain-based (relative displacement) approach. It is logical and perhaps intuitive to hypothesize that damage evolution is affected differently by normal and shearing relative displacements. However, for the sake of simplicity, we assume that damage evolution can be expressed as a function of a single scalar measure of relative displacement (referred to as the effective relative displacement 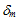), where

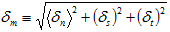
The corresponding effective traction will be defined as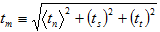

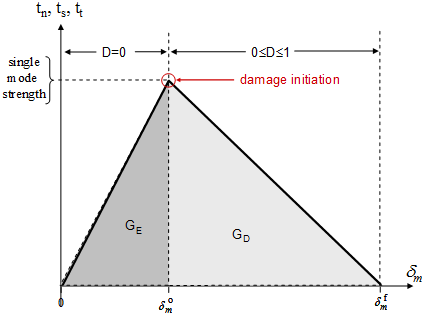
In the graphic above, 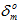denotes the value of the effective relative displacement 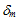at damage initiation, e.g., at the time when

becomes satisfied. 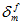denotes the value of the effective relative displacement 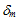at which the material stiffness has fully degraded to zero. 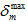denotes the maximum value of the effective relative displacement 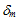that has been attained by the material to date for any time t less than or equal to the current time. Note that 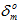and 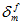are considered to be part of the material characterization.

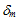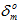
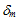
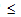
For any values of within the range 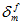, the current value of damage variable D can be expressed via the following damage evolution equation.

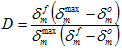
It should be emphasized that the main difference among the three cohesive constitutive models provided in Helius PFA concerns the precise manner in which 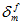is computed for the purpose of evaluating damage evolution. For the total displacement model, the value of 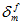is computed by simply adding the effective relative displacement at damage initiation 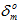to the user-specified parameter ( 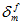- 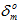). Thus, once damage initiation occurs and 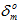is known, the effective relative displacement at complete material degradation (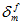) remains fixed even if the combined load state of the cohesive material changes.

To understand how 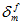is computed for the total energy model or the mixed mode power law, we must first define some energy expressions. At any point in time, the individual energy components associated with normal and shearing deformations are defined as

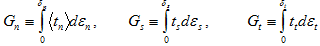
The total energy absorbed by the cohesive material is simply the sum of the three energy components

Gtotal = Gn + Gs + Gt

When the total energy Gtotal reaches the critical total energy value 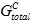, the cohesive material has fully degraded to zero stiffness and can no longer support any load. Thus, knowing the critical total energy value 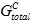, we can compute the effective relative displacement 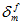when the cohesive material reaches complete degradation as shown below.

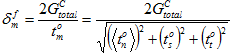
For the total energy model, 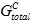never changes. It is the same user-specified constant regardless of the instantaneous mix of tractions applied to the cohesive material. For the mixed mode power law, the value of 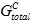continually changes in response to the changing mix of traction components that act on the cohesive material. In the mixed mode power law, the instantaneous value of 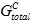can be obtained by uniformly scaling the instantaneous values of Gn, Gs, and Gt upwards until the following criterion is met.

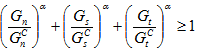
Given any instantaneous set of tractions (tn, ts, tt) and their instantaneous individual energy density components (Gn, Gs, Gt), we can use the above criterion and uniformly scale these tractions upwards to the level where the criterion is met. Let us denote this scaled traction as (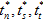) and their corresponding scaled energy components as (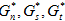). Given the projected energy components (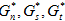) that would result in delamination propagation, we can now calculate the total energy that would result in delamination propagation as .