Use the constituent average stress states to independently identify damage initiation.

In the energy-based material degradation scheme, Helius PFA uses constituent average stress states to independently identify damage initiation in the matrix and fiber constituents. The matrix and fiber damage initiation criteria are the same as the constituent failure criteria described earlier (Matrix Constituent Failure Criterion and Fiber Constituent Failure Criterion). Once damage initiates within the matrix or fiber constituent, the appropriate scalar damage variable (D m for matrix, or D f for fiber) begins evolving from zero to unity. The damage variables (D m and D f ) serve as stiffness reduction factors for the various composite moduli as shown below.

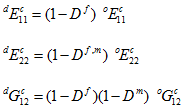
In the expressions for the damaged composite moduli above, the pre-superscript d indicates the quantities are degraded (or damaged) quantities, while the pre-superscript o indicates the quantities are original (un-damaged) quantities. In the above equations Df,m is understood to represent Dm if Dm > 0; otherwise, Df,m is understood to represent Df.

Note how the damaged shear modulus is dependent on both Dm and Df. This forces the shear modulus to degrade nonlinearly if both constituents have failed. It enforces a strictly decreasing function for the degradation, which ensures the energy dissipated is always positive.

Once damage initiation occurs for one or both constituent materials, we must have an expression for constituent damage evolution applicable to any strain state the material might exhibit. For this purpose, it is practical to utilize an effective scalar measure of stress and strain appropriate for each of the constituents (fiber and matrix). For predicting damage evolution within the matrix constituent, we define an effective stress and strain as follows.

effective stress for the matrix: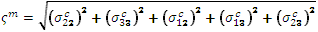

effective strain for the matrix: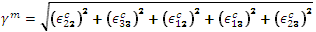

For predicting damage evolution within the fiber constituent, we define an effective stress and strain as follows.

effective stress for the fiber: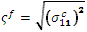

effective strain for the fiber: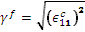

It should be emphasized that these effective matrix and fiber values are computed directly from the composite average stress and strain components, without having to resort to MCT decomposition.

The evolution of the constituent damage variables is expressed in terms of these effective strains as shown below.

Df is the fiber damage variable (0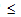Df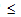1) and is computed by

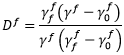
where is the value of at damage initiation, and is the value of when the material becomes fully degraded (reaches zero stiffness).

Dm is the matrix damage variable (0Dm1) and is computed by

where 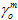is the value of 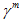at damage initiation, and is the value of 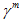when the material becomes fully degraded (reaches zero stiffness).

It should be re-emphasized that the dissipated energy of a fully degraded material is directly proportional to and 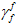. Consequently, mesh sensitivity is alleviated by making and 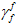proportional to element size, as given by

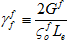
where Gm and Gf are the composite energy densities dissipated when the matrix and fiber constituents reach their fully degraded conditions. 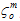and 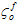are the effective stresses at matrix and fiber damage initiation respectively, and Le is the effective element length.

Discrete Interval Partitioning

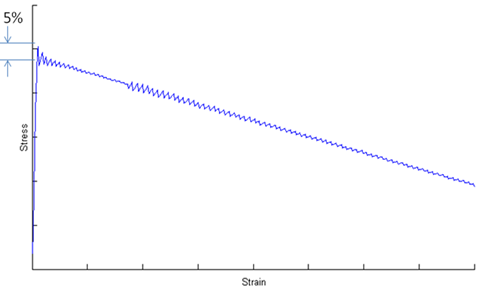
The Energy-Based damage feature of Helius PFA uses multiple discrete intervals when linearly degrading the composite, as shown below. Each interval uses a secant modulus to define the response of the composite in that specific interval. For problems where the total energy represents something similar to an isosceles triangle, the intervals will accurately capture the response of the composite.

For analyses where the total energy represents a very heavily skewed triangle, as shown below, interval partitioning will not accurately capture linear softening of the composite at early strain levels. This is entirely due to the number of intervals used to achieve the most rapid and robust convergence of the problem. Specifically, the stress secant intervals at strain levels near failure retain a high stiffness and can cause a misrepresentation of the stress state of the composite. If you have analyses that define a linear degradation curve with a final effective strain over 100 times the initial effective strain, please contact Autodesk for support.