Introduction to Energy-Based Damage Evolution

View the energy-based damage evolution formulation.

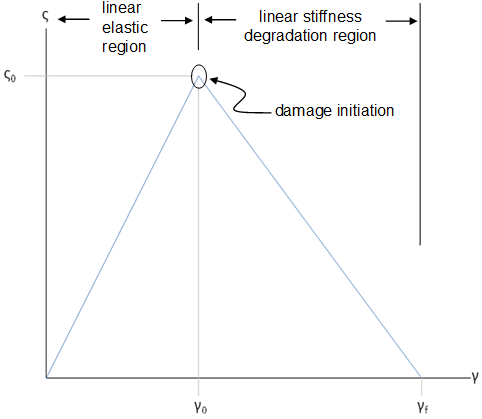
The simplest possible constitutive relation that permits the rate of material degradation to be controlled is a bi-linear law composed of a linear elastic region followed by a linear stiffness degradation region as shown below. In this graphic, ς0 represents an effective measure of composite stress at failure initiation. γ0 represents an effective measure of composite strain at failure initiation. γf represents an effective measure of composite strain at which damage has fully evolved and the material stiffness has been completely degraded to zero, preventing the material from carrying any load.

Now consider the total energy G that has been dissipated by a completely degraded element of volume V e . For the simple constitutive relation shown above, this total dissipated energy can be expressed as

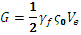
where γf is the final value of a measured effective strain, and ς0 is a value of measured effective stress at the initiation of failure.

The key to alleviating mesh sensitivity associated with progressive failure results is to keep the total energy dissipation constant, regardless of the element size. This constant energy dissipation can be achieved by appropriately controlling ς0 or γf as functions of element size. For the purposes of failure analyses, changing the value of ς0 would effectively change the stress at which a composite material is said to fail. This is intuitively un-appealing, so the most obvious choice is to change γf such that the energy G is conserved for varying element sizes as

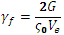
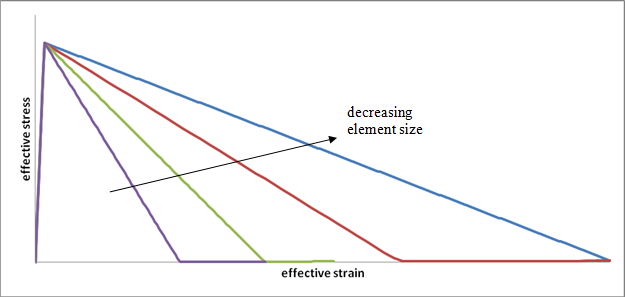
The graphic below shows the resulting family of constitutive laws obtained for a single accepted value of G as the element size is changed.