Constituent Average Stress and Strain States
This section introduces the concept of constituent average stress and strain states for both unidirectional and woven composites.
Simple derivations of these quantities are developed, and the advantages and limitations of using constituent average quantities are discussed.
Let σ(x,y,z) denote the actual stress tensor field that varies with respect to position within each of the constituent materials of the heterogeneous microstructure. Let D denote the domain of a representative volume element (RVE) sufficient for characterizing the composite material response at a point. Regardless of the complexity of the actual stress distribution within the RVE, the composite average (or homogenized) stress state σc within the RVE can be expressed as

where V is the total volume of the RVE. Similarly, the fiber and matrix average stress states can be expressed as

where Vf and Vm are respectively the volumes of the fiber and matrix constituents within the RVE (V=Vf +Vm), and Df and Dm denote respectively the subdomains occupied by the fiber and matrix constituents within the RVE (D = Df 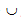 Dm). Combining Eqs. 1-3 yields
Dm). Combining Eqs. 1-3 yields

where φf = Vf/V and φm = Vm/V are volume fractions of the fiber and matrix constituent materials respectively.
Similar reasoning can be applied to the strain tensor yielding Eqs. 5-8 below.

The fundamental argument for the use of Multicontinuum Theory is that constituent average stress and strain states (σf, σm, εf, εm) are much more relevant in predicting damage evolution and material failure than composite average stress and strain states (σc, εc). Damage evolution and failure in the matrix constituent is physically driven by the stress and strain in the matrix constituent material, not the stress and strain in the fiber constituent material, nor the stress and strain in the homogenized composite material. A similar argument could be stated for the fiber constituent.
While it is easy to appreciate that averaging the actual micromechanical stress field over individual constituents provides superior information with which to predict damage evolution and failure in composites, it is informative to consider the filtering characteristics of the volume averaging process as it pertains to the various average stress states. Let us begin by considering a representative volume element of a unidirectional fiber-reinforced composite material subjected to a simple homogenized composite stress state σc. For example, a uniaxial stress state where  > 0 and all other
> 0 and all other 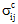 = 0. Even though the composite average stress state is uniaxial, the actual micromechanical stress field σ(x,y,z) within the heterogeneous microstructure of the RVE is quite complex. This is due to self-equilibrating interactions between the constituent materials caused by differences in their stiffnesses, Poisson ratios, and thermal expansion coefficients. For example, in the actual micromechanical stress field, four of the six stress components ( σ11, σ22, σ33, σ23) achieve non-zero values within the RVE. Furthermore, these four stress components exhibit a high degree of spatial variation over the RVE with numerous localized stress concentrations. However, three of the actual stress components ( σ11, σ33, σ23) are due entirely to self-equilibrating interactions between the constituent materials. For example, differences in the Poisson ratios of the fiber and matrix are responsible for the development of self-equilibrating σ11(x,y,z) and σ33(x,y,z) fields. In the presence of spatially varying σ11(x,y,z), σ22(x,y,z) and σ33(x,y,z) fields, shear stress must develop to maintain local equilibrium. Equations 9-11 show the partial differential equations of equilibrium that have been simplified for the present case of a unidirectional composite RVE where all stress components are constant with respect to the fiber direction (i.e., the '1' direction).
= 0. Even though the composite average stress state is uniaxial, the actual micromechanical stress field σ(x,y,z) within the heterogeneous microstructure of the RVE is quite complex. This is due to self-equilibrating interactions between the constituent materials caused by differences in their stiffnesses, Poisson ratios, and thermal expansion coefficients. For example, in the actual micromechanical stress field, four of the six stress components ( σ11, σ22, σ33, σ23) achieve non-zero values within the RVE. Furthermore, these four stress components exhibit a high degree of spatial variation over the RVE with numerous localized stress concentrations. However, three of the actual stress components ( σ11, σ33, σ23) are due entirely to self-equilibrating interactions between the constituent materials. For example, differences in the Poisson ratios of the fiber and matrix are responsible for the development of self-equilibrating σ11(x,y,z) and σ33(x,y,z) fields. In the presence of spatially varying σ11(x,y,z), σ22(x,y,z) and σ33(x,y,z) fields, shear stress must develop to maintain local equilibrium. Equations 9-11 show the partial differential equations of equilibrium that have been simplified for the present case of a unidirectional composite RVE where all stress components are constant with respect to the fiber direction (i.e., the '1' direction).

Equations 10 and 11 imply that shear stress component σ23 must evolve at any point within the RVE where  or
or 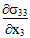 are non-zero. Unfortunately, these self-equilibrating stress components (σ11, σ33, σ23) are completely filtered out by the process of averaging the micromechanical stress field over the entire RVE, thus the composite average stress state is uniaxial with
are non-zero. Unfortunately, these self-equilibrating stress components (σ11, σ33, σ23) are completely filtered out by the process of averaging the micromechanical stress field over the entire RVE, thus the composite average stress state is uniaxial with  > 0.
> 0.
This inability of the composite average stress state σc to represent self-equilibrating stress components is best exemplified in the case of an unconstrained composite material subjected to a uniform temperature change. In this case, all four non-zero components (σ11, σ22, σ33, σ23) of the actual stress field σ(x,y,z) are self-equilibrating and caused by differences in the thermal coefficients of expansion of the two constituent materials. The composite average stress state is identically zero (σc= 0). However, for large temperature changes, the non-zero components (σ11, σ22, σ33, σ23) of the actual micromechanical stress field σ(x,y,z) may be large enough to actually cause damage evolution or material failure.
In contrast to the stringent filtering that occurs during the calculation of composite average stress states, the process of computing constituent average stress states only filters out stress components that are self-equilibrating over that particular constituent material. It should be emphasized that self-equilibrating normal stresses driven by differences in constituent Poisson ratios or thermal coefficients of expansion are self equilibrating over the RVE as a whole, but not self-equilibrating over any one constituent. Therefore, the constituent average stress states do not filter out these self-equilibrating normal stresses. On the other hand, the self-equilibrating shear stresses that develop to maintain local equilibrium are self-equilibrating even within each individual constituent material. Consequently, both the composite average stress states and the constituent average stress states filter out the self-equilibrating shear stresses.
Based on the previous discussion, the following list summarizes the filtering characteristics of constituent average stress states.
In general, the application of one or more composite average normal stresses (e.g.,
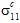 ,
,  , and/or
, and/or 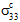 ) yields constituent average stress states that are triaxial (i.e., all three normal stresses are non-zero). This observation is true even if the composite stress state is uniaxial (e.g.,
) yields constituent average stress states that are triaxial (i.e., all three normal stresses are non-zero). This observation is true even if the composite stress state is uniaxial (e.g., 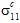 ≠ 0, and all other
≠ 0, and all other 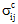 = 0). This is a direct result of the Poisson interactions between constituent materials. Normal stresses generated by differences in Poisson ratios of the constituents are self-equilibrating when integrated over the entire RVE, but are not self-equilibrating when integrated over a single constituent. Consequently, the constituent average stress state retains both the normal stresses that result from external mechanical loading and normal stresses caused by Poisson interactions between the constituents.
= 0). This is a direct result of the Poisson interactions between constituent materials. Normal stresses generated by differences in Poisson ratios of the constituents are self-equilibrating when integrated over the entire RVE, but are not self-equilibrating when integrated over a single constituent. Consequently, the constituent average stress state retains both the normal stresses that result from external mechanical loading and normal stresses caused by Poisson interactions between the constituents.When an unconstrained composite material is subjected to a uniform temperature change, differences in the thermal expansion coefficients of the constituents cause the development of self-equilibrating thermal stresses when integrated over the entire RVE, but not self-equilibrating when integrated over a single constituent. In this case, the composite average stress state is identically zero (σc = 0). However, the constituent average stress states are triaxial (i.e.,
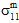 ≠ 0,
≠ 0, 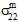 ≠ 0,
≠ 0, 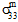 ≠ 0,
≠ 0, 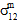 =
= 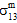 =
= 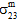 = 0 and
= 0 and 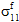 ≠ 0,
≠ 0, 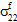 ≠ 0,
≠ 0, 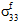 ≠ 0,
≠ 0, 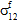 =
= 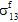 =
= 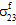 = 0).
= 0).Unidirectional fiber reinforced composite materials are orthotropic (or transversely isotropic) and consequently do not exhibit coupling between normal and shear stresses. Generally speaking, there are two different means by which shear stresses are generated in composite materials. First, externally applied mechanical loads can generate shear stresses in the composite material, and these shear stresses are not self-equilibrating. Consequently, both the composite average stress state (σc) and the constituent average stress states (σf and σm) contain measures of these shear stresses. Second, self-equilibrating shear stress fields are generated to maintain local equilibrium in the presence of normal stresses that exhibit spatial variation within the RVE (as per the partial differential equations). These shear stresses are actually self-equilibrating within each individual constituent material within the RVE. Consequently, neither the composite average stress state (σc) nor the constituent average stress states (σf and σm) contain any measure of these self-equilibrating shear stresses.
While it is generally accepted that the actual micromechanical stress field σij(x,y,z) causes damage evolution and failure in the individual constituent materials and their material interfaces, the development of models that directly make use of the actual micromechanical stress field is an overwhelming, complex, and computationally intractable proposition. In Multicontinuum Theory, we focus instead on the concept of constituent average stress states, where the actual micro-structural stress field σij(x,y,z) is volume-averaged over each constituent material in the microstructure. However, to effectively utilize constituent average stress states in a structural-level analysis, it is critical to develop very efficient means of computing constituent average stress states. For practical reasons, structural level analysis of composite structures is formulated in terms of the composite average stress state. Therefore, the use of constituent average stress states requires a method to decompose a composite average stress state into constituent average stress states. This process, referred to as the MCT decomposition, will be described in the next section.