Convergence Issues for Progressive Failure Analyses

Address the common difficulty experienced with most progressive failure problems.

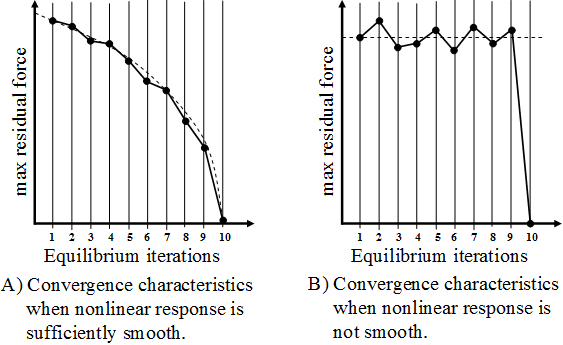
Most commercial finite element codes employ equation solvers based on the Newton-Raphson algorithm. The fundamental assumption implicit in the use of the Newton-Raphson algorithm is that the nonlinear response of the system is sufficiently smooth. Provided the nonlinear response of the system is indeed sufficiently smooth and that the Newton-Raphson algorithm is initiated with an approximate solution that is sufficiently close to the actual solution, the Newton-Raphson algorithm produces a sequence of solutions that exhibit quadratic convergence (qualitatively illustrated in Part A of the graphic below).

However, in a progressive failure analysis, the nonlinear response of the system is not smooth, especially at the local level where material failure results in large discontinuities in the material's constitutive behavior (e.g., see the graphic in the Damage States in Unidirectional Composite Materials section). This non-smooth response of the system completely changes the convergence characteristics of the nonlinear solution process. Part B of the graphic below qualitatively illustrates the type of convergence behavior that occurs in solving non-smooth systems such as those encountered in progressive failure analyses. The most significant characteristic observed in Part B is that the size of the largest residual force does not necessarily exhibit a continual decrease as equilibrium iterations are performed. In fact, the size of the largest residual force remains relatively constant, until suddenly the residual forces vanish indicating the solution has been found.

The default nonlinear solution strategy employed by most commercial finite element codes is based on the assumption that the system will exhibit the convergence characteristics depicted in Part A above. Specifically, commercial F.E. codes expect the size of the largest residual force to exhibit a continual and rapid decrease as equilibrium iterations are performed. In the event that residual forces do not appear to be decreasing significantly with each new equilibrium iteration, commercial F.E. codes assume the amount of nonlinearity present in the current time increment is too great. Consequently, commercial F.E. codes opt to decrease the size of the time increment in an attempt to limit the amount of nonlinearity present in the system's response. This philosophy is not appropriate for progressive failure analyses where the nonlinear response of the system is not smooth and the residual forces are not expected to exhibit a continual decrease. In fact, the application of this methodology to progressive failure analyses is counter-productive, resulting in the use of prohibitively small time increments that make completion of the analysis impractical.

Firehole Composites (now Autodesk) has developed proprietary algorithms that are implemented in Helius PFA to resolve the convergence difficulties normally associated with rapid degradation of material stiffness. When Helius PFA is used to provide material stiffness degradation, the finite element code exhibits robust convergence for progressive failure simulations. Based on considerable experience with progressive failure analyses, it is recommended that the finite element code should permit at least 50 equilibrium iterations to be performed before evaluating the need for a reduction in the size of the load increment.