Pre-Failure Nonlinearity (Nonlinear Longitudinal Shear Response)
Examine the effects of the nonlinear longitudinal shear response of composite materials.
Prior to ultimate failure, composites typically exhibit very little nonlinearity in the normal stress/strain response. However, they typically exhibit significant nonlinearity in the shear stress/strain response prior to ultimate failure. This nonlinearity is especially pronounced in the case of the longitudinal shear response (i.e.,  vs.
vs. 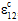 and
and 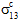 vs.
vs. 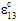 ).
).
It is assumed that the source of the composite material's nonlinear longitudinal shear behavior is the accumulation of sub-microcracks in the matrix constituent while the fiber constituent remains undamaged. It is further assumed that the accumulation of sub-microcracks in the matrix constituent leads to a progressive degradation of the longitudinal shear modulus of the matrix constituent and a corresponding progressive degradation of the longitudinal shear modulus of the composite material, without affecting any of the remaining composite or constituent moduli.
For situations where this nonlinear longitudinal shear behavior is important to you, Helius PFA provides a pre-failure nonlinearity feature that incorporates nonlinear longitudinal shear softening into the responses of both the matrix constituent and the composite material. For the sake of computational expediency and algorithmic simplicity, the degradation of the matrix average longitudinal shear moduli (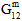 and
and 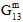 ) and composite average longitudinal shear moduli (
) and composite average longitudinal shear moduli (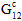 and
and 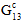 ) is not modeled as a continuous degradation. Rather, it is imposed via a series of discrete reductions that occur prior to the detection of matrix constituent failure (hence the name pre-failure nonlinearity). Three discrete reductions are applied to unidirectional composites and six discrete reductions are applied to woven composites. It should be emphasized that any discrete reduction in the matrix average longitudinal shear moduli (
) is not modeled as a continuous degradation. Rather, it is imposed via a series of discrete reductions that occur prior to the detection of matrix constituent failure (hence the name pre-failure nonlinearity). Three discrete reductions are applied to unidirectional composites and six discrete reductions are applied to woven composites. It should be emphasized that any discrete reduction in the matrix average longitudinal shear moduli (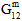 and
and 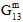 ) must be consistent (in the MCT sense) with the discrete reduction in the composite average longitudinal shear moduli (
) must be consistent (in the MCT sense) with the discrete reduction in the composite average longitudinal shear moduli (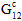 and
and 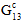 ) since the composite properties are obtained by homogenization of the heterogeneous microstructure.
) since the composite properties are obtained by homogenization of the heterogeneous microstructure.
To set the stage for describing the implementation of the pre-failure nonlinearity feature, refer to Part A of the plot in the Damage States in Unidirectional Composite Materials section. Focus on the initial linear elastic region (labeled Damage State 1) that occurs prior to any matrix or fiber constituent failure. As stated earlier, a linear elastic response prior to matrix failure is reasonable for normal stresses. However, the longitudinal shear stiffness of a composite material should exhibit a significant amount of softening prior to matrix failure.
Unidirectional Composites
Within the region labeled Damage State 1 in Part A of the plot mentioned above, the Helius PFA pre-failure nonlinearity feature employs a four-segment, piecewise linear representation of the longitudinal shear response (i.e.,  vs.
vs. 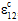 and
and 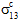 vs.
vs. 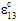 ). The original linear elastic response for the remaining four stress and strain components is maintained. The plot below provides a qualitative illustration of the composite average longitudinal shear response (
). The original linear elastic response for the remaining four stress and strain components is maintained. The plot below provides a qualitative illustration of the composite average longitudinal shear response ( vs.
vs. 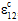 and
and 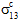 vs.
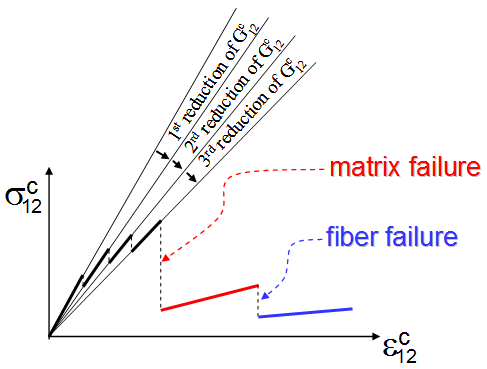
vs. 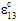 ) that occurs when the Helius PFA pre-failure nonlinearity feature is invoked for unidirectional composites. In this plot, prior to any matrix or fiber constituent failure, the composite average longitudinal shear moduli (
) that occurs when the Helius PFA pre-failure nonlinearity feature is invoked for unidirectional composites. In this plot, prior to any matrix or fiber constituent failure, the composite average longitudinal shear moduli (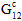 and
and 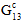 ) undergo a series of three discrete reductions. The discrete reductions in
) undergo a series of three discrete reductions. The discrete reductions in 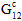 and
and 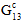 are produced entirely by consistent discrete reductions in the matrix average longitudinal shear moduli
are produced entirely by consistent discrete reductions in the matrix average longitudinal shear moduli 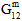 and
and 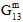 while all other matrix and fiber constituent properties remain constant. This procedure is intended to simulate the gradual accumulation of sub-microcracks in the matrix that occurs prior to complete matrix shear failure.
while all other matrix and fiber constituent properties remain constant. This procedure is intended to simulate the gradual accumulation of sub-microcracks in the matrix that occurs prior to complete matrix shear failure.
Woven Composites
Within the region labeled Damage State 1 in Part A of the plot mentioned above, the Helius PFA pre-failure nonlinearity feature employs a seven-segment, piecewise linear representation of the longitudinal shear response (i.e.,  vs.
vs. 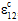 and
and 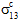 vs.
vs. 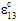 ). The original linear elastic response for the remaining four stress and strain components is maintained. The plot below provides a qualitative illustration of the composite average longitudinal shear response (
). The original linear elastic response for the remaining four stress and strain components is maintained. The plot below provides a qualitative illustration of the composite average longitudinal shear response ( vs.
vs. 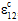 and
and 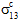 vs.
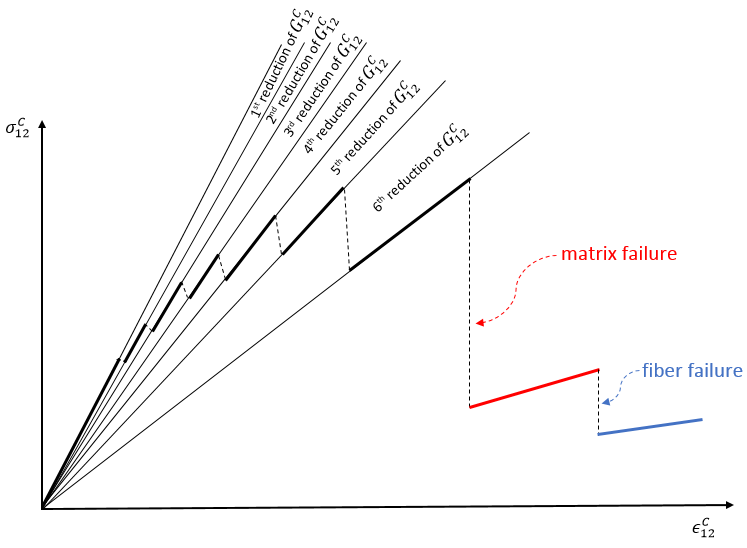
vs. 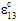 ) that occurs when the Helius PFA pre-failure nonlinearity feature is invoked for woven composites. In this plot, prior to any matrix or fiber constituent failure, the composite average longitudinal shear moduli (
) that occurs when the Helius PFA pre-failure nonlinearity feature is invoked for woven composites. In this plot, prior to any matrix or fiber constituent failure, the composite average longitudinal shear moduli (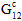 and
and 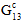 ) undergo a series of six discrete reductions. The discrete reductions in
) undergo a series of six discrete reductions. The discrete reductions in 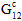 and
and 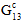 are produced entirely by consistent discrete reductions in the matrix average longitudinal shear moduli
are produced entirely by consistent discrete reductions in the matrix average longitudinal shear moduli 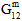 and
and 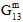 while all other matrix and fiber constituent properties remain constant. This procedure is intended to simulate the gradual accumulation of sub-microcracks in the matrix that occurs prior to complete matrix shear failure.
while all other matrix and fiber constituent properties remain constant. This procedure is intended to simulate the gradual accumulation of sub-microcracks in the matrix that occurs prior to complete matrix shear failure.
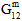 and
and 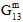 and the levels of matrix average longitudinal shear stress (
and the levels of matrix average longitudinal shear stress (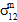 and
and 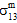 ) at which these reductions are imposed. Obviously, the determination of these constants requires a measured longitudinal shear stress/strain curve (e.g.,
) at which these reductions are imposed. Obviously, the determination of these constants requires a measured longitudinal shear stress/strain curve (e.g.,  vs.
vs. 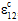 ) for the composite material in question. It should be emphasized that invoking this feature does not change the shear stress level at which matrix failure occurs. However, it does increase the amount of shear deformation that occurs prior to matrix failure.
) for the composite material in question. It should be emphasized that invoking this feature does not change the shear stress level at which matrix failure occurs. However, it does increase the amount of shear deformation that occurs prior to matrix failure.