The final piece of the composite fatigue puzzle is linking the rate of bond breaking with macroscopic failure of the composite.

Evolution of the Damage Parameter

As noted previously, Hansen and Baker-Jarvis [36] linked KTF with macroscopic damage by introducing a damage parameter n that represented the percentage of microcrack density relative to the microcrack density at failure. The damage variable, which represents the fraction of microcrack density required for fracture, is initially zero and unity at failure. In their formulation, they introduced a differential equation for the evolution of a damage variable n with time t, where the evolution of the damage variable is directly related to the bond rupture rate. This method successfully predicted the strength of polymers subjected to a wide range of stress rates.

A differential equation describing the evolution of n is used that is very similar to the one proposed by Hansen and Baker-Jarvis

n 0 is a parameter determined by enforcing the condition

and ni is the value of damage at the beginning of the fatigue loading. The distinction between this formulation and that of Hansen and Baker-Jarvis is that their formulation assumed λ=1. This value is the default value used in our current implementation 2 . For the case of λ=1,

Assuming a value of 1.0 for λ, and combining Eqs. 57, 52, and 56 gives the starting equation for determining the fatigue life of a polymer.

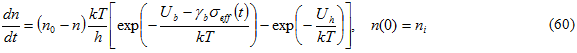
Solving Eq. 61 yields the evolution of the damage parameter with time, which can be written as 3 :

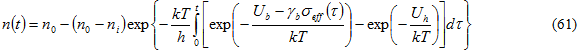
Eq. 61 can be used with calibrated values of Ub, 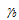, and Uh to determine the time at which the damage parameter becomes unity (n = 1).

2 For a single linear elastic analysis, i.e. no progressive failure, the choice of λ is irrelevant. All solutions of λ will yield the same number of cycles to failure. However, this factor could be critical for block loading and progressive failure simulation.

3 We have assumed the formulation in Eq. 61 assumes that U and T are constant during the fatigue process.