Determine the average matrix stress used to predict the bond breaking and bond healing rates.

Given a composite stress state or stress history, predict the bond breaking rate according to Eq. 40 and bond healing rate according to Eq. 41. One obvious challenge in this process is determining how to represent the matrix stress tensor as an effective scalar stress that can be used with the equations describing KTF. Several researchers have shown that an appropriate parameter for predicting fatigue life is the fatigue strength normalized by the static strength under the same load condition [23, 44-45]. This is often called the strength-life equal rank assumption. Thus, we use the functional form of static failure criteria for determining an effective fatigue stress.

Unidirectional Composites

Unidirectional composites exhibit two separate modes (or processes) of fatigue failure in the plane of the lamina: off-axis and on-axis. Each process must have its own activation energy and activation volume, as the physics of microcrack accumulation are different for the two types of cracking. In addition, the effective stress definitions will be different. In this section, we define the effective matrix stress for both off-axis and on-axis loading.

Off-axis

In considering the form of the failure criterion, it is useful to consider the off-axis failure modes observed in experiment. It has been widely reported that fatigue failure often occurs via cracking parallel to fibers [24, 46] for unidirectional composites. Thus, it is expected that tensile forces perpendicular to the fibers will play a substantial role in fatigue as well as the shear stresses on these planes. Taking the axial direction of the fiber to be the 1-direction, we propose an in situ matrix failure criterion in the form of transversely isotropic invariants of the matrix stress tensor calculated using MCT that takes the form

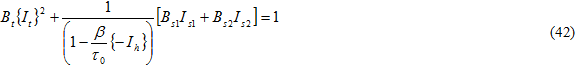
where

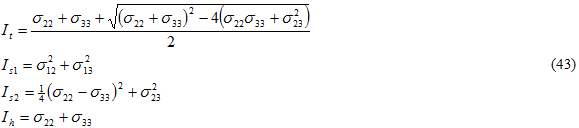
and the {} denote Macaulay brackets, such that the value is zero if the encompassed quantity is negative. The values of Bi are determined from three composite static failure tests: transverse tension, transverse compression, and in-plane shear. Each involves failure of the matrix constituent. Dividing Eq. 42 by Bs1 gives a form for an effective stress σ eff

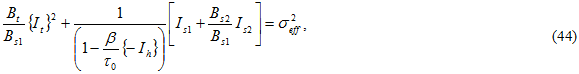
where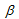 is a pressure strengthening coefficient and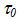is the matrix shear strength with no pressure strengthening. In the current version, all calculations use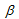= 0. Taking the square root of Eq. 44 gives the effective stress for computing the bond breaking rate according to Eq. 40 and 41.

On-axis

On-axis loading failure results from matrix cracks that arrest at the fiber/matrix interface. These cracks are primarily driven by normal stresses in the axial direction. Thus, for the case of on-axis failures (θ = 0°), the effective stress is defined as