Thermally Activated Processes
See how KTF is influenced by thermally activated processes.
All atoms and molecules at temperatures greater than absolute zero oscillate with a frequency proportional to n 0 given by Planck's Law,
where h is Planck's constant (h = 6.626068 × 10-34 J-s/K-atom) and kT is the thermal energy, described by the product of the Boltzmann constant k (k = 1.3806504 × 10-23 J/K-atom) and the absolute temperature T. But because the thermal energy associated with each oscillation is not really a single number but rather a distribution, there is always a chance any given oscillation will have sufficient energy to overcome the energy barrier U and move from one equilibrium state to another. The likelihood of this occurring for any given oscillation is given by the familiar exponential form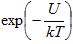 
. Thus, the bond breaking rate K b can be written simply as
For the purposes of fracture and fatigue, one equilibrium state is the unbroken state and the other is the broken state. The process is illustrated schematically in the left image below. Thus, a similar equation can be written for bond healing as
Now consider the effect of an applied stress on the bond breaking rate described in Equation (38) and the bond healing rate described in Equation (39). In this context it is more helpful to think of stress in terms of energy per unit volume rather than force per unit area. Thus, if the stress is acting to facilitate the bond-breaking process it should reduce the energy barrier to bond-breaking and increase the energy barrier required for bond healing.
The difference depends on the volume of material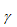 
, the activation volume over which the process occurs 1 so that the reduction in the activation energy is simply the product of activation volume and the stress. The image below on the right shows how the stress modifies the activation energy. Modifying Equation (38) to reflect the effect of an applied stress gives
Similarly for Eq. 39
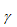are different for bond healing and bond breaking, as the activation energies and activation volumes are physically different for these two processes. Eqs. 40 and 41 are the baseline equations for the KTF that Helius PFA uses to predict composite fatigue.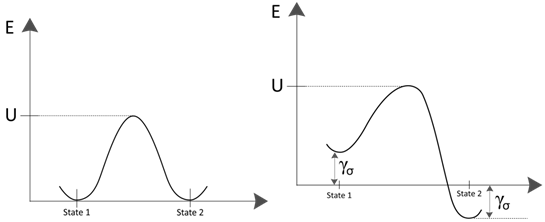
1 The precise definition of activation volume is somewhat ambiguous for the process of polymer fracture because it is much larger than, say, the atomic volume. Thus, it is typically only defined as the volume over which the activated process occurs.