Develop the relationships for a two-constituent (fiber/matrix) composite.

In a structural level analysis, we have direct access to the composite average stress and strain states (σc and εc) at any material point in the composite structure. In this section, we will develop the relationships for a two-constituent (fiber/matrix) composite that permit εc to be decomposed into the constituent average stress and strain states (σf, εf, σm, εm). The framework for this MCT decomposition will be provided by Equations 4 and 8 of the previous section, which are valid for any of material response and all levels of deformation.

The first step in the development of the MCT decomposition is to invoke suitable constitutive relations that express average stress measures in terms of the corresponding average strain measures. We impose the restriction that constitutive relations be linear so the MCT decomposition remains unique and mathematically tractable. We will see later, the restriction to linear constitutive relations does not pose a serious limitation; the MCT decomposition can still be utilized in nonlinear problems. Equations 12-14 list the various volume-averaged, linearized constitutive relations that will be employed.

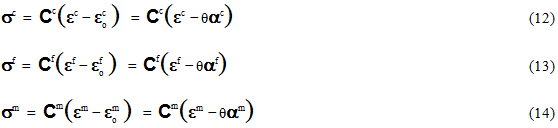
In Eqs. 12-14, Cc, Cf and Cm represent the 6x6 constitutive matrices (secant formulation) for the homogenized composite, the fiber constituent, and the matrix constituent materials respectively. θ represents a uniform temperature change of the composite material relative to the uniform reference temperature where material properties were measured. The terms αc, αf, and αm are 6x1 vectors that represent thermal coefficients of expansion for the homogenized composite, fiber constituent, and matrix constituent materials respectively. Since the constitutive relations are linear, the individual components of Cc, Cf, Cm, αc, αf, and αm are simply constants. However, to apply the MCT decomposition to nonlinear problems, it is assumed that the constitutive relations (Eqs. 12-14) are linearized about the current state (as defined by σc, εc, σf, εf, σm, εm and θ). This approach is entirely consistent with the approach commonly employed in nonlinear structural level analyses where an overall nonlinear response of a composite structure is represented by a sequence of piecewise linear responses.

Next, the linearized constitutive relations (Eqs. 12-14) are substituted into Eq. 4, yielding

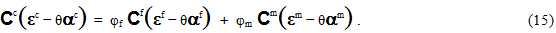
Further substituting Eq. 8 into Eq. 15 yields

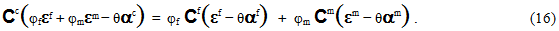
Eq. 16 can now be solved for the fiber average strain state (εf) by grouping similar terms and multiplying all terms by 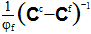, yielding

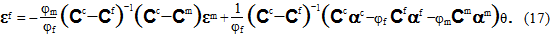
At this point, you can easily appreciate the restriction to linearized constitutive relations imposed earlier. Specifically, if the components of Cc, Cf, Cm, αc, αf, and αm are not constants, the algebra leading to Eq. 17 is intractable.

For convenience, let us now define a 6x6 matrix A and a 6x1 vector a as follows.

Using these newly defined quantities, Eq. 17 can be written simply as

Note that the matrix A relates the average mechanical strains in the constituents, while the vector a relates the average thermal strains in the constituents. Equation 19 can now be used to eliminate the average fiber strain εf from Eq. 8, yielding an expression for the matrix average strain state εm in terms of the composite average strain state εc.

Once the matrix average strain state εm is computed via Eq. 20, the fiber average strain state εf can be computed simply using Eq. 8, as

After having computed both the matrix and fiber average strain states (εm and εf), the matrix and fiber average stress states (σm and σf) can be computed using the linearized constitutive relations (Eqs. 13 and 14).

To summarize, the analytical form of the MCT decomposition is composed of four equations (Eqs. 20, 21, 13 and 14) used to decompose a composite average strain state at a material point into constituent average strain and stress states at the same material point. This decomposition can be performed very efficiently at any point within a composite structure where we know the composite average strain state. The MCT decomposition is an enabling technology that provides increased physical insight into the state of the heterogeneous composite microstructure. As we shall see later, the main benefit derived from knowledge of the constituent average stress and strain states is an improved physical basis from which to predict damage evolution and material failure within the constituent materials of the composite microstructure.

The foundation equation of the MCT decomposition is provided by Eq. 20 which can be thought of as a transfer function that maps a composite average strain state εc into the matrix average strain state εm. It is worthwhile to reiterate the implications of using Eq. 20 for a composite material that exhibits a nonlinear response. First, the mapping of εc into εm is completely defined by the quantities Cc, Cf, Cm, αc, αf, αm, φf and φm which are each assumed to be constant. Therefore, for non-linear material responses or finite deformations, the constitutive relations (Eqs. 12-14) must be linearized about the current material state (as defined by σc, εc, σf, εf, σm, εm, and θ). The implication of this restriction is that the overall nonlinear response of the composite material must be represented by a finite sequence of linear responses where Cc, Cf, Cm, αc, αf, and αm can be considered constant within each segment of the response. In practice, the MCT decomposition is different for each segment of the response since Cc, Cf, Cm, αc, αf, and αm change from one segment to the next. Again, this piecewise linear representation of the material response is entirely consistent with the method commonly used in performing nonlinear structural level analyses.

It should also be emphasized that the MCT decomposition (collectively Eqs. 20, 21, 13, 14) requires a minimal amount of computational work. Therefore, it can be applied to all points of interest in a structural level analysis without significantly increasing the total computational time. For example, in a structural level finite element analysis of a composite structure, use of the MCT decomposition at each Gaussian integration point in the model typically only increases the total solution time by 2%-3%.

The analytical binary decomposition is particularly advantageous for simple, unidirectional fiber-reinforced composite materials. Helius PFA uses the analytical binary decomposition for all unidirectional reinforced composite materials. Even for woven or braided composites, the final decomposition from tow average stress and strain to fiber and matrix average stress and strain is performed using the analytical binary decomposition.