Once damage initiates in a cohesive material the stiffness of the material begins to reduce (damage evolves). Damage will continue to evolve as the deformation of the material continues to increase. Eventually the material will be considered fully damaged and contain zero stiffness. The reduced material stiffness is controlled by the damage variable, D, which is given as:

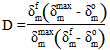
where 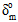is the effective relative displacement at damage initiation, 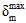is the maximum effective relative displacement attained thus far in the loading history, and 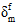is the effective relative displacement at complete failure. Effective displacement is defined as:

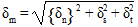
where δn, δs, and δt are the three relative displacements in the local three, one, and two directions, respectively. The traction is then calculated using the original stiffness values and the damage variable as shown:

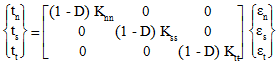
A typical traction displacement curve is shown below. Damage initiates at 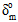where D=0, and then damage continues to evolve to the point where D=1 at .

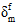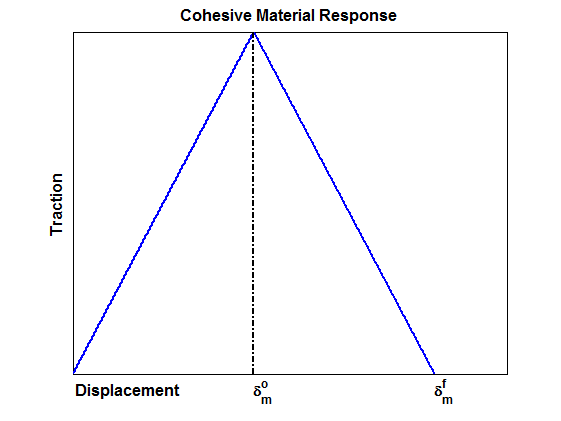
Displacement Based Damage Evolution

For the displacement based damage evolution criterion, argument 10 is interpreted as the difference between the effective relative displacement at complete failure, 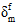, and the effective relative displacement at damage initiation, 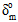. Valid values must be greater than zero. The image above shows qualitatively how 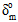and 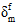relate to the rate of damage evolution.

Energy Based Damage Evolution

For the energy based damage evolution criterion, argument 10 is interpreted as the total fracture energy of the cohesive material, GC. The image below shows how GC relates to the traction-separation response of the cohesive material. The value of GC you supply is used to determine the final relative effective displacement as:

where 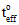is the effective traction at damage initiation.

Energy Based Damage Evolution (Mixed Mode, Power Law)

The energy based mixed mode power law criterion uses fracture energies for each loading mode to determine damage evolution. Instead of a single fracture energy, GC, you supply the fracture energy for each mode ( 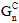, , 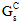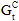) via arguments 10, 11, and 12 respectively. You must also supply an exponent, α, to be used in the power law. The power law states when the following condition is met the cohesive material has completely failed (D = 1):

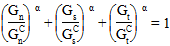
where Gn, Gs, and Gt are the work done by the traction and the corresponding relative displacement in the local three, one, and two directions respectively.