Tolerance Calculation Formulas

Tip: For your 1D tolerance analysis calculations, consider using the Autodesk® Inventor® Tolerance Analysis add-in. Inventor Tolerance Analysis provides a rich set of tools that helps you more clearly understand the impact of mechanical fit and performance based on the cumulative dimensional variation.

For more information, see To Define Tolerance Stackups.

Derive basic equations for closed linear dimension chains from the following image.

a = 32 ± 1.5 mm, b = 8 ± 1 mm

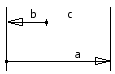
Increasing/decreasing elements

If the increasing element increases, the closing element also increases. If the decreasing element increases, the closing element decreases, if other elements of the chain remain constant.

Closing element:	1. c = a - b
Upper limit dimension of the closing element:	2. c max = a max - b min
Lower limit dimension of the closing element:	3. c min = a min - b max
Tolerance of the closing element (subtracting equation 3 from equation 2)	4. c max - c min = a max - a min - (b min - b max )
Such as	5. T c = T a + T b

Note: The tolerance of the closing element equals a sum of tolerances of all closed dimension chain elements

In general, linear chain tolerances satisfy the following equation.

Similarly, equations 2 and 3 can be written in a general form.

Upper limit dimension of the closing element equals a difference of the sum of upper limit dimensions of increasing elements and the sum of lower limit dimensions of decreasing elements.

Lower limit dimension of the closing element equals a difference of the sum of lower limit dimensions of increasing elements and the sum of upper limit dimensions of decreasing elements.

Nominal dimension of the closing element can be expressed using equation 1, as in the following equation.

Upper limit deviation of the closing element.

Lower limit deviation of the closing element.