The 3D flow results are based on the following considerations.

To simulate the flow inside the mold cavity, the conservation equations of momentum, mass and energy are discretized into finite elements.

This is defined by the following equations:

Conservation of mass for a fluid

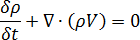
Where

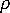• is the polymer density
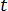• is time
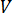• is the velocity vector

Conservation of momentum

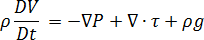
Where

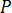• is pressure
• is the viscous stress tensor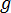
• is the gravitational acceleration vector

Conservation of energy

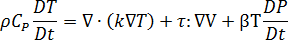
Where

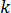• is the polymer thermal conductivity
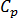• is the specific heat capacity of the melt
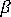• is the polymer expansivity which is defined as follows

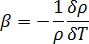
For the Pressure-velocity solution

• The equations are solved by a standard finite element method. This includes the material compressibility in all process stages.
• The beam and tetrahedral elements are solved simultaneously.
• All the tetrahedral nodes in the shadow of each beam element are tied to the same pressure.
• In beam elements, a 1D flow is assumed and a Hele-Shaw approximation is used.
• In tetrahedral elements, a full Stokes solution is performed (or Navier-Stokes if the inertia option is selected) .

For the Temperature (energy conservation) solution

• Equations are solved by a standard finite element method.
• For both beam and tetrahedral elements, we include the shear heating, convection, conduction and compressive heating terms.
• In the beam elements, we approximate negligible conduction along the beam length. For temperature convection in beam elements, we upwind within each beam laminate.
• When solving the temperature equations, we break the time-step into a number of shorter sub-steps for increased accuracy.

At each time-step, we iterate between the temperature and pressure-velocity equations until convergence is reached.