Calcula tornillos de potencia con carga de torsión y de presión, y realiza una comprobación de deformación y presión en la rosca en unidades métricas o imperiales, según la norma especificada. Si se selecciona la norma ANSI, se utilizan unidades imperiales con las cotas de tornillo correspondientes.
Parámetros de entrada
|
F |
fuerza axial máxima [N, lb] |
|
T |
momento máximo [Nm, lb pies] |
|
f 1 |
coeficiente de fricción de rosca entre la tuerca y el tornillo [-] Nota: La influencia del ángulo de la rosca se debe incluir en el valor del coeficiente de fricción de rosca.
|
|
d |
diámetro de la rosca del tornillo [mm, pulg] |
|
p |
separación [mm, pulg] |
|
d s |
diámetro medio del tornillo [mm, pulg] |
|
d min |
diámetro mínimo del tornillo [mm, pulg] |
|
H |
altura de la tuerca [mm, pulg] |
|
n |
factor para condiciones finales según la imagen esquemática de los tipos de montaje [-] |
|
L |
longitud máxima del tornillo con carga [mm, pulg] |
|
S y |
límite de elasticidad [MPa, lpc] |
|
k s |
coeficiente de seguridad (El valor se selecciona según el nivel de seguridad necesario.) [-] |
|
p a |
presión de rosca admitida [MPa, lpc] |
|
E |
módulo de elasticidad del tornillo [MPa, lpc] |
Parámetros calculados
Longitud reducida
L red = n L
Sección de área mínima
S min = π d min 2 / 4
Ángulo de hélice (ángulo de avance)
![]()
Eficiencia
Para “rotación a desplazamiento”
|
|
Para “desplazamiento a rotación”
|
|
|
|
Si α < arc tan f 1 , η = 0 |
Momento máximo (si se trata del momento de salida)
T = F p / (2 πη)
Fuerza axial máxima (si se trata de la fuerza de salida)
F = 2 T πη / p
Coeficiente de esbeltez
λ = 4 L red / d s
Tensión de presión
σ t = F / S min
Tensión de torsión
![]()
Tensión reducida
![]()
Tensión crítica de Rankin
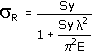
Tensión crítica de Euler
σ E = π 2 E / λ 2
Tensión crítica de Johnson
![]()
Presión calculada en la rosca

Coeficiente de seguridad calculado
k v = min (S y / σred, min (σ R , σ F , σ J ) / σ t )
Comprobación de resistencia
k v ≥ k s
p c ≤ p A