Base teórica de los métodos utilizados durante el análisis dinámico de la estructura

Introducción

En este documento, se describen los métodos de análisis dinámicos aplicados en Robot. Los antecedentes teóricos y los ejemplos se incluyen en los apéndices. Esta sección no se basa en instrucciones y no tiene por objeto detallar la interfaz de Robot. Explica las principales ideas de este programa.

La mayoría de los métodos dinámicos de Robot se basan en los resultados del análisis modal. Es necesario comprender que los métodos de análisis modal dependen del tipo seleccionado de solvente. Para el solvente Skyline, están disponibles los siguientes métodos: iteración en el subespacio por bloques (BLSI), iteración en el subespacio (SI), Lanczos y reducción de la base. Entre los métodos disponibles para el solvente Sparse Direct, se incluyen: iteración en el subespacio por bloques (BLSI), Lanczos y reducción de la base. Mientras que para el solvente iterativo están disponibles los siguientes métodos: Lanczos modificado (pseudomodo, consulte la sección 3.5 y los anexos 3A y 3B), gradiente Ritz (PCG_Ritz) y gradiente conjugado preacondicionado (PCG).

El solvente Sparse Direct (SPDS) es una forma específica de eliminación de Gauss. Se recomienda encarecidamente para el análisis de problemas de tamaño medio y grande (10 000 - 200 000 ecuaciones) y es una excelente alternativa para el solvente iterativo.

3.1. Métodos de análisis modal

El análisis modal se compone de dos enfoques básicos. El análisis de problemas con valores propios

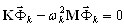k = 1,2,…,N (3.1)

se genera mediante la definición de los valores propios wk y los vectores propios 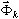. Es el primer enfoque que le resulta familiar a los ingenieros. El segundo enfoque se compone de la generación de vectores base

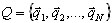(3.2)

y la búsqueda de aproximaciones de Ritz , (k=1,2,..., N). Se basa en el método de vectores de Ritz dependientes de la carga, propuesto por E.L. Wilson [1, 3] y aplicado en SAP2000. Este enfoque se aplica para el análisis sísmico y es un método eficaz cuando hay grandes dificultades para obtener un porcentaje de masa suficiente (consulte la sección 3.5).

Cuando se seleccionan solventes directos (Skyline o SPDS), se utilizan la iteración en el subespacio por bloques (BLSI), la iteración en el subespacio (SI), la ortogonalización selectiva de Lanczos y la reducción de la base (consulte el apéndice 3A). El método de iteración en el subespacio suele ser lento. Por lo tanto, se recomienda encarecidamente la aplicación de BLSI o Lanczos para el análisis de problemas de tamaño medio y especialmente a gran escala cuando se requiere un gran número de pares propios. La reducción de la base puede resultar muy eficaz para un ingeniero experimentado. Sin embargo, requiere información adicional sobre los nudos base y las direcciones base adecuadas.

Gradiente conjugado preacondicionado (PCG)

Este método se utiliza en el primer enfoque, cuando se selecciona un solvente iterativo. Este enfoque puede ser muy eficiente cuando se extraen pequeños números de modos propios (como máximo 5). Debe utilizarse para el análisis de viento en lugar de para el análisis sísmico. El método PCG permite calcular el modo propio más bajo cuando se da un problema a gran escala.

El segundo enfoque (que se aplica mediante el análisis de pseudomodo) se describe en la sección 3.5.

Iteración en el subespacio por bloques (BLSI)

Este método [1,3] es más general que el de Lanczos, ya que permite la implementación de todos los tipos de matrices de masas (consulte la sección 3.2) y es capaz de analizar estructuras independientes. Las iteraciones en un bloque del tamaño constante con la exclusión inmediata de vectores convergentes y la adición de nuevos vectores iniciales normalmente garantizan cálculos más rápidos en comparación con el método habitual de iteración en el subespacio [1-3]. Al igual que en el método de Lanczos, se puede aplicar BLSI para extraer un gran número de pares propios (hasta 100 - 200).

Iteración en el subespacio (SI)

Este método se puede utilizar para el análisis de todos los tipos de matriz de masas [4] y de estructuras independientes. No obstante, en el caso de un gran número de modos necesarios (aproximadamente N > 10), este método sigue siendo muy lento, sobre todo, en problemas a gran escala.

El método de Lanczos [12,16,17] es un método eficaz que permite obtener un gran número de pares propios (N ~ 20 - 500 y más). Aunque es preferible para problemas a gran escala, presenta las siguientes limitaciones:

• Es imposible analizar estructuras independientes.
• La matriz de masas debe ser de tipo concentrada con rotaciones o coherente.
• Es imposible ignorar la densidad del material (en este caso, basta con asignar una pequeña densidad ficticia para evitar estas limitaciones).

Reducción de la base

Este método [5] se conoce por el nombre de los métodos mejorados Rayleigh-Ritz [4] o Bubnov-Galerkin para sistemas discretos. Este algoritmo permite obtener valores aproximados de los primeros pares propios si se conoce alguna información sobre ellos. Para este método, es necesario aplicar un grado principal de libertad (MDOF) para obtener el sistema reducido. De este modo, se puede controlar el proceso de creación del modelo reducido. Es una herramienta muy eficaz para quienes tienen experiencia en el análisis dinámico de estructuras y se ocupan de un tipo de estructuras similar con un comportamiento conocido. Este método permite excluir grados de libertad (DOF) no deseados del modelo reducido y rebaja el problema complejo inicial con un gran número de grados de libertad a una forma reducida. Esto se consigue con un número considerablemente menor de grados de libertad. La experiencia relativa al análisis dinámico de la estructura muestra que el usuario puede encontrar algunos problemas cuando los métodos de reducción automática (se tienen en cuenta BLSI, SI y Lanczos) dan lugar a un proceso de cálculo muy complejo. Por ejemplo, los modos de vibración local de las barras individuales pueden provocar problemas graves, ya que el proceso de cálculo busca automáticamente los pares propios sin ninguna selección. Esto se debe tener en cuenta en estructuras de carácter real en la mayoría de los casos. De lo contrario, estas vibraciones locales quedarán restringidas por algunas limitaciones ignoradas en el modelo MEF o aportarán poco al movimiento general del sistema. Normalmente, el porcentaje de masa es muy pequeño para estas vibraciones locales. El uso de métodos exactos en este caso dará lugar a las dificultades mencionadas anteriormente. Sin embargo, la implementación del método de reducción de la base aproximada puede simplificar considerablemente el proceso de cálculo.

Gradiente conjugado preacondicionado (PCG)

Este método [9-13] está disponible para los solventes iterativos. Se recomienda aplicar este método para extraer un número reducido de pares propios cuando se resuelva un problema a gran escala. Es recomendable aplicar el pseudomodo (consulte la sección 3.5) con PCG_Ritz o Lanczos modificado si es necesario determinar un gran número de modos mientras se ejecuta el análisis sísmico o espectral y se selecciona un solvente iterativo.

Gradiente Ritz (PCG_Ritz)

Este método [8] está disponible para los solventes iterativos en el pseudomodo. Permite producir una solución aproximada en términos de vectores de Ritz. Es un método muy rápido para el análisis sísmico y espectral de tamaño medio (10 000 - 100 000 ecuaciones).

Lanczos modificado

Este método es una extensión del método de Lanczos cuando se aplica un solvente iterativo. Actúa como el método de Lanczos en el pseudomodo. Sin embargo, al ser diferente a Lanczos para los solventes directos, no requiere una factorización de una matriz de rigidez. En su lugar, se aplican los principios del método de gradiente preacondicionado. Este enfoque es el más sólido entre todos los métodos dinámicos de los solventes iterativos, aunque a menudo no parece ser el más rápido.

En el apéndice 3A, se ofrece información de todos los métodos dinámicos.

3.2. Tipos de matriz de masas

Las matrices de masas concentradas sin rotaciones, concentradas con rotaciones y coherentes de los análisis dinámicos se pueden aplicar a una estructura.

Las matrices concentradas sin rotaciones y concentradas con rotaciones son tipos de matrices de masas diagonales. Estos tipos de matrices de masas requieren un esfuerzo de cálculo mínimo.

La matriz de masas coherente aparece cuando se tiene en cuenta un sistema con parámetros distribuidos. Se suele creer que una matriz de masas coherente describe las propiedades de inercia de una estructura con más exactitud que una concentrada. Sin embargo, en la mayoría de los casos, una matriz de masas concentrada proporciona una buena aproximación, ya que es obvio que los parámetros de inercia se pueden presentar con menor precisión que la rigidez. De hecho, la energía cinética se describe como desplazamientos de una estructura, pero la energía potencial se expresa mediante la derivada espacial de los desplazamientos. Es un hecho bien conocido que el error de aproximación aumenta considerablemente durante cada diferenciación [4]. Por lo tanto, en el caso de objetos continuos (sólidos, láminas y pletinas), es posible aproximar los parámetros de masa con una precisión menor que la rigidez de la misma malla.

Por lo general, los polinómicos Hermit se utilizan como funciones de forma para barras. Es una solución exacta para la mayoría de los problemas estáticos y dinámicos cuando se tiene en cuenta la matriz de masas concentrada. Sin embargo, las soluciones exactas para los problemas dinámicos de una barra con masas distribuidas pertenecen a la clase de funciones Krylov (una combinación específica de funciones hiperbólicas y trigonométricas). Permite presentar los parámetros de rigidez de forma aproximada cuando se utilizan polinómicos Hermit simultáneamente con una matriz de masas coherente. No se ha diseñado para implementar un tipo diferente de función de forma para problemas estáticos y dinámicos. Por lo tanto, en la mayoría de los casos, no es beneficioso complicar el modelo dinámico mediante el uso de parámetros de masas distribuidas, ya que se ofrece la solución aproximada con masas coherentes en lugar de la solución exacta para un modelo aproximado (masas concentradas).

Además, por lo general, las masas de elementos estructurales de barras (jácenas, pilares, etc.) son insignificantes en comparación con las masas de muros y tejados (peso propio), que se tienen en cuenta mediante la conversión de pesos propios en masas. Estas masas no estructurales suelen reducir los efectos de las masas de elementos distribuidos.

En la mayoría de los casos prácticos, la matriz de masas concentrada garantiza una aproximación suficientemente precisa de las propiedades de inercia de la estructura. Se debe recordar que una matriz de masas coherente requiere esfuerzos de cálculo considerables si se analiza un problema a gran escala. La implementación de una matriz de masas coherente debe justificarse antes de seleccionar este tipo de matriz para el análisis.

Se presupone que la matriz de masas debe ser coherente si se utilizan uniones rígidas en el modelo de cálculo.

Si se aplica un solvente Sparse Direct o uno iterativo, se utiliza la técnica de elemento por elemento (EBE) para el cálculo de un producto de vector de matriz. La matriz de masas coherente nunca se puede ensamblar. Sin embargo, todas las operaciones se realizan solo en el nivel de elemento. En el caso del solvente Skyline, se ensambla y se almacena una matriz de masa coherente de la misma forma que una matriz de rigidez. Para problemas pequeños (~3000 ecuaciones como máximo), la técnica Skyline es más rápida, aunque aún requiere mucho tiempo cuando aumenta el tamaño de un problema.

Se pueden utilizar masas añadidas y convertir cargas estáticas en masas.

Cuando se seleccionan los métodos de Lanczos, PCG_Ritz o Lanczos (solvente iterativo) modificado, solo están disponibles las matrices de masas concentradas con rotación y coherentes.

3.3. Límites máximos

Se pueden calcular todos los valores y los modos propios que no superen un valor definido por el usuario. Este valor se considera como el "límite máximo". Si está activado, Robot busca ω₁, ω₂, …, ω_n ≤ ω^*, donde ω^* es el límite máximo. El algoritmo funciona en dos pasos. La verificación de secuencia Sturm se realiza en el primer paso, lo que define el número de valores propios n, que es el valor inferior del límite máximo. En el siguiente paso, el algoritmo genera n pares propios, cada uno más pequeño que el límite máximo.

Es recomendable utilizar los métodos BLSI y de Lanczos para el tipo de análisis que utiliza límites máximos, ya que es necesario obtener un gran número de pares propios.

El criterio del porcentaje de participación de masas (consulte la sección 3.4) se omite cuando se activa el límite máximo.

Por ejemplo, pueden surgir problemas al utilizar la norma sísmica francesa PS-92, ya que es necesario tener en cuenta todas las frecuencias inferiores a 33 Hz.

3.4. Porcentaje de participación de masas

La masa efectiva de cada modo (k=1,2,...,N) se define como

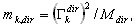
donde 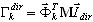, 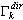es el coeficiente de participación de masas para el modo propio k, I_dir es el vector de conversión de unidades en la dirección (dir = X,Y,Z), 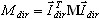es la masa total en dirección dir, 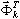es el modo propio en la posición k, .

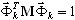La masa efectiva para la dirección dir es igual a M%dir 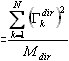. Define la contribución de todos los modos relacionados con el movimiento de una estructura en la dirección que se ha tenido en cuenta.

Si se selecciona Análisis modal y la masa efectiva de un número máximo especificado de nudos es inferior al necesario, una solicitud advierte de la masa efectiva insatisfactoria mientras los cálculos se siguen realizando sin ninguna corrección.

Es necesario definir el análisis del modo Sísmico o el pseudomodo para garantizar la búsqueda automática de la masa efectiva necesaria. Se proporciona información en la sección 3.5.

3.5. Modos de análisis

En esta sección, se presentan los modos de análisis dinámico (regímenes) Modal, Sísmico y pseudomodo.

Varias normas sísmicas (UBC-97 o la norma francesa PS-92) requieren que la suma de las masas de cada dirección (o solo para las direcciones horizontales) sea inferior al 90 %. Pueden surgir problemas al obtener la suma necesaria de masas debido a las pequeñas contribuciones de un gran número de los modos inferiores. Por lo general, esto se debe al carácter local de los modos inferiores. El modo Sísmico y el pseudomodo se ofrecen para mejorar la situación de problemas tan difíciles. La eficacia de estos métodos se muestra en el apéndice 3C. Lanczos para solventes directos está disponible para estos dos modos. Los métodos de Lanczos modificado y PCG_Ritz están disponibles para el pseudomodo cuando se selecciona el solvente iterativo.

Modal

Este modo constituye un enfoque conocido implementado en las versiones anteriores de Robot.

Están disponibles los métodos BLSI, SI, de Lanczos y de reducción de la base para solventes directos y el método PCG para solventes iterativos.

A continuación, se indican los criterios de convergencia de los solventes directos. Las iteraciones se detendrán cuando 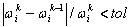, donde i = 1, 2, ..., N; k es el número de iteración y N es el número de modos (definido por el usuario). El método de reducción de la base no genera la comprobación de convergencia, ya que no es el enfoque iterativo, aunque sea un tipo de método Ritz. Es necesario aumentar el número de grados de libertad principales para mejorar la precisión de los resultados.

Entre los criterios de convergencia para el método PCG (solvente iterativo), se incluyen los siguientes:

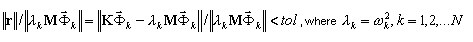
Los detalles se describen en el apéndice 3A.

Los límites máximos hacen referencia al valor de límite inferior para el periodo, la frecuencia y la pulsación. Si este parámetro es diferente a 0, se calcularán todos los pares propios secuenciales de 0 al límite máximo.

El valor de Mass% es la masa efectiva (suma de las masas de todos los modos calculados para cada dirección).

La verificación de Sturm es una comprobación de los pares propios omitidos entre 0 y el parámetro de desplazamiento y consiste en contar los elementos negativos en la diagonal de la matriz descompuesta desplazada .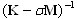

Es un procedimiento muy costoso para los problemas a gran escala. Tengamos en cuenta que, para el análisis sísmico y espectral, es innecesario obtener los espectros continuos de los valores propios. Solo es importante garantizar la masa efectiva modal suficiente para cada dirección. Si se cumple esa condición, se garantiza la integridad de la base. La implementación de BLSI permite producir la verificación parcial de la continuidad de los espectros de valores propios sin realizar la verificación de Sturm. Para obtener más información, consulte la descripción del método BLSI.

Número de modos	Límites máximos	Masa efectiva	Comportamiento del programa
N	0 (inactivos)	0 (inactivos)	La verificación de Sturm está activada.Faltan frecuencias omitidas para los primeros N modos. Está disponible para solventes directos cuando se aplican los métodos BLSI, SI o de Lanczos. No está disponible para el método de reducción de la base ni para todos los métodos de solventes iterativos. Defina N primeros modos propios secuenciales. Se realiza la verificación de Sturm. Si se detectan frecuencias omitidas, una advertencia solicita el número de ellas. Si se indica: Sí, el proceso de iteración continúa mientras se determina el número de pares propios omitidos. Después, se repite la verificación de Sturm. No, los pares propios convergentes se guardan como resultado final y se calcula el siguiente caso. Cancelar, las iteraciones continúan mientras se determinan todas las frecuencias omitidas. Se omite la advertencia. La verificación de Sturm está desactivada. No se realiza la verificación de Sturm.
N	ω *	Inactiva (debido al límite máximo activo)	Disponible solo para los solventes directos y los métodos BLSI, SI y de Lanczos. No está disponible para el método de reducción de la base ni para todos los métodos de solventes iterativos. La verificación de Sturm se realiza al inicio de los cálculos y se obtiene el número de frecuencias N1 que se encuentran entre cero y el límite máximo: 0 < ω1 < ω2 < … < ωN1 < ω* Si (N1 > N), una advertencia avisa del número de frecuencias N1. Si se indica: Sí, se calcula 0 < ω1 < ω2 < … < ωN1 < ω*. No, se detienen los cálculos. Si (N1 <= N), calcula 0 < ω1 < ω2 < … < ωN1 < ω* sin ninguna advertencia. En ambos casos, es posible derivar un número de pares propios convergentes superior a N1, pero solo se guardarán como resultados finales en el siguiente caso: 0 < ω1 < ω2 < … < ωN1 < ω*. Se perderán todos los pares propios convergentes que sean superiores a ω*.
N	Inactivos (debido a la masa efectiva activa)	Activa: 0< mass%<=100 %	Disponible para todos los métodos de solventes directos. No está disponible para el solvente iterativo. Si el valor de masa efectiva (mass%) no es satisfactorio, se emite la solicitud pertinente. No se realizan correcciones. De lo contrario, los cálculos se realizan de la misma forma que en el primer caso.

Sísmico

Este modo solo está disponible para los solventes Skyline o Sparse Direct.

En el análisis sísmico y espectral, no es importante utilizar valores propios ordenados secuencialmente, ya que solo deben tenerse en cuenta las valores propios que contribuyen considerablemente a la respuesta sísmica (ya que tienen un coeficiente de participación de masas significativo). Por lo tanto, no se realiza la verificación de Sturm.

El método de Lanczos suele garantizar la convergencia del número de pares propios considerablemente mayor que N pares propios en el orden secuencialmente creciente. Cuando es necesario restablecer los valores propios omitidos, se debe obtener el número de frecuencias convergentes considerablemente mayor que las primeras N frecuencias deseadas. Por ejemplo, es habitual que el método de Lanczos genere las siguientes frecuencias convergentes.

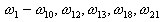
Cuando el usuario necesite los pares propios ordenados secuencialmente, obtendrá solo los 10 primeros. Los últimos cuatro valores propios simplemente se descartan, así como la contribución de masa de correspondencia. La esencia del modo "sísmico" propuesto es tener en cuenta todos los pares propios convergentes (no solo los primeros secuenciales). Esto garantiza una mayor suma de masas en comparación con el modo "Modal".

Métodos disponibles: método de Lanczos.

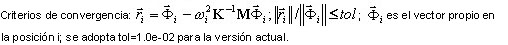
Se omiten los límites máximos.

La masa efectiva actual es el valor medio de M%x, M%y, M%z para problemas 3D y valor mínimo de M%x, M%z para los problemas 2D (M%x, M%y, M%z hacen referencia a la suma actual de las masas de las direcciones x, y, z respectivamente). Esta estrategia se explica por el hecho de que suele ser muy difícil garantizar una masa efectiva suficiente para la dirección vertical. Puede comprobar la masa efectiva de cada dirección en los resultados finales.

N modos	Límites máximos	Masa efectiva	Comportamiento del programa
N	Inactivos	Inactiva (0)	Calcule los N pares propios sin secuencia. No se realiza la verificación de Sturm. El número de pares propios convergentes es igual a N.
N	Inactivos	Activa: 0< mass%<= 100 %	No omite N. Los cálculos continuarán hasta que la masa efectiva actual no sea inferior a la masa efectiva demandada o se solicita al usuario que detenga los cálculos, o bien el número de pares propios convergentes alcanza el valor máximo disponible. Este conjunto de valores se define internamente y es 100 en la versión actual. Tras cada 20 pasos de Lanczos, el número de pares propios convergentes se vuelve a calcular y se modifica la masa efectiva actual. Una advertencia solicita la masa efectiva alcanzada. Si se indica: Sí, continúe con los cálculos durante los 20 pasos siguientes de Lanczos y vuelva a visualizar este mensaje. Si no se alcanza la masa efectiva necesaria (el número de pares propios convergentes no supera el valor máximo disponible). No, guarde los pares propios convergentes como resultados finales y páselos al siguiente caso. Cancelar, se omitirán todas las advertencias y se continuará con los cálculos.

Pseudomodo

Este modo está disponible para los solventes directos e iterativos. Se recomienda solo el análisis sísmico y espectral cuando los modos Modal y Sísmico consumen demasiado tiempo. Los modos Modal y Sísmico utilizan los modos propios como vectores base para presentar la respuesta sísmica y puede ser necesario un número muy grande de modos propios para garantizar una suma de masas suficiente para algunos problemas difíciles. El pseudomodo rechaza esta idea y genera las aproximaciones de Ritz a los pares propios más bajos mediante vectores de Lanczos para los solventes directos o los métodos de gradiente Ritz [8] y Lanczos modificado para los solventes iterativos. Esta es una forma de operar más efectiva en la mayoría de los casos porque se requiere un número menor de vectores base que en Modal. Esto fue demostrado por E.L.Wilson [1-3]. El pseudomodo es similar al de los vectores de Ritz dependientes, propuesto en [1-3] y aplicado en SAP2000. Cabe señalar que la norma francesa PS-92 admite la aplicación de enfoques científicos para añadir sistemas de vectores base a los modos propios existentes a fin de aumentar la suma de las masas. Puede encontrar información sobre el pseudomodo y su eficacia en los apéndices 3B y 3C, respectivamente.

Se omiten los límites máximos.

La masa efectiva actual se define como el valor medio de M%x, M%y, M%z para problemas 3D y valor mínimo de M%x, M%z para los problemas 2D (M%x, M%y, M%z hacen referencia a la suma actual de las masas de las direcciones x, y, z respectivamente). Esta estrategia se explica por el hecho de que suele ser muy difícil garantizar una masa efectiva suficiente para la dirección vertical. Puede comprobar la masa efectiva de cada dirección en los resultados finales.

N modos	Límites máximos	Masa efectiva	Comportamiento del programa
N	Inactivos	Inactiva (0)	Disponible para los solventes directos e iterativos. Genere N vectores base para definir el subespacio de trabajo. Guarde N vectores base para su uso con análisis sísmicos y espectrales. Se recomienda este régimen.
N	Inactivos	Activa: 0< mass%<= 100 %	Disponible solo para los solventes directos. Genere N vectores base para definir el subespacio de trabajo. Guarde estos vectores base, que serán suficientes para satisfacer la masa efectiva especificada. El número de vectores base guardados es inferior a N, si la masa efectiva es inferior al 100 %.

3.6. Análisis espectral

El método de espectros de respuesta se aplica para el análisis sísmico y espectral. Este método consiste en descomponer una estructura de varios grados de libertad (MDOF) en un sistema de osciladores de un solo grado de libertad (SDOF). La respuesta de cada uno de estos osciladores independientes y la suma estadística de las respuestas extremas de cada oscilador se calcula mediante los métodos SRSS, CQC, diez por ciento y doble suma [3, 21].

Los modos propios definen este sistema de osciladores SDOF cuando se aplican los modos Modal o Sísmico. Los vectores base del pseudomodo definen este sistema de osciladores SDOF cuando se aplica este modo (consulte la sección 3.5).

La introducción del pseudomodo requiere un nuevo enfoque en la evaluación de la respuesta para cada modo. El enfoque clásico es el siguiente:

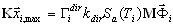( 3.1.1 )

donde K, M hace referencia a las matrices de masas y rigidez; Γ hace referencia al factor de participación de masas; S_a hace referencia a la aceleración de espectros; T indica el periodo, i hace referencia al número de modo, k es el coeficiente de escala del espectro, dir hace referencia al índice de movimiento sísmico de entrada (dir = X,Y,Z) y x es el vector de desplazamiento de la reacción máxima del modo i.

El enfoque actual es el siguiente (consulte el apéndice B):

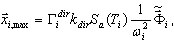( 3.1.2 )

donde 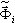indica un vector base (no es necesario que 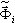sea una aproximación exacta de 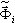, un vector propio exacto de 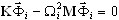, ω_i es una aproximación del valor propio exacto Ωi. Se puede mostrar que (3.1.1) proporciona la misma solución 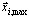que (3.1.2), si 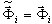(ωi = Ωi). Sin embargo, (3.1.2) no solo es aplicable a solventes directos, sino también al solvente iterativo, ya que no requiere el procedimiento de resolución correspondiente a la matriz de rigidez K. Esta forma es más rápida que (3.1.1) y permite controlar los resultados de forma más segura (suma de esfuerzos - suma de reacciones).

La fórmula que se presenta a continuación se obtiene de (3.1.1).

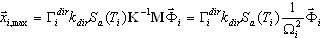( 3.1.3 )

El vector de respuesta modal 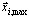describe la respuesta extrema del oscilador SDOF de correspondencia. El siguiente paso debería ser el de definir la respuesta final de la estructura MDOF mediante la media estadística entre modos y entre direcciones de entrada sísmicas.

En las versiones anteriores de Robot, se podían asignar varias direcciones de entrada sísmicas independientes desde el punto de vista estadístico con sus propios multiplicadores de escala en un caso de carga. La media estadística entre direcciones se obtiene de la suma de los valores absolutos y la raíz cuadrada de la suma de las combinaciones de cuadrados en cada modo. Las opciones correspondientes se definen en Preferencias para el proyecto.

La opción Suma de los valores absolutos proporciona lo siguiente:

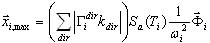( 3.1.4 )

La opción de la raíz cuadrada de la suma de cuadrados permite que el promedio de 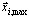de las direcciones de movimiento de entrada sísmicas correspondientes sea como .

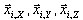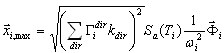( 3.1.5 )

Se puede mostrar que cada componente de 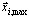es la combinación SRSS de los componentes de correspondencia de ,

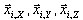donde i =1,2,...,N indica el número de modo o pseudomodo.

La combinación SRSS o CQC entre modos (o pseudomodos) se aplica para obtener la respuesta final de la estructura MDOF considerada después de obtener los vectores de respuesta modal promediados 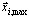, i = 1,2,...,N.

Los vectores de respuesta modal promediados 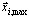, i = 1,2,...,N son los mismos para la suma de los valores absolutos y la raíz cuadrada de la suma de las opciones de cuadrados si la única dirección de entrada sísmica se ha definido para el caso de carga actual (por ejemplo, Kx=Kz=0, Ky=1).

Robot (versión 12.2 y posteriores) guarda el procedimiento mencionado anteriormente de promediar respuestas modales entre direcciones de entrada sísmicas. No obstante, permite llevar a cabo el mejor enfoque. Se recomienda definir una única dirección de entrada sísmica para cada caso de carga y, a continuación, aplicar la combinación SRSS entre las direcciones (correspondientes a las guías normativas estadounidenses) o las denominadas combinaciones "Newmark" (correspondientes a la norma sísmica francesa PS-92 y la norma Eurocódigo-8).

Veamos las nuevas funciones del ejemplo típico siguiente.

En este caso (un único movimiento de entrada sísmico para cada caso de carga), los valores típicos de multiplicadores de escala serán iguales a

Kx=1; Ky=Kz=0 para dir = X (caso de carga S_X).

Kx=0; Ky=1; Kz=0 para dir = Y (caso de carga S_Y).

Kx=Ky=0; Kz=0.7 para dir = Z (caso de carga S_Z; se supone que la intensidad del movimiento vertical es igual a 2/3 de la intensidad del movimiento horizontal).

Se definen tres casos de carga para cada movimiento de entrada sísmico independiente estadísticamente. La respuesta modal para cada uno será la misma que en (3.1.2) (i = 1,2,...,N; dir = X,Y,Z ).

A continuación, es necesario definir el factor de media en todos los modos debido a cada dirección de entrada sísmica: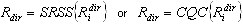

donde 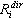hace referencia a algún factor (desplazamiento, fuerza, tensión...) para el modo en posición i debido al movimiento de entrada sísmica en la dirección dir que se corresponde con la respuesta modal 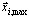(obtenido de 3.1.2);

Rdir es el resultado de la combinación SRSS o CQC sobre todos los modos que se han tenido en cuenta (pseudomodos).

A continuación, se genera un promedio de todas las direcciones de entrada sísmicas activas según la opción seleccionada.

En cada combinación SRSS:

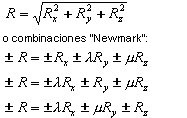
Las opciones de Análisis espectral permiten definir el espectro arbitrario del movimiento de entrada sísmico.

3.7. Análisis sísmico

El método de espectros de respuesta se aplica para el análisis sísmico y espectral. El análisis sísmico se ejecuta sobre la base del análisis espectral (consulte la sección 3.6). Sin embargo, las aceleraciones espectrales Sa = Sa(Ti) se generan para que se correspondan con la norma sísmica seleccionada en lugar de ser asignadas por el usuario (como se hace en el análisis espectral).

La norma sísmica UBC-97 está disponible en Robot (versión 12.0 y posteriores). El análisis del espectro de respuesta se ejecuta de acuerdo con las secciones 1631.5.1 - 1631.5.3 del Código de construcción uniforme (UBC, Uniform Building Code) de 1997. Se pueden cumplir los requisitos de la sección 1631.5.4 ("Elastic Response Parameters may be reduced…") mediante los mecanismos de combinación de Robot. Los componentes de corte básicos Vx, Vy, Vz, los componentes de momento de vuelco Mx y My y el momento de torsión Mz (se supone que el eje OZ es vertical), todos se presentan en la tabla Reacciones en la línea de suma de esfuerzos, tanto para cada respuesta modal como para las combinaciones SRSS y CQC entre modos.

Las siguientes normas sísmicas están disponibles en el programa:

• UBC97
• PS 69 R. 82
• AFPS
• PS 92
• RPA 88
• DM 16.1.96
• EC 8
• IBC 2000
• P100 92
• Norma turca
• Normas chinas
• Norma argentina
• EAK 2000

3.8. Filtros selectivos

Solo los modos que tienen un factor de participación de masas relativamente significativo contribuyen considerablemente a la respuesta sísmica de una estructura. Por lo tanto, basta con tener en cuenta solo estos modos. Los modos restantes con factores de participación de masas pequeños se pueden omitir durante el análisis sísmico. El número de modos derivados suele ser considerablemente mayor que el número que se obtiene de la evaluación de masa efectiva. Por lo tanto, se puede ahorrar espacio en disco y tiempo de cálculo si solo se seleccionan los modos con coeficientes de participación de masas significativos.

Se pueden utilizar dos métodos.

• Cree una lista de modos aceptados para cada dirección de entrada sísmica (caso sísmico) en función de los resultados obtenidos previamente del análisis modal.
• Asigne un valor límite de masa para la masa efectiva modal (se omitirán todos los modos con una masa efectiva modal inferior a ese límite).

El primer método es el más eficaz, aunque requiere un análisis modal previo. El segundo método permite aplicar filtros en la misma ejecución con análisis espectrales y sísmicos, pero suele ocupar más espacio en disco y requiere un mayor esfuerzo de cálculo.

Tenga en cuenta otro ejemplo. Los resultados del análisis modal se presentan a continuación, en la tabla 3.1, donde los casos sísmicos se definen de la siguiente manera: Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) y Dir_Z (Kx=Ky=0; Kz=1).

Tabla 1

Número de modo	Particip. de masas UX (%)	Particip. de masas UY (%)	Particip. de masas UZ (%)	Periodo
1	0.05	12.01	0.004	0.803
2	67.43	0.06	0.005	0.705
3	0.002	0.08	0.07	0.686
4	0.001	0.008	0.009	0.650
5	25.4	0.07	2.06	0.590
6	0.09	68.5	5.05	0.540
7	0.08	10.3	0.06	0.490
8	0.07	0.06	0.56	0.460
9	0.05	0.07	30.56	0.420
10	0.08	0.06	0.25	0.380
11	0.06	0.01	26.7	0.270

Supongamos que tenemos en cuenta todos los modos con un factor de participación de masas superior al 1 %. Los valores de participación de masas correspondientes se indican en la tabla. Tengamos en cuenta que si las direcciones de entrada sísmicas se asignan como ( 1 0 0) para el caso Seism_X, los modos con valores de participación de masas significativos para las direcciones UY, UZ no contribuyen en absoluto a la respuesta sísmica (consulte la sección 3.6):

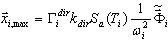
donde dir = X, Y, Z es la dirección de entrada sísmica; 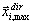es la respuesta máxima para el modo en posición i; 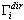es el factor de participación de masas; Sa(Ti) es la aceleración espectral y 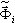es el vector propio en la posición i o el vector base (en el caso del pseudomodo). El multiplicador escalar en el lado derecho de la fórmula anterior 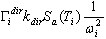define la contribución del modo en posición i a la respuesta sísmica de la dirección dir. En este caso, en el que Ky = Kz = 0, los modos 2 y 5 aportarán contribuciones considerables. Los modos restantes no contribuyen a la respuesta sísmica, debido al multiplicador Kdir cero (dir = Y, Z) y a los valores de participación de masas pequeños para la dirección dir=X. Es posible mostrar, de la misma manera, que en el caso Dir_Y basta con tener en cuenta los modos 1, 6 y 7, mientras que en el caso Dir_Z, los modos son 5, 6, 9 y 11.

Por lo tanto, mediante filtros, el programa puede tener en cuenta únicamente los siguientes modos pertinentes: 2 para el caso Dir_X, 3 para el caso Dir_Y y 4 para el caso Dir_Z. Esto se produce sin una pérdida significativa de contribuciones de masas. Tengamos en cuenta que nos veríamos obligados a aplicar los 11 modos para cada caso si no utilizamos los filtros.

Este enfoque permite reducir el tiempo de cálculo para problemas dinámicos a gran escala (así como los requisitos de espacio en disco y la cantidad de datos de posprocesamiento) sin reducir significativamente la precisión de los resultados en comparación con el método tradicional (en el que no se utilizan filtros selectivos).

Por ejemplo, el problema a gran escala PJG203 contiene 34 266 ecuaciones (el ancho de banda es igual a 990 después de la optimización). El modelo EF correspondiente se presenta en el apéndice 3D (consulte la figura A1). Se debían calcular los 25 pares propios con la matriz de masas coherente y los tres casos sísmicos. El tiempo de cálculo aún alcanzaba aproximadamente 50 horas en un equipo con Pentium PRO (64 MB de RAM, 200 MHZ). El espacio en disco necesario era superior a 1 GB. Además, se ha producido un problema con el módulo de diseño de acero debido a la falta de espacio en disco. (Para calcular las combinaciones SRSS y CQC, era necesario almacenar los datos de 25 modos multiplicados por tres casos sísmicos compuestos por un gran número de grados de libertad para todos los factores, como desplazamientos, esfuerzos internos y tensiones). La aplicación de filtros selectivos permite al programa resolver este problema correctamente.

3.9. Análisis armónico

Se produce la siguiente definición de reacción constante de una estructura a la acción de una carga armónica única:

F(t) = F sin( ωt)

donde w es la pulsación de la carga de excitación. El comportamiento de una estructura se describe como

(K - ω² M) X = F,

donde X es el valor de amplitud del vector de desplazamiento.

3.10. Análisis temporal

El método de descomposición (superposición) modal se lleva a cabo en Robot. Se basa en la representación de un movimiento de estructura como una superposición del movimiento de modos sin acoplar. Por lo tanto, el método requiere que se determinen los valores y los vectores propios. Para ello, se recomienda usar el método de Lanczos. El método de descomposición modal aprovecha las ecuaciones sin acoplar reducidas. Es un enfoque adecuado para analizar la respuesta dinámica de las estructuras sometidas a una acción a largo plazo de cargas dinámicas (por ejemplo, una carga inestable provocada por el uso de equipos en línea o una acción sísmica). Los antecedentes matemáticos y las particularidades de la aplicación se presentan en [3,4,6].

La ecuación (sin amortiguamiento) puede presentar el siguiente formato:

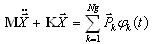(3.11.1)

donde Ng es el número de "grupos de cargas" y φ_k(t) es el historial especificado para el grupo de cargas en la posición k.

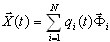(3.11.2)

donde 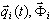corresponde a la coordenada normal en la posición i y al modo (vector propio o vector de Ritz). La sustitución de (3.11.2) por (3.11.1) y la adición de parámetros de amortiguamiento dan lugar a las siguientes ecuaciones modales sin acoplar [3,4,6]

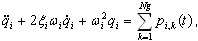(3.11.3)

donde 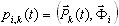, ξi es el parámetro de amortiguamiento modal (por lo general, ξi = 0.05 - 0.2; cuando ξi = 1 indica amortiguamiento crítico, límite entre el movimiento de oscilación y el movimiento periódico) y ωi es frecuencia de vibración natural (pulsación), i=1,2,...,N.

Cada una de las ecuaciones se resuelve numéricamente. Se aplica el método de segundo orden con la selección automática del paso de integración. El vector de desplazamiento resultante para los puntos de tiempo definidos t = t1, t2, ..., t5 se obtiene mediante la sustitución de qi(t5) en (3.11.2).

El método de descomposición modal puede aplicarse para el análisis de la respuesta sísmica. En tal caso, la ecuación de movimiento adopta la siguiente forma:

Y las ecuaciones modales sin acoplar adecuadas:

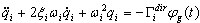(3.11.5)

donde 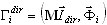es el factor de participación de masas para el modo en la posición i y la dirección de entrada sísmica dir. Cada modo debe normalizarse de la siguiente manera: 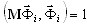. Por último, todos los resultados (desplazamientos, velocidades, aceleraciones, esfuerzos internos y reacciones, etc.) se almacenan solo para los puntos de tiempo definidos t = t1, t2, …, t5. El posprocesador de alto rendimiento permite analizar los resultados del análisis temporal en los modos de diagrama y tabla. En el modo de diagrama, se muestran los factores seleccionados (desplazamiento, aceleración, velocidad, reacciones, esfuerzos de corte, momentos flectores, etc.) para los grados de libertad (DOF) elegidos y se presenta la forma deformada de una estructura en el punto de tiempo seleccionado. El modo de tabla no solo permite ver los valores correspondientes, sino también buscar automáticamente los valores máximo y mínimo entre los factores de respuesta en todos los puntos de tiempo almacenados.

3.11. Análisis modal con fuerzas estáticas

Se tienen en cuenta las pequeñas vibraciones lineales con respecto al estado estático de equilibrio inducido por una carga estática especificada. Se sabe que las fuerzas estáticas influyen en las frecuencias propias de vibración. El análisis modal habitual no tiene en cuenta esa influencia. Sin embargo, sí lo hace cuando el análisis modal tiene en cuenta las fuerzas estáticas.

Las ecuaciones no lineales completas describen el movimiento del estado de equilibrio relativamente estático de un sistema inducido por las cargas estáticas especificada.

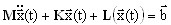(3.12.1)

donde M, K son las matrices de masas y rigidez, L(x(t)) es el operador no lineal, x(t) y b son los vectores de desplazamiento y carga. El procedimiento de linealización consta de lo siguiente:

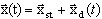(3.12.2)

donde x_st es una parte de la solución común que describe el estado de equilibrio estático y x_d (t) es un vector de pequeños desplazamientos dinámicos. El operador no lineal se puede presentar como descomposición de series de Taylor('s),

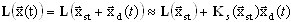(3.12.3)

donde 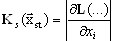es una matriz rígida (tensiones), que es un jacobiano y tiene en cuenta la acción de las fuerzas estáticas. Por lo tanto, se obtiene lo siguiente:

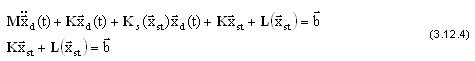
La primera expresión es el resultado de la linealización de desplazamientos dinámicos relativamente pequeños (nota: 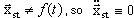) y la segunda describe el estado de equilibrio estático no lineal. Por lo tanto, el movimiento dinámico pequeño con respecto al estado de equilibrio estático es el siguiente:

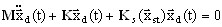(3.12.5)

Vamos a sustituir x_d (t) = Φ e^{i ω t}. Un problema de valores propios se origina a partir de (3.12.5)

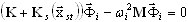(3.12.6)

donde ω_i es el valor propio y Φ_i es el vector propio.

Los cálculos se realizan en dos fases:

1. Análisis lineal (3.12.7) o no lineal (3.12.8) del estado estático de tensión-deformación inducido por una carga estática especificada

   K x_st = b (3.12.7)

   K x_st + L(x_st ) = b, (3.11.8)

   donde x_st es el vector desconocido de estado estático; b es el vector de las fuerzas estáticas especificadas (vector de carga estática); K es la matriz de rigidez, y L (x_st, b) es el operador no lineal. El vector de carga estática b puede ser el resultado de la combinación de varias cargas estáticas. Cabe señalar que un enfoque lineal no cumple exactamente la ecuación de equilibrio no lineal (3.11.8). Por lo tanto, el vector x_st para el estado de equilibrio estático es el resultado de una solución aproximada y la matriz rígida (tensiones) K_s (x_st ) contiene un error. Si la estructura considerada es lo suficientemente rígida y los efectos no lineales aparecen poco, esa aproximación parece ser correcta. De lo contrario, es necesario resolver el problema estático no lineal (3.11.8) (esa técnica no se describe en el manual). Obviamente, el enfoque lineal (3.2.17) es más rápido que el no lineal (3.11.8). En el caso del enfoque lineal, se indica que K_s(x_st ) = G (x_st )= G, donde G es una matriz de rigidez geométrica.

2. Análisis del valores propios (3.12.6)

   Se sabe que los valores positivos de ωi (ωi > 0) representan estados de equilibrio estables y los valores negativos (ωi < 0) representan estados inestables, mientras que el valor cero (ωi = 0) se corresponde con la falta de estabilidad (pandeo).

   La pérdida de la definición positiva de la matriz K + K_s (x_st ) indica que la carga estática supera su valor crítico (pandeo). Se emite la advertencia correspondiente. Se perderá la convergencia durante la ejecución de un problema estático no lineal (3.11.8). Es recomendable interrumpir los cálculos porque los siguientes siguen sin tener sentido.

   Solo el enfoque no lineal está disponible para las estructuras que contienen elementos de cable y de tracción-compresión.

Por ejemplo, tengamos en cuenta la siguiente figura.

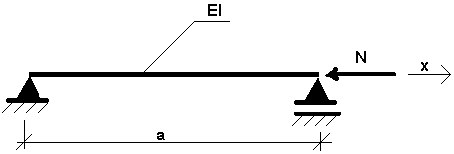
Fig. 3.11.1

N representa la carga estática. La siguiente expresión describe el comportamiento de un sistema de este tipo:

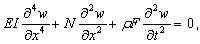( 3.11.9 )

donde w es el desplazamiento de flexión; ρ es la densidad del material, y F es el área de sección transversal.

La solución se buscará como

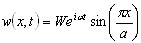( 3.11.10 )

Después de la sustitución de (3.11.10) a (3.11.9), se deriva lo siguiente:

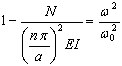, ( 3.11.11 )

donde 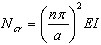es la carga de pandeo y ω₀ es el valor propio para N = 0 (resultado del análisis modal habitual). Por último,

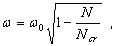( 3.11.12 )

donde ω es el valor propio para el sistema sometido a la acción de una carga estática N. Este resultado se presenta gráficamente en la fig. 3.11.2:

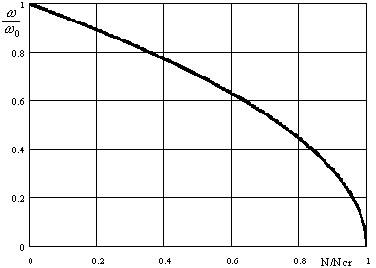
Fig. 3.11.2

La dependencia ω = ω (λ), donde l es un parámetro de carga, para una estructura real suele ser más compleja que la presentada por la expresión ( 3.11.12 ) (consulte [ 1.22 ]).

Apéndice 3A

Métodos de solución de problemas propios

Tenga en cuenta que el mejor método universal para resolver un problema propio no existe actualmente.

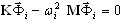, i=1,2,…,n ( A1 )

donde K es la matriz de rigidez, M es la matriz de masa, es el modo propio y ω_i es la pulsación. En la mayoría de los problemas, un método de este tipo utilizará menos recursos (el tiempo de cálculo y el almacenamiento en alta definición) que cualquier otro. Sin embargo, no excluye situaciones diferentes en el caso de otras tareas. Es recomendable aplicar otro método. La versión actual de Robot aborda varios métodos para resolver un problema propio generalizado (A1). Cada una de ellos conlleva sus propias ventajas y desventajas. A continuación, presentamos algunas recomendaciones que se deben tener en cuenta al elegir un método de análisis. Esperamos que, en la mayoría de los casos, conduzcan a los resultados necesarios de la mejor manera posible.

El método de iteración en el subespacio (SI) se lleva a cabo exactamente como se describe en [4], por lo que la descripción de este método no se incluye aquí.

modif.

El método de Lanczos [12,16,17] es un enfoque eficaz y fiable que se utiliza para resolver problemas de valores propios a gran escala (A1). Está disponible cuando se seleccionan solventes Skyline o Sparse Direct.

Este enfoque busca los primeros n valores y modos propios necesarios con cualquier precisión que se desee. Cuanto mayor sea el número de pares propios necesarios, más ventajas presentará el método de Lanczos. Sin embargo, el enfoque implica varias limitaciones.

La matriz T de tres diagonales no debe descomponerse. Es imposible analizar una estructura que consta de dos o más subestructuras no conectadas. En tal caso, cada subestructura se tiene en cuenta por separado o se implementa otro enfoque como, por ejemplo, los métodos de iteración en el subespacio por bloques (BLSI) o de reducción de la base.

La matriz de masas M debe usarse como concentrada con rotaciones o coherente.

No se admite la densidad cero.

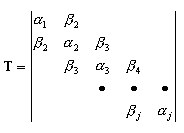
El método de Lanczos utiliza la reducción de la matriz de tres diagonales T

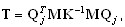, ( A2 )

donde Q_j = {q1, q2, …, qj} es la matriz rectangular; Neq x j y Neq son el número de ecuaciones; j es el número de pasos de Lanczos, y qj es el vector de Lanczos en la posición j. La expresión

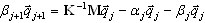( A3 )

genera el siguiente vector de Lanczos qj+1 y define la línea actual de la matriz T.

Por lo tanto, se obtiene el siguiente problema propio reducido:

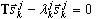, k=1,2,…,j ( A4 )

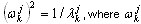es la aproximación en la posición j a ω_k, k=1,2,…,n y n es el número necesario de pares propios. El algoritmo continuará con los cálculos (para aumentar el número j de pasos de Lanczos) hasta que se alcance la precisión necesaria para todos los valores propios necesarios.

El procedimiento de ortogonalización selectiva admite el nivel de ortogonalidad necesarios entre los vectores de Lanczos qj, lo que garantiza la seguridad y la estabilidad numérica del proceso de cálculo. Utilizamos métodos económicos para proporcionar ortogonalización selectiva y resolver el problema de valores propios reducido (A4) mediante la duplicación de iteraciones de QR con cambios.

Los vectores propios de origen se determinan mediante la siguiente fórmula:

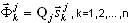( A5 )

Los detalles se presentan en [12,16,17].

Método de reducción de la base

Este método [4, 5] se conoce como método de Rayleigh-Ritz mejorado [4]. En [5], se presenta un método de este tipo, una variante discreta del método de Bubnov-Galerkin. Este algoritmo permite obtener valores aproximados de los primeros pares propios si se conoce alguna información sobre ellos. Para este método, es necesario aplicar un grado principal de libertad (MDOF) para obtener el sistema reducido. De este modo, se puede controlar el proceso de creación del modelo reducido. Es una herramienta muy eficaz para quienes tienen experiencia en el análisis dinámico de estructuras y se ocupan de un tipo de estructuras similar con un comportamiento conocido. Este método permite excluir grados de libertad (DOF) no deseados del modelo reducido y rebaja el problema complejo inicial con un gran número de grados de libertad a una forma reducida. Esto se consigue con un número considerablemente menor de grados de libertad. La experiencia relativa al análisis dinámico de la estructura muestra que el usuario puede encontrar algunos problemas cuando los métodos de reducción automática (se tienen en cuenta BLSI, SI y Lanczos) dan lugar a un proceso de cálculo muy complejo. Por ejemplo, los modos de vibración local de las barras individuales pueden provocar problemas graves, ya que el proceso de cálculo busca automáticamente los pares propios sin ninguna selección. Esto se debe tener en cuenta en estructuras de carácter real en la mayoría de los casos. De lo contrario, estas vibraciones locales quedarán restringidas por algunas limitaciones ignoradas en el modelo MEF o aportarán poco al movimiento general del sistema. Normalmente, el porcentaje de masa es muy pequeño para estas vibraciones locales. El uso de métodos exactos en este caso dará lugar a las dificultades mencionadas anteriormente. Sin embargo, la implementación del método de reducción de la base aproximada puede simplificar considerablemente el proceso de cálculo.

Este método tiene las siguientes limitaciones.

El usuario debe asignar los siguientes MDOF: los nudos y las direcciones principales. Se presupone que solo se pueden asignar los desplazamientos (no las rotaciones) como grados de libertad principales.

El algoritmo se implementa para cualquier tipo de matriz de masas. Sin embargo, el tipo de matriz de masas concentrada sin rotaciones ofrece más ventajas con respecto al tiempo de cálculo.

• La verificación de secuencia Sturm no está disponible. Solo hay una forma de comprobar la convergencia. Aumente el número de MDOF (asigne nudos y direcciones principales adicionales), resuelva este problema una vez más y compare los valores propios.

Este método transforma el problema de valores propios a gran escala de origen para el modelo MEF

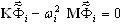(A6)

(A1) en un problema de valores propios para el modelo reducido

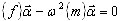(A7)

donde {f} es la matriz de influencia; {m} es la matriz de masas generalizada para un modelo reducido,

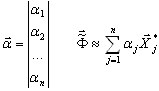(A8)

donde n es un número de grados de libertad de un modelo reducido. La base de estas transformaciones es una solución estática obtenida para los estados unitarios adecuados: las fuerzas nodales unitarias se aplican en consecuencia en cada nudo principal, en la dirección principal seleccionada. Se ha resuelto un problema estático a gran escala para n lados de la derecha:

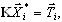i = 1, 2, …, n (A9)

donde Ti es el vector de carga correspondiente a i, la carga unitaria. El usuario debe asignar nudos y direcciones principales. El programa realizará todas las operaciones solicitadas.

El problema reducido de valores propios se resuelve mediante el método de Jacobi, que conduce a las frecuencias aproximadas ω_i y a los modos 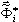, i=1,2,...,n. Los detalles de este enfoque se presentan en [5].

Método de iteración en el subespacio por bloques

El método de iteración en el subespacio por bloques (BLSI) resuelve un problema generalizado de valores propios (A1). Está disponible para los solventes Skyline y Sparse Direct. Es un enfoque sólido y eficaz. Se recomienda encarecidamente aplicar este método cuando se produzca un problema a gran escala y sea necesario obtener un gran número de pares propios (más de 10). El método BLSI se puede aplicar para el análisis de estructuras independientes. Todos los tipos de matrices de masas (concentradas sin rotaciones, concentradas con rotaciones y coherentes) están disponibles durante el análisis modal. El área de aplicación de este enfoque está limitada por el modo Modal. El modo sísmico y el pseudomodo siguen estando disponibles si se elige Lanczos.

La verificación de secuencia Sturm se realiza para detectar los valores propios omitidos. El método BLSI controla la continuidad de los valores propios convergentes. La discontinuidad de los valores propios convergentes indica la presencia de valores propios omitidos. Sin embargo, la continuidad de los valores propios convergentes no proporciona una garantía absoluta de que falten los valores propios omitidos. Sin embargo, los resultados de numerosos cálculos indican que, en la mayoría de los casos, las verificaciones de secuencia Sturm no detectan valores propios omitidos cuando BLSI garantiza la continuidad de la convergencia. La gran ventaja de este método es la posibilidad de evitar un procedimiento de verificación de Sturm que lleve mucho tiempo si no se necesita una garantía completa de los valores propios omitidos. Si se cumple la discontinuidad de los valores propios convergentes, aparece el siguiente mensaje (consulte la fig. A1).

La idea principal del método BLSI [1-3] consiste en iteraciones de vectores simultáneas en el subespacio de tamaño fijo. Cada vector convergente se elimina del subespacio de trabajo (bloque) y, en su lugar, se añade un nuevo vector inicial. La ortogonalidad de los vectores convergentes se garantiza en cada paso de la iteración.

Se recomienda la aplicación del procedimiento de aceleración por desplazamiento [1,4] durante el análisis modal cuando la convergencia es lenta.

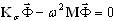, ( A10 )

donde K_σ= K - σ M, σ es el valor de desplazamiento. Al comienzo del análisis, se presupone que σ = 0. Se realiza la actualización automática del valor de desplazamiento si no aparecen nuevos valores propios convergentes a través del número aceptado de pasos de iteración de control. Por ejemplo, aceptemos que el número de pasos de control es igual a 5. A continuación, aparecen cinco valores propios convergentes después de cuatro iteraciones. El valor de desplazamiento se mantiene en σ = 0. En la siguiente iteración, los valores propios del paso 3 convergen. El valor de desplazamiento se mantiene en σ = 0. A continuación, durante los cinco pasos de iteración, no convergen los modos propios. El algoritmo detecta de nuevo la "convergencia lenta"; adopta σ = ω₈ ², actualizaK_σ = K - σ M y factoriza la matriz desplazada actualizada K_σ. A continuación, después de dos pasos de iteración, convergen dos modos propios. El valor de desplazamiento se mantiene en ω₈ ². A continuación, durante los cinco pasos de iteración siguientes, no converge ningún valor propio. El algoritmo vuelve a detectar una "convergencia lenta" y utiliza ω₁₀ ², actualiza K_σ = K - σ M y factoriza la matriz desplazada actualizada K_σ.

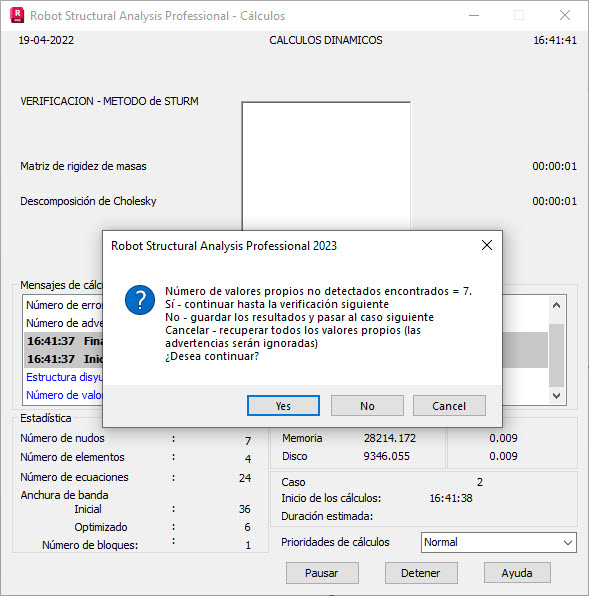
Fig. A1. Detección de la discontinuidad de los valores propios convergentes mientras se ejecuta el método BLSI.

Si se indica:

• Sí, los cálculos continuarán hasta que aparezca el siguiente valor propio convergente. A continuación, se realizará la siguiente verificación.
• No, los resultados se guardarán y los cálculos pasarán al siguiente caso.
• Cancelar, los cálculos continuarán siempre que se garantice la continuidad completa de los valores propios convergentes. Se omitirá la advertencia.

Estas no son todas las recomendaciones. Puede aplicar o no las aceleraciones por desplazamiento. Recuerde que la aplicación del desplazamiento adecuado es una herramienta eficaz de aceleración de la convergencia. De lo contrario, cada factorización de la matriz K_σ actualizada puede ser un procedimiento que lleve mucho tiempo en completarse, sobre todo, para un problema a gran escala. Por lo tanto, la decisión final sobre la aplicación del desplazamiento debe tomarse según la experiencia y la intuición del usuario.

En el siguiente ejemplo, se muestra la ventaja de la aplicación de desplazamiento. El modelo de cálculo se muestra en la figura A2. El método BLSI extrae 50 modos propios. Se ha seleccionado el solvente Skyline. Se acepta la tolerancia 1.0e-09. Resulta que la convergencia que comienza con el modo 38 sigue siendo tan lenta que, durante 20 minutos de cálculos, no se obtienen resultados. Una vez activada la aceleración por desplazamiento (se ha aceptado la actualización de un desplazamiento en cada uno de los cinco pasos de iteración no convertidos), el tiempo de cálculo sigue siendo de 50 segundos. Obviamente, se pueden presentar numerosos ejemplos si la aplicación del desplazamiento reduce el número de iteraciones. Sin embargo, aumenta el tiempo de cálculo. Es recomendable activar las aceleraciones por desplazamiento cuando un enfoque convencional (los desplazamientos están desactivados) genera un gran número de iteraciones en algunas fases de la ejecución de BLSI.

Fig. A2 Estructura de marco espacial

Método de Lanczos modificado

Este es un ajuste del método de Lanczos en el pseudomodo para el solvente iterativo. El método de Lanczos habitual requiere la factorización de una matriz de rigidez (consulte la sección A3). Cuando se soluciona un problema a gran escala, la factorización de la matriz de rigidez sigue siendo muy lenta. En el caso de problemas grandes (más de 100 000 ecuaciones), no solo la factorización de una matriz de rigidez requiere un enorme esfuerzo de cálculo, sino que la solución de un conjunto de ecuaciones de la matriz adecuadamente factorizada también es costosa.

El método de Lanczos modificado se basa en el enfoque iterativo. Evita el almacenamiento, el montaje y la factorización de una matriz de rigidez a gran escala. La evaluación de cada vector de Lanczos requiere aproximadamente el mismo esfuerzo de cálculo que la solución de un problema estático con un único lado derecho. En cuanto al pseudomodo, reduce el número necesario de vectores de Lanczos en comparación con el modo Modal que se aplica al ejecutar el método de Lanczos modificado.

Se aplica al solvente iterativo AEBEIS (consulte [7, 8]) para la generación de vectores de Lanczos. Se recomienda utilizar la técnica ICCF (factorización incompleta de Cholesky) tanto para el preacondicionamiento de agregación multinivel [7, 8, 18-20] como para el método habitual no multinivel. Garantiza la rapidez de las operaciones durante las evaluaciones del producto matriz-vector y la resolución rápida del preacondicionamiento de la correspondencia. Hay que tener en cuenta que la tolerancia adoptada para el solvente iterativo (Preferencias para el proyecto > Análisis de estructura > Parámetros) determina la precisión de la evaluación de los vectores de Lanczos. Por lo general, basta con aceptar 1.0e-04. Cuantos más nudos se tengan en cuenta, más cerca estarán los vectores bajos de Ritz de los modos propios correspondientes y se obtendrá una suma más completa de las masas modales.

Método de gradiente conjugado preacondicionado (PCG)

Es recomendable usar el método PCG [9-13] para la definición de un pequeño número de modos propios en el modo Modal cuando se aplica un solvente iterativo. Puede resultar muy útil para asignar una carga de viento o para comprobar algunos modos bajos obtenidos mediante el método PCG_Ritz. Están disponibles todos los tipos de preacondicionamiento (consulte Herramientas > Preferencias para el proyecto > Iterativo > Parámetros) definidos para el análisis estático. Se pueden utilizar todos los tipos de matrices de masas (coherentes, concentradas con rotaciones y concentradas sin rotaciones).

Un método de gradiente conjugado preacondicionado se basa en la minimización directa del cociente de Rayleigh

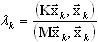(A11)

mediante el enfoque de gradiente, donde k es el número de iteración y λ_k es la aproximación correspondiente de un valor propio. El enfoque de gradiente busca ese valor del parámetro α_k que garantiza el valor mínimo de λk a partir de (A11):

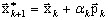(A12)

donde p_k es un vector de dirección conjugada. La búsqueda del valor adecuado de α_k (consulte las seccione 9-13) conduce a lo siguiente:

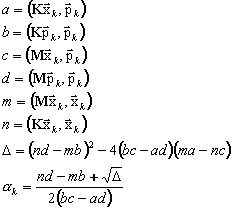
El preacondicionamiento B se aplica para acelerar la convergencia

B z_k+1 = r_k+1 -> z_k+1 (A13)

La dirección del gradiente se define como

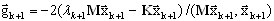(A14)

La nueva dirección de conjugación se define como

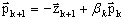(A15)

donde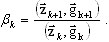

Las iteraciones se realizan hasta

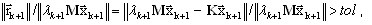(A16)

donde tol es la tolerancia deseada. Por lo general, tol = 1.0e-02 garantiza una muy buena precisión para fines de ingeniería. Hay que recordar que el coeficiente de convergencia (A16) se calcula con una norma muy estricta (consulte la parte relativa a la precisión de los cálculos). La tolerancia mencionada anteriormente proporciona una precisión de valores propios no inferior a 1.0e-04.

Cuando converge un primer par propio, este se almacena como resultado final y comienzan las iteraciones para calcular el siguiente. El procedimiento de ortogonalización de los vectores propios definidos anteriormente en cada paso de iteración se emplea para evitar la duplicación de los pares propios. Este proceso se aplica hasta que se obtienen todos los pares propios deseados.

La forma más eficiente de aceleración de convergencia para PCG es la implementación de un buen preacondicionamiento. Todos los tipos de preacondicionamiento que se presentan para un solvente iterativo están disponibles para el método PCG. Se recomienda estrictamente aplicar el preacondicionamiento multinivel [18-20] o el preacondicionamiento no multinivel con el suavizado ICCF [9-12] del solvente AEBEIS [7, 8].

Método de gradiente Ritz (PCG_Ritz)

El método PCG_Ritz [8] es un método rápido de definición de un conjunto de vectores de Ritz en el pseudomodo cuando se selecciona el solvente iterativo. Este enfoque puede ser muy fructífero para el análisis sísmico y espectral de estructuras de tamaño medio que incluyan (10 000 - 60 000) ecuaciones.

Se basa en la generación del sistema ortogonal de vectores base. El enfoque de gradiente con preacondicionamiento de agregación multinivel sobre la base de la técnica de elemento por elemento se aplica para minimizar el cociente de Rayleigh para cada paso de la preparación del vector base. Garantiza la evolución del vector base de la consecuencia hacia el modo propio más bajo sin agregación ni descomposición de una matriz de rigidez a gran escala. Este método suele ser más eficaz para el análisis de la respuesta dinámica en comparación con el método clásico de superposición modal, sobre todo, para el análisis de la respuesta sísmica. El método propuesto permite aplicar tipos arbitrarios de elementos finitos debido al enfoque de agregación y garantiza una solución rápida y un ahorro en cuanto al almacenamiento en disco provocado por el uso de EBE. Este método es especialmente eficaz cuando se utiliza una matriz de masas coherente.

El problema de valores propios especificado es el siguiente:

Kφ - λM φ = 0 (A17)

donde K, M son las matrices de rigidez y masas respectivamente, φ es el vector propio y λ es el valor propio. Se describirá el procedimiento de evolución del conjunto de vectores base x0, x1, ..., xn hacia el modo propio más bajo. El enfoque de gradiente preacondicionado se aplica para minimizar el cociente de Rayleigh

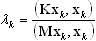(A18)

donde 0 ≤ k ≤ n, k es el número de pasos de evolución; n+1 es el número de vectores base, que definen el tamaño del tramo de subespacio perteneciente a (x0, x1, ..., xn); n+1 << N, donde N es el número de grados de libertad para el problema que se tiene en cuenta (A17). Muy a menudo parece que el problema de valores propios considerado está mal acondicionado. En tal caso, la evolución del vector base de la consecuencia xk hacia el modo propio más bajo será muy lenta. El operador de preacondicionamiento B se aplica para mejorar esa situación. La expresión B z_k = r_k -> z_k indica la resolución de un determinado conjunto de ecuaciones del vector de correspondencia zk, donde B es un operador de preacondicionamiento y r_k = Kx _k - λ_k M x_k es un vector residual correspondiente.

Los vectores base cumplen las siguientes condiciones de ortogonalidad:

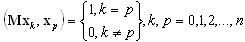(A19)

El problema de origen a gran escala (A17) se reduce al problema propio de subespacio.

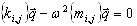(A20)

Las matrices de proyección del subespacio se definen como {k_ij} = {Kx_i, x_j} y {m_ij} = {Mx_i, x_j} = U, donde U es una matriz unitaria.

Los vectores de Ritz v₁, v₂, …, v_n+1 para los vectores base derivados x0, x1, …, xn y las aproximaciones correspondientes de las frecuencias ω₁, ω₂, …, ω_n+1 se utilizan para la superposición de la respuesta dinámica estructural.

El procedimiento de la evolución de los vectores base x_k, k = 0, 1, ..., n hacia el modo propio más bajo es muy cercano al paso correspondiente del método de iteración de gradiente preacondicionado para la solución del problema propio. Es un hecho conocido que la convergencia de los métodos de iteración preacondicionados depende considerablemente de las propiedades del operador preacondicionado B. Este operador debe definirse positivamente; permite la solución económica B z_k+1 = r_k+1 y satisface la condición numérica C ( B^-1 K) -> 1 de la mejor forma posible.

El último requisito en el caso del método de gradiente Ritz garantiza una buena aproximación de la parte baja de los modos propios.

Este método solo está disponible para el enfoque iterativo multinivel, lo que garantiza una buena calidad de preacondicionamiento. Se utilizan la técnica de preacondicionamiento EBE (elemento por elemento) y la ICCF. La calidad de los vectores de Ritz generados de esa forma depende considerablemente de las propiedades del operador de preacondicionamiento B (consulte A13 y [8]). Dado que el modelo de nivel bajo aproxima eficazmente los modos de vibración bajos, los vectores de Ritz en el nivel alto son una buena aproximación de los correspondientes vectores propios (consulte [8]). Por lo tanto, la calidad de los resultados obtenidos mediante este método depende considerablemente de la capacidad del modelo de nivel bajo para mantener la similitud con el modelo MEF especificado (el denominado nivel alto). Por lo general, un único nivel de agregación garantiza una buena aproximación. Cuando el número de niveles de agregación es superior a uno, no se garantiza la calidad de los resultados. Es una limitación principal de la aplicación de este método para el análisis de un problema a gran escala cuando el número de ecuaciones supera las ~60 000.

Si la matriz de preacondicionamiento B = K (el nivel bajo es idéntico al alto), el método de gradiente Ritz propuesto pasa exactamente al método de Lanczos (consulte [8]). Los antecedentes matemáticos se presentan en [8].

Análisis modal: precisión de los cálculos

El problema generalizado de valores propios se define como

Kφ - λM φ = 0 (A17)

donde K, M son las matrices de rigidez y masas respectivamente, y {φ, λ} son los pares propios (modo natural de vibración y valor propio). Se definen dos tipos de vectores residuales:

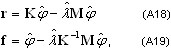
donde {φ, λ} son realmente pares propios calculados que contienen algunos errores de cálculo. La primera expresión define el vector residual en términos de fuerzas y la segunda, en términos de desplazamientos.

Se utilizan cuatro criterios diferentes para estimar el error de cálculo de los vectores propios.

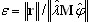• . Se trata de un criterio muy estricto. Normalmente ε ≤ 0.01 significa que los cuatro primeros dígitos del valor propio se han definido con exactitud. Se aplica solo a PCG si se ha seleccionado el solvente iterativo.
• e = (r, φ). Se trata de un criterio ligeramente más blando que el anterior. Se aplica al método de Lanczos modificado si se ha seleccionado el solvente iterativo.
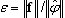• . Es un criterio blando porque la convergencia de los desplazamientos en una definición especificada de MEF suele ser más rápida que la convergencia de los esfuerzos internos. Se utiliza para BLSI, SI y Lanczos si se han seleccionado los solventes Skyline o Sparse Direct.
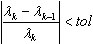• , donde λk, λk-1 son dos valores propios sucesivos en los pasos de iteración k, k-1 y tol indica la tolerancia de los valores propios adoptada en el cuadro de diálogo Parámetros del análisis modal. Se utiliza como criterio intermedio mientras se ejecutan los métodos BLSI, SI y de Lanczos (solventes Skyline o Sparse Direct) en el modo Modal. Este criterio no es rígido, aunque sí muy rápido. El uso de (4) permite reducir considerablemente el tiempo de cálculo de los métodos BLSI, SI y de Lanczos, sobre todo, para los problemas a gran escala. Una vez completado el análisis de valores propios, se aplica el criterio (3) como verificación final de la precisión. El usuario debe examinar la columna Precisión de la tabla donde se muestra el valor 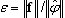. Si la precisión es insuficiente para un modo propio, es necesario repetir el análisis de valores propios con una tolerancia mayor para los valores propios tol.

En la siguiente tabla, se resumen las consideraciones indicadas anteriormente. El símbolo N/A significa que no se produce la comprobación de convergencia correspondiente. Los resultados de la verificación final solo se obtienen una vez y se muestran en la columna Precisión de la tabla. La comprobación de convergencia durante los cálculos se realiza varias veces.

	Solventes directos		Solvente iterativo
Tipo de criterio	BLSI, SI, Método de Lanczos	Método de reducción de la base	Lanczos modificado	PCG_Ritz	PCG
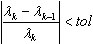
Durante los cálculos		N/A	N/A	N/A
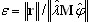
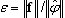
Verificación final		N/A	e = (r, j)	N/A

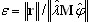
Cabe señalar que Lanczos para el modo Sísmico genera una comprobación de convergencia 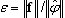a través de cada uno de los 20 pasos de Lanczos. Los métodos de reducción de la base y PCG_Ritz son los métodos de Ritz. Dado que no es el enfoque iterativo, no se realiza la verificación de la precisión.

Si la precisión de algunos modos después del cálculo parece ser insuficiente, es necesario realizar lo siguiente:

Solventes directos		Solvente iterativo
BLSI, SI, Método de Lanczos (modo Modal)	Método de reducción de la base	Lanczos modificado	PCG_Ritz	PCG
Reduzca la tolerancia (tol) en el cuadro de diálogo Parámetros del análisis modal.	Aumente el número de nudos y direcciones base.	Aumente el número de entradas. Reduzca la tolerancia (tol) en el cuadro de diálogo Parámetros del solvente iterativo.	Aumente el número de entradas. Reduzca el número de niveles de agregación. Aumente el número de iteraciones internas.	Reduzca la tolerancia (tol) en el cuadro de diálogo Parámetros del análisis modal.

Apéndice 3B

El enfoque de pseudomodo

Las ecuaciones de movimiento de origen para cargas sísmicas presentan el siguiente formato:

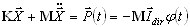(B1)

K, M: las matrices de rigidez y masas;

I dir es el vector de unidad de dirección y φ(t) es el historial de tiempo de la aceleración del suelo.

La solución se busca como:

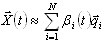(B2)

donde q_i son los vectores base del tamaño y Neq es el número de ecuaciones del modelo EF de origen.

Estos vectores deben cumplir los siguientes requisitos:

• Condiciones de contorno estático y cinemáticas
• Independencia lineal
• Integridad básica

Se pueden adoptar los vectores de Lanczos o cualquier vector obtenido para fuerzas nodales concentradas de unidad (método de reducción de la base para solventes directos o el método de gradiente de Ritz, PCG_Ritz).

La proyección en el subespacio se describe como:

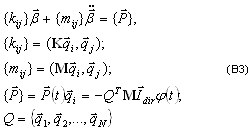
Observemos que β es de tamaño N; la matriz Q es de tamaño NeqxN.

Las ecuaciones del subespacio (B3) se resolverán mediante la descomposición de los vectores propios (en el subespacio definido por Q = {q1, q2, ..., qN}).

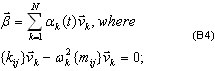
Observemos que la descomposición (4) es una expresión exacta porque el subíndice k presupone valores de 1 a N sobre todo el tamaño del subespacio Q.

La sustitución de (B4) por (B3) conduce al conjunto sin acoplar de ecuaciones.

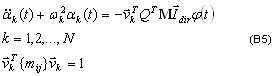
Tengamos en cuenta

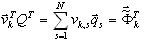(B6)

Por lo tanto, (B5) se puede presentar como

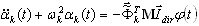(B7)

donde k=1,2,…,N.

Apliquemos el método de espectros de respuesta a las ecuaciones sin acoplar (B7)

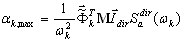(B8)

donde son la respuesta máxima para el modo del subespacio k y la función de aceleración espectral, respectivamente.

Vamos a sustituir (B8) por (B4) y, a continuación, por (B2):

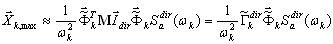(B9)

Debe tenerse en cuenta que para N -> Neq:

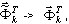
ω_k -> Ω_k

donde Ωk, 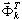son el par propio exacto de los problemas propios de EF de origen

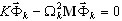(B10)

y 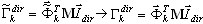, donde 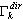es el factor de participación de masas para el modo propio k.

Conclusiones

1. El enfoque propuesto no requiere las aproximaciones "buenas" 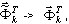, ω_k -> Ω_k. Es posible que 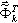, ω_k se aproxime a 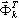, Ω_k con precisión arbitraria.
2. El enfoque propuesto no es peor que el conocido método de descomposición modal (superposición). Ambos métodos constituyen casos específicos del método de proyección común y convergen en la solución "exacta" cuando N -> Neq. (Esta afirmación no es válida exactamente para el método de espectros de respuesta, ya que este método es de carácter estadístico y su convergencia a la solución exacta tiene lugar cuando N -> ∞. Es evidente que, para N > Neq, surgirá un conflicto de cálculo debido a que el número de vectores base no puede superar Neq. Por lo tanto, es posible obtener diferentes soluciones para vectores base diferentes cuando N = Neq. Es una particularidad del método de espectros de respuesta. Para los métodos distintos al de espectros de respuesta, la convergencia completa tiene lugar cuando N = Neq. La convergencia en el caso del método de espectros de respuesta debería tenerse en cuenta solo en el sentido estadístico, ya que este método constituye un enfoque estadístico orientado a obtener una solución media una vez que se ha perdido el análisis temporal. Debido a ello, el término "solución exacta" debe aplicarse con precaución).
3. ¿Qué base es mejor? ¿Los vectores de Ritz o propios? Debe existir una base que garantice una mejor convergencia con la solución "exacta" (N = Neq) mediante el menor número de funciones base N. La cuestión debe resolverse mediante el estudio de ejemplos prácticos.

   Por lo general, la primera parte de los pares 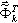, ω_k proporcionan buenas aproximaciones a los pares propios de correspondencia 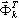, Ω_k (Es posible determinar la precisión de cada par en la columna Precisión del listado de salida). Solo la última parte de los pares 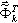, ω_k proporcionan malas aproximaciones a los pares propios exactos y pueden considerarse "pseudomodos" (desde el punto de vista de la norma sísmica francesa PS-92).

4. El uso de todo el subespacio Q = {q1, q2, …, qN} garantiza el aumento rápido del porcentaje de masas. En el caso de los modos Modal y Sísmico, solo se utiliza una parte de este subespacio.

Apéndice 3C

Ejemplos de aplicación del modo Sísmico y los pseudomodos.

Es evidente que hay muchos tipos de problemas sísmicos y espectrales en los que es difícil obtener un porcentaje suficiente (70 - 90 %) de masas. Es posible resolver los llamados problemas buenos mediante métodos conocidos.

• Asigne un número arbitrario de N modos.
• Calcule los primeros N modos secuenciales mediante el modo Modal.

Sin embargo, para los problemas difíciles, es posible que este enfoque no esté accesible. Tengamos en cuenta, por ejemplo, los problemas de Coreal o Museo. Son modelos MEF preparados por ingenieros franceses. Se muestra una masa efectiva para un número diferente de modos propios definidos. Se utiliza el modo Modal (método de Lanczos).

El historial de convergencia del problema de Coreal

Número de modos convergentes	Masa efectiva
44	< 1%
62	12%
75	38%
89	60%
116	74%
154	77%
179	80%

El historial de convergencia del problema de Museo

Número de modos convergentes	Masa efectiva
41	20%
106	40%
119	42%

Por ejemplo, el 80 % indica que, para dos direcciones, las sumas de masas no son menores que el número especificado. El modo Modal genera modos propios, mientras se alcanza la masa efectiva adoptada o se agota el límite superior de modos asignado. La solución final del método de espectros de respuesta se obtiene en forma de superposición estadística de vectores propios.

En ambos problemas considerados, el número de grados de libertad es inferior a 2000. Se considera que esos problemas son pequeños (con respecto al número de grados de libertad). En los casos de problemas medianos y grandes (difíciles), es posible que tanto el modo Modal como el Sísmico resulten inaplicables en la práctica debido al carácter expansivo del proceso de cálculo. En tales casos, se recomienda la aplicación del pseudomodo. A continuación, se presenta el historial de convergencia de los problemas de Coreal y Museo.

Historial de convergencia del problema de Coreal

Número de vectores base	Masa efectiva
10	58%
20	67%
40	70%
80	80%

Historial de convergencia del problema de Museo

Número de vectores base	Masa efectiva
10	60%
20	66%
40	71%

Nota: Es necesario definir aproximadamente de 130 a 150 vectores de Lanczos para obtener 80 vectores propios para el modo Modal. El esfuerzo de cálculo en el pseudomodo es considerablemente menor (aproximadamente de 3 a 5 veces).

La convergencia de los resultados en el pseudomodo se muestra en el siguiente problema. La siguiente tabla presenta los valores máx./mín. resultantes de la combinación CQC del modo Modal y el pseudomodo.

Modo	UX (cm)	UY (cm)	UZ (cm)	Masa efectiva
Modal	5.52002e-00	5. 88293e-00	5.83013e-00	81%
Pseudomodo, Nvect = 10	5.58710e-00	5. 89055e-00	5.00224e-00	80%
Pseudomodo, Nvect = 20	5.52937e-00	5.88870e-00	6.08661e-00	91%

Nvect es el número de vectores base.

Apéndice 3D

Aplicación de métodos de análisis modal para solucionar problemas a gran escala

Ejemplo 1

Comparación del tiempo de cálculo para los métodos BLSI y de Lanczos. Se tienen en cuenta diferentes números de modos propios.

Solvente aplicado: Sparse Direct. Tipo de matriz de masas: concentrada con rotaciones.

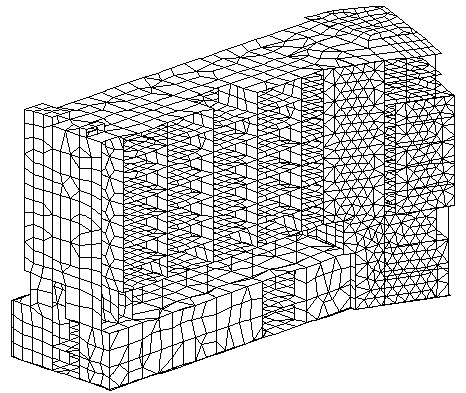
Fig. D1. Modelo de un hotel. Número de nudos: 6359. Número de elementos: 7264. Número de ecuaciones: 37 806.

Tabla D1. Comparación de resultados

BLSI		modif.
f (Hz)	Precisión	F (Hz)	Precisión
2,794e-001	1,082e-006	2,794e-001	5,680e-015
1,388e+000	1,389e-004	1,388e+000	2,199e-013
1,520e+000	7,847e-004	1,520e+000	8,193e-012
1,644e+000	2,469e-004	1,644e+000	4,497e-013
1,747e+000	2,691e-004	1,747e+000	5,455e-014
1,776e+000	3,092e-004	1,776e+000	9,127e-013
1,806e+000	3,153e-004	1,806e+000	6,621e-013
1,818e+000	6,383e-004	1,818e+000	3,656e-012
2,622e+000	1,565e-003	2,343e+000	2,047e-011
2,634e+000	1,383e-003	2,622e+000	1,223e-005

Dado que no se realiza la verificación de Sturm, la omisión del par propio se produce entre los modos octavo y noveno cuando se aplica BLSI.

Tabla D2. Duración de la extracción de modos (en segundos)

Método	10 modos	50 modos	100 modos
BLSI	735	6029	23572
modif.	1472	12637	25271

Factorización de la matriz: 841 s

Los métodos avanzados (BLSI, Lanczos) basados en un potente solvente Sparse Direct generan rápidamente la factorización de la matriz y extraen un gran número de modos propios. Los cálculos se realizaron en un equipo P-350 (256 MB de RAM).

Ejemplo 2

Aplicación de diferentes métodos a la solución del problema de PJG203. El modelo contiene uniones rígidas que conducen al uso de una matriz de masas coherente. Se han extraído 25 pseudomodos.

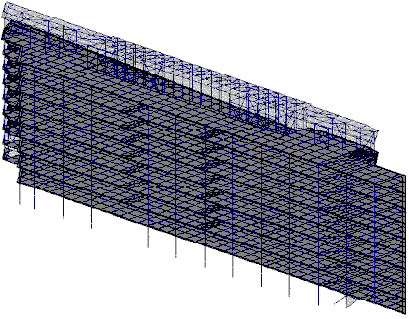
Fig. D2. Problema de PJG203. Número de nudos: 5945. Número de elementos: 11 471. Número de uniones rígidas: 22. Número de nudos compatibles: 302. Número de ecuaciones: 34 266.

Tabla D3. El tiempo de cálculo, el almacenamiento en disco, las diez primeras frecuencias y la precisión correspondiente para distintos métodos.

Método	Tiempo (s)	Disco duro (MB)	Frecuencias (Hz)	Precisión
Skyline	61 633	597	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.829e+000 3.033e+000 3.209e+000 3.595e+000	8.043e-015 1.025e-013 1.031e-013 1.712e-006 5.566e-006 6.331e-008 3.538e-001 3.052e-005 9.086e-005 4.498e-003
Sparse	4 435	99	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.825e+000 3.033e+000 3.209e+000 3.595e+000	3.522e-012 2.689e-011 1.159e-010 1.735e-006 5.639e-006 6.419e-008 3.520e-001 3.034e-005 9.938e-005 4.386e-003
Lanczon modif.	3 459	24	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.791e+000 3.033e+000 3.209e+000 3.595e+000	3.719e-004 3.891e-004 6.601e-004 1.454e-003 1.875e-003 2.946e-003 3.364e-003 3.923e-003 2.175e-002 1.580e-001
PCG_Ritz	1 521	24	1.266e+000 1.350e+000 1.467e+000 2.445e+000 2.446e+000 2.446e+000 2.805e+000 3.035e+000 3.381e+000 3.566e+000	N/A: PCG_Ritz no es un método iterativo, es un método de Ritz. Por lo tanto, se obtienen pseudomodos en lugar de los modos propios "exactos".

Se han utilizado los siguientes parámetros para el método de Lanczos modificado: solvente iterativo AEBEIS (modo multinivel); preacondicionamiento ICCF; 2 niveles de agregación; 4 iteraciones internas, tol = 1.0e-04, y precisión de generación de los vectores de Lanczos.

Se han adoptado los siguientes parámetros para el método PCG_Ritz: solvente iterativo AEBEIS multinivel; preacondicionamiento ICCF; 1 nivel de agregación, y 4 iteraciones internas.

Las frecuencias convergentes aparecen marcadas en rojo. Si la precisión (consulte el apéndice 3A) de una norma relativa de un vector residual para un modo determinado es inferior a 5.0e-02, esa norma puede considerarse totalmente convergente al vector propio correspondiente. Por lo tanto, las frecuencias marcadas en rojo se consideran los valores exactos para un modelo discreto determinado. La estimación de errores para el método PCG_Ritz se presenta en la tabla D4. Se puede concluir que los resultados obtenidos por el método PCG_Ritz proporcionan una aproximación suficientemente buena para los fines de ingeniería y este enfoque puede utilizarse para la estimación rápida del comportamiento sísmico.

Los métodos avanzados permiten reducir considerablemente el tiempo de cálculo y los requisitos de almacenamiento en disco sin ninguna pérdida grave de integridad.

Tabla D4. Cálculo de errores para el método PCG_Ritz

Frecuencia "exacta"	Resultados de PCG_Ritz	Error (%)
1.175e+000	1.266e+000	7.7
1.337e+000	1.350e+000	1.0
1.454e+000	1.467e+000	0.9
2.445e+000	2.445e+000	0.0
2.445e+000	2.446e+000	0.0
2.628e+000	2.446e+000	7.0
2.791e+000	2.805e+000	0.5
3.033e+000	3.035e+000	0.1
3.209e+000	3.381e+000	5.4
3.595e+000	3.566e+000	0.8

Los cálculos se realizaron en un equipo PC-450 (128 MB de RAM).

Ejemplo 3

Se tiene en cuenta una pletina cuadrada fina con una matriz de masas coherente sujeta a lo largo de un borde. Se utiliza el elemento de lámina de 4 nudos y la malla 128x128 (el número de ecuaciones Neq es de 99 072). Se extraen los 40 pseudomodos.

En la tabla D5, se presentan el tiempo de cálculo y el espacio de almacenamiento en disco de los métodos de Lanczos (Skyline y Sparse), de Lanczos modificado (solvente iterativo) y de gradiente de Ritz (PCG_Ritz).

Tabla D5. Requisitos de tiempo de cálculo y almacenamiento en disco para varios métodos.

Método	Tiempo (s)	Disco duro (MB)
Lanczos, solvente Skyline	141 559	7 367
Lanczos, solvente Sparse	15 615	157
Lanczos modificado, solvente iterativo	18 978	0 en el núcleo
PSG_Ritz	9 651	192

Los cálculos se realizaron en un equipo PC-450 (128 MB de RAM).

Las diez primeras frecuencias obtenidas por Lanczos (Skyline o Sparse) y Lanczos modificado (solvente iterativo, preacondicionamiento ICCF, 3 niveles de agregación, 8 iteraciones interiores y tolerancia 1.0e-03 para la generación de vectores de Lanczos) son idénticas. Como la precisión de los cálculos era muy alta, era posible considerar que esos valores eran exactos dentro del modelo discreto especificado. Se han adoptado como valores de etalon para la estimación de errores de las frecuencias obtenidas mediante el método PCG_Ritz. Se ha seleccionado el enfoque multinivel con preacondicionamiento ICCF (1 nivel de agregación 4 iteraciones internas) cuando se ha aplicado el método PCG_Ritz. Los resultados correspondientes se presentan en el cuadro D6.

Tabla D6. Comparación de frecuencias de los métodos PCG_Ritz y de Lanczos

Frecuencias por Lanczos (Hz)	Precisión	Frecuencias por PCG_Ritz (Hz)	Error (%)
3.722e+000	5.918e-014	3.725e+000	0.08
9.112e+000	4.474e-014	9.115e+000	0.03
2.282e+001	2.424e-012	2.284e+001	0.09
2.915e+001	5.866e-013	2.915e+001	0.00
3.315e+001	1.795e-013	3.318e+001	0.09
5.801e+001	2.373e-011	5.803e+001	0.03
6.565e+001	3.028e-011	6.571e+001	0.09
6.873e+001	6.907e-014	6.875e+001	0.03
7.602e+001	1.549e-012	7.609e+001	0.09
9.949e+001	3.302e-013	9.953e+001	0.04

Ejemplo 4

El edificio grande se presenta en la fig. D3.

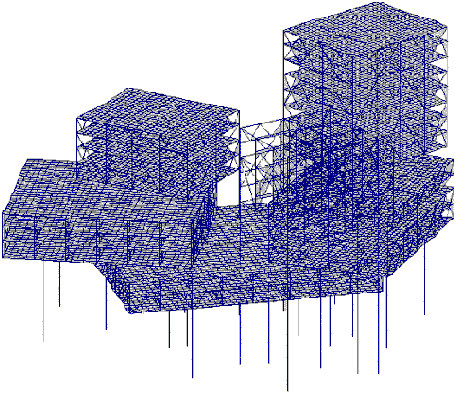
Fig. D3. Edificio grande. Número de nudos: 26 126. Número de elementos: 30 272.

Número de ecuaciones: 155 920.

Se tienen en cuenta el análisis estático lineal (un único caso de carga) y la extracción de 10 modos propios. La tolerancia adoptada para el solvente iterativo es igual a 1.0e-04. Para el solvente Skyline, se utiliza el método de Lanczos. Para el solvente Sparse Direct, se aplican los métodos de Lanczos y BLSI. El método de Lanczos modificado se utiliza para el solvente iterativo (método de varios niveles con 3 niveles de agregación, 4 iteraciones internas y preacondicionamiento ICCF). Tipo de matriz de masas: concentrada con rotaciones.

Tabla D7. Tiempo de cálculo y espacio en disco de varios métodos

Método	Espacio en disco (MB)	Estático lineal (único rhs) (s)	Extracción de 10 modos propios (s)	Tiempo total (s)
Skyline	5 702	136 065	65 052	203 878
AEBEIS	52	2 442	25 793	28 355
Sparse (método de Lanczos)	773	10 253	24 500	35 762
Sparse NS (método BLSI)	773	10 253	11 534	22 604

Los cálculos se realizaron en un equipo PC-450 (128 MB de RAM).

Conclusiones

Los métodos avanzados BLSI y de Lanczos basado en el solvente Sparse Direct y el solvente iterativo de alto rendimiento AEBEIS con preacondicionamiento ICCF son herramientas eficaces para la solución de problemas lineales estáticos y de valores propios a gran escala. Reducen considerablemente el tiempo de cálculo y los requisitos de almacenamiento en disco en comparación con un solvente Skyline convencional. El método de gradiente de Ritz (PCG_Ritz) es un enfoque rápido que permite estimar el comportamiento sísmico de la estructura especificada. Si se acepta un único nivel de agregación, los resultados correspondientes, obtenidos por el método PCG_Ritz, se aproximan a los obtenidos por el método de Lanczos o BLSI.

Referencias

1. E.L.Wilson. An eigensolution strategy for large systems. Computers&Structures, Vol. 16, N.º 1-4, pág. 259 - 265, 1983.
2. Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21 - 23, North-Holland.
3. E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, California, EE. UU., 1996.
4. R.W.Clough, J.Penzien. Dynamics of Structures. McGraw-Hill Book Comp., 1975, pág. 634
5. Fialko S. Yu. Investigaciones sobre la influencia de las imperfecciones iniciales en las vibraciones naturales de las láminas cónicas corrugadas, Mecánica soviética aplicada, 1982, 18, N11, pág. 118 - 122 (en ruso).
6. Fialko S. Yu. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, vol. 23, N6, pág. 547 - 552.
7. Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. Pág. 193-207.
8. Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics - engineering sciences), IV, 2000
9. Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
10. Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
11. Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
12. Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
13. S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, pág. 75-104.
14. Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics (Conferencia sobre los efectos de la carga transitoria rápida en el contexto de la mecánica estructural), Lausana, Suiza, 26 y 27 de agosto de 1987.
15. Hughes T.J.R., R.M.Ferencz y j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
16. Hughes Th. J. R. "The Finite Element Method. Linear Static and Dynamic. FEM Analysis".
17. Parlett B.N., 1980. "The Symmetric Eigenvalue Problem". Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
18. Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 - 471, 1997.
19. Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829 - 840, 1994.
20. Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529 - 3544, 1995.
21. Guía normativa
22. I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Oscilaciones de láminas corrugadas de revolución, Kiev, Naukova Dumka, 1988, pág. 169 (en ruso).
23. S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, vol. 20, N11, pág. 1033-1037 (en inglés).