定義の必要がある粘性構成関係の最後の部分は、スカラー損傷変数 D の進展用の方程式です。

損傷の進展モデルは、粘性材料によって保持された結合荷重の正確な履歴に関係なく、0 (ゼロ)の初期値から 1 の最終値に至るまで、損傷変数 D の進展を正確に表現できなければなりません。損傷の進展モデルの開発は、ひずみ(つまり、相対変位)、または応力で表現できますが、この最初の導入ではひずみに基づく(相対変位)方法を採用しています。損傷の進展は、法線方向およびせん断相対変位から異なる影響を受けると論理的かつおそらく直感的に仮定できます。しかし、ここでは簡素化するために、損傷の進展は、相対変位(有効な相対変位 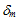と呼ばれる)の 1 つのスカラー測定の関数として表現できると仮定します。

対応する有効な表面力は、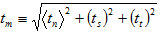 として定義されます。

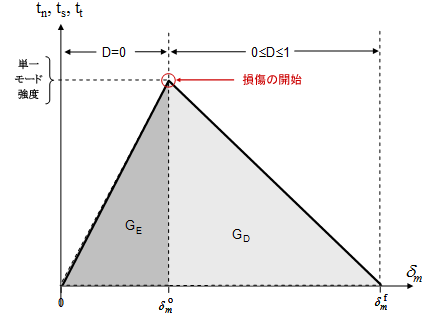
上図では、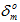 は次の場合など損傷の開始時での有効な相対変位値 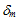を示します。たとえば、

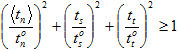
を満たす場合などです。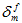 は、材料の剛性が完全にゼロにまで劣化した時の有効な相対変位値 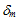を示します。 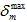は、現在の時間以下の任意の時間 t に対して、現在までに材料が到達した有効な相対変位 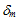の最大値を表します。 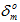および 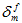は、材料特性の一部と見なされることに注意してください。

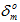
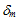
範囲 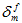内の任意の 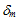値に対して、損傷変数 D の現在の値は、次の損傷の進展の方程式で表すことができます。

Helius PFA で提供される 3 つの粘性構成モデルの主な違いは、損傷の進展を評価する目的で 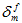が計算される正確な方法に関連します。全変位モデルでは、 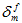の値は、ユーザ指定のパラメータ( 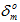- 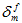)に損傷の開始時 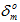の有効な相対変位を単に追加することにより計算されます。よって、損傷の開始が発生し、 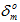が判明している場合、完全な材料劣化時(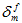)の有効な相対変位は、粘性材料の結合荷重状態が変化した場合でも固定したままになります。

総エネルギー モデルまたは混合モードべき乗則での 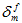の計算方法を理解するには、まず、いくつかのエネルギー式を定義する必要があります。任意の時点における、法線方向およびせん断変形に関連付けられた個別のエネルギー成分は、次のように定義します。

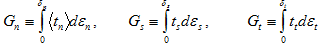
粘性材料によって吸収される総エネルギーは、単に 3 つのエネルギー成分の合計です。

Gtotal = Gn + Gs + Gt

総エネルギー Gtotal が臨界総エネルギー値 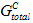に達すると、粘性材料は完全にゼロの剛性にまで劣化し、いかなる荷重も支持できなくなります。よって、臨界総エネルギー値 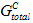を把握することで、次に示すように粘性材料が完全な劣化に達したときの有効な相対変位 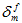を計算できます。

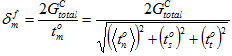
総エネルギー モデルでは、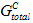 は変化しません。粘性材料に適用される表面力の瞬間的な混合に関係なく、同じユーザ指定の定数となります。混合モードべき乗則については、 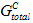の値は、粘性材料に作用する表面力成分の変化する混合に反応して継続的に変化します。混合モードべき乗則では、 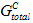の瞬間的な値は、次の条件が満たされるまで Gn、Gs、Gt の瞬間的な値を均一に上方に調整することで取得できます。

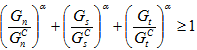
瞬間的な表面力のセット(tn、ts、tt)、および瞬間的な個々のエネルギー密度成分(Gn、Gs、Gt)が与えられると、上記の基準を使用して、基準が満たされるレベルまでこれらの表面力を均一に調整できます。この調整された表面力を()、その対応する調整されたエネルギー成分を(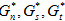)として示します。はく離の伝搬という結果になる投影されたエネルギー成分(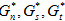)を仮定して、はく離の伝搬という結果になる総エネルギーを として計算できるようになります。