エネルギー ベースの損傷進展の紹介

公式化されたエネルギー ベースの損傷進展を表示します。

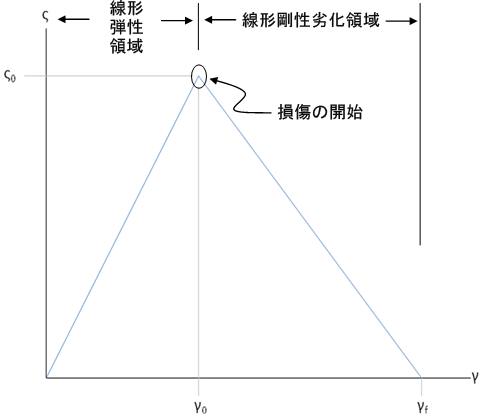
材料劣化の速度を制御可能にする最も簡単で実現可能な構成関係は、線形弾性領域とそれに続く線形剛性劣化領域からなるバイリニアの法則です。この図では、ς0 は破損の開始時点の複合応力の有効な値を表します。 γ0 は破損の開始時点の複合ひずみの有効な値を表します。 γf は、損傷が完全に進展し、材料の剛性が 0 まで完全に劣化し、材料に荷重を適用できない状態になったときの複合ひずみの有効な値を表します。

ここで、体積が Ve の完全に劣化した要素によって散逸されたエネルギーの合計 G を考えます。 上の単純な構成関係では、合計散逸エネルギーは、次の式により表すことができます。

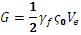
ここで、γf は測定された有効なひずみの最終的な値で、ς0 は破損の開始時に測定された有効な応力の値です。

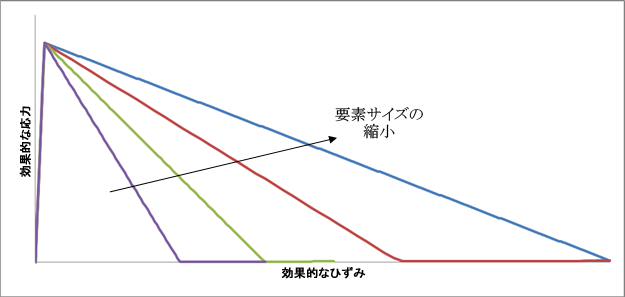
進行性破損の結果に関連付けられるメッシュの感度を緩和する鍵は、要素の大きさに関わらず、散逸エネルギーの合計を一定に保つことです。この一定のエネルギー散逸は、ς0 または γf を要素の大きさの関数として適切に制御することで得ることができます。 破損解析の目的で、ς0 の値を変更すると、複合材料の破損を引き起こすと言われている応力を効果的に変更することができます。 これは、あまり魅力的な方法でないことがすぐにわかります。ここで取るべき最も自然な方法は、次のように γf の値を変更して、変化する要素の大きさに対してエネルギー G を維持するようにすることです。

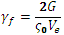
次の図は、要素の大きさが変化したときの、許容される単一のGの値に対して得られる構成則のまとまりを示します。