非線形弾性繊維

一方向複合材料が大きな繊維方向の軸ひずみを受けている場合、非線形性弾性が発生する傾向があります。

非線形弾性は、主に複合材料の E 11 に影響を与え、繊維の結晶配列に起因する場合があります[21]。結晶が縦方向引張に沿ってもっと整列すると、剛性が高くなります。繊維の圧縮で結晶の方向が定まらなくなると反対の現象が発生し、剛性が低くなります。繊維が引張で荷重されると、Helius PFA では Murphey およびその他によって提案された一次モデルを使用し[21]、セカント係数を使用するために繊維の係数を変更します(方程式 28).

ここで、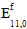 は元の繊維の係数、 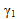は非線形パラメータ、 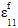は複合材料の軸ひずみと等しいと仮定される繊維の軸ひずみです。複合則を使用して、更新された繊維の係数に基づいて複合材料の係数を計算します(方程式 29).

ここで、φi は、繊維(i=f)および母材(i=m)の体積分率を示します。 その他のすべての繊維および複合材料の弾性定数は元の値を保持します。

軟化動作をモデル化するために圧縮下の繊維の係数を変更する場合に 2 つのオプションが存在します。方程式 28 を異なる非線形パラメータ(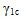)で使用できます。または、複合材料の係数のノックダウン ファクター ηc を使用して、方程式 30 に示すように、軟化動作をシミュレーションできます。

ここで、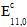 は元の複合材料の係数です。その他のすべての繊維および複合材料の弾性定数は元の値を保持します。

方程式 31 は、圧縮非線形パラメータ(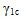)の値における制限で、破損の発生前に係数がゼロになるのを防止します。

ここで、C1 は縦方向の圧縮強度の絶対値です。

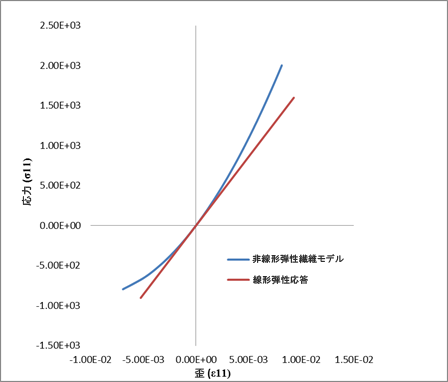
次のプロットは、異なる非線形のパラメータ(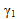 および ηc)を使用して、純粋な軸荷重下での材料における複合材料レベルの応力-ひずみ動作を比較したものです。黒い破線は、非線形弾性繊維モデルが有効でない場合に使用される線形弾性応答を表します。

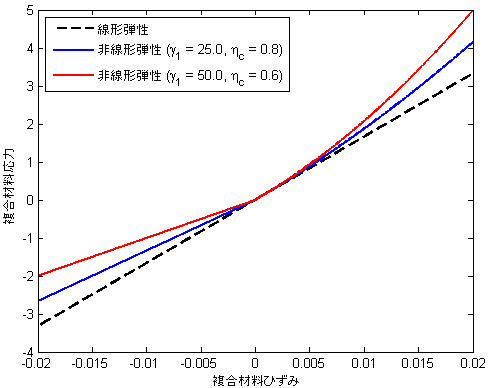
次のプロットは、圧縮と引張の方程式 28 で指定したモデルを使用して、縦方向の応力-ひずみ応答を比較したものです。