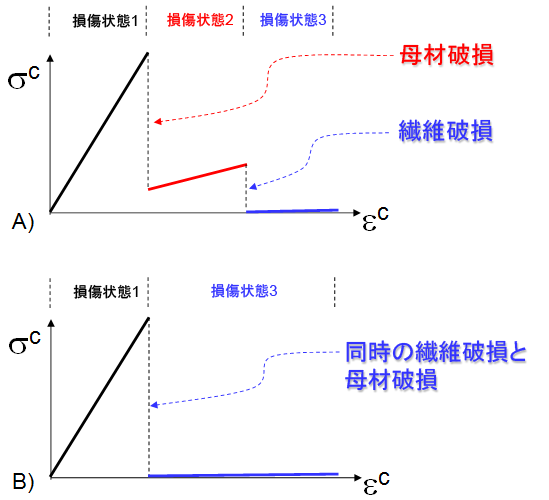
一方向複合材料の損傷状態
一方向複合材料には、3 つの複合材料損傷状態があります。
損傷状態 1: 破損していない母材構成と破損していない繊維構成
損傷状態 2: 破損した母材構成と破損していない繊維構成
損傷状態 3: 破損した母材構成と破損した繊維構成
4 番目の複合材料損傷状態、つまり破損していない母材構成と破損した繊維構成の組み合わせが可能であるという主張もあるでしょう。しかし、ほとんどの強化繊維複合材料では、母材破損を発生させずに繊維破損のみを引き起こす荷重セットを適用するのは事実上不可能です。したがって、複合材料に適用される結合荷重の正確なフォームに関係なく、荷重の大きさが安定して増加することで、複合材料 CIR の損傷状態に対し、次の 2 つの起こり得る履歴のいずれかになることが仮定されます。
履歴 1: 損傷状態 1 → 損傷状態 2 → 損傷状態 3
履歴 2: 損傷状態 1 → 損傷状態 3
下図は、これら 2 つの履歴の定性的性質を示しています。次に示す複合材料の全体的な応答に関して、いくつかの問題をさらに掘り下げてみましょう。第 1 に、複合材料の 3 つの異なる各損傷状態に対して、複合材料の剛性および熱特性(Cc および αc)を、破損または破損なしの状態を持つ構成材料を含むミクロ構造の均質化により取得します。ミクロ構造内の破損した母材構成では、母材構成の剛性は、元の母材剛性 CIR のユーザ指定のパーセンテージ(既定=10%)まで等方的に低減します。 低減した母材剛性は、均質化プロセスを通じて、複合材料の剛性に直接影響します。ミクロ構造内の破損した繊維構成では、繊維構成の剛性は、元の母材剛性 CIR のユーザ指定のパーセンテージ(既定=1%)まで等方的に低減します。 低減した繊維剛性は、均質化プロセスを通じて、複合材料の剛性に直接影響します
第 2 に、下記に示す 3 つの複合材料の各損傷状態に対して、個別の MCT 分解を定式化する必要があります。MCT 分解は線形構成関係を使用する必要があり、Cc、Cf、Cm、αc、αf、αm の個別の成分は単に定数であることを思い出してください。一般的に、これらの定数は、応答の 1 つの線形セグメントと次のセグメントで異なります。よって、MCT 分解のセクションごとに異なります。3 つの異なる損傷状態に対して複合材料の全体的な応答を制限することで、応答の各セグメントに対して必要な MCT 分解係数を決定するプロセスは、一度に実行することができます。結果の定数はデータベースに格納されます。次に、複合材料の個別の損傷状態に応じて、MCT 分解定数の適切なセットをデータベースから簡単に取得できます。この機能により、Helius PFA の全体的な計算効率が著しく向上しています。
最後に、大規模な複合材料構造の進行性破損解析では、非常に離散的な材料応答(下記を参照)を使用しても、複合材料構造全体として非常に離散的な応答は生成されないことに注意する必要があります。実際には、予測される複合材料構造全体の進行性破損応答は、最終的な破損荷重に至るまでかなりスムーズである場合が多いです。この直感的ではない結果の理由は、個別の材料応答(下記を参照)は構造全体に分散する数千(または数百万)の異なるガウス積分点に個別に適用されるためです。応力レベルが構造内の点間で異なるならば、複合材料構造の特定の荷重増分中に、これらのガウス積分点のうち、非常に小さいパーセンテージでのみ破損が生じることを予測できます。このため、非常に不連続な構成関係を使用しても、構造の応答はスムーズなものになります。