複合材料の疲労解析プロセスの最終的な手順は、接着破壊率を複合材料の巨視的な破損にリンクすることです。

損傷の進展パラメータ

前述したとおり、Hansen と Baker-Jarvis [36]は、損傷パラメータ n を導入することによって KTF と巨視的な損傷をリンクしました。このパラメータは、破損時の微小亀裂密度に対する微小亀裂密度のパーセンテージを示します。この損傷変数は、破断に必要な微小亀裂密度の割合を表し、初期値はゼロで破損時の値は 1 です。その定式化において、時間 t を用いる損傷の進展変数 n の微分方程式を導入しています。ここで、損傷の進展変数は接着破壊率に直接関連付けられています。この方法では、広範な応力速度の影響を受ける樹脂の強度を適切に予測しました。

Hansen と Baker-Jarvis により提案された式と非常に類似した、n の進展を説明する微分方程式が使用されています。

n 0 は条件を強制することで決定されるパラメータであり、

ni は疲労荷重開始時の損傷値です。この定式化と Hansen と Baker-Jarvis の式との違いは、後者の定式化では λ=1 と仮定する点です。この値は、現在の実装で使用される既定値です 2。λ=1 の場合、

λ の値が 1.0 であると仮定して、方程式 57、52、56 を結合することで、樹脂の疲労寿命を決定するための開始方程式となります。

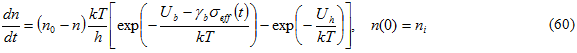
方程式 61 を解くと時間を用いた損傷の進展パラメータを得ることができます。この方程式は次のように記述できます 3。

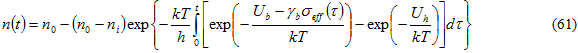
方程式 61 は校正値 Ub、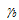、Uh と使用でき、損傷パラメータの値が 1 になる(n = 1)時間を決定します。

2 単一の線形弾性解析、つまり進行性破損がない場合は、λ の選択は関係ありません。 λ のすべての解は、同じ破損までのサイクル数を生成します。ただし、この係数はブロック荷重および進行性破損シミュレーションでは重要となる場合があります。

3 方程式 61 の定式化で U および T が疲労プロセス中で一定であると仮定することを想定しています。