2 つの構成(繊維/母材)複合材料の関係を作成します。

構造レベル解析では、複合材料構造内の任意の材料点における複合材料の平均応力とひずみ状態(σc および εc)に直接アクセスできます。このセクションでは、εc を構成の平均応力とひずみ状態(σf、εf、σm、εm)に分解できる 2 つの構成(繊維/母材)複合材料の関係を作成します。この MCT 分解のフレームワークは、前のセクションの方程式 4 と 8 により提供され、あらゆる材料応答とすべてのレベルの変形に対して有効です。

MCT 分解作成の最初の手順は、対応する平均ひずみ測定値に関連して平均応力測定値を表現する、適切な構成関係を呼び出すことです。MCT 分解を固有で数学的に扱いやすい状態に保つため、構成関係は線形であるという制限を課しています。後で説明しますが、線形構成関係への制限は深刻な制限をもたらすものではありません。MCT 分解は非線形問題でも利用することがでます。方程式 12～14 は、使用されるさまざまな体積平均化および線形化された構成関係をリストしています。

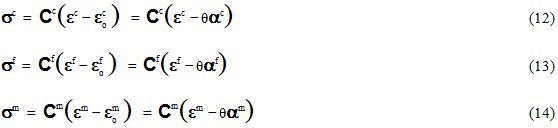
方程式 12 ～ 14 では、Cc、Cf および Cm は、均質化された複合材料、繊維構成、および母材構成材料の 6 行 6 列の構成行列(セカントの定式化)をそれぞれ表します。θ は、材料特性が測定された均一な参照温度に対する複合材料の均一な温度変化を表します。項 αc、αf、αm は、均質化された複合材料、繊維構成、および母材構成材料の線膨張係数をそれぞれ表す 6 行 1 列の ベクトルです。構成関係は線形であるため、個別の成分、Cc、Cf、Cm、αc、αf、αm は単に定数です。しかし、MCT 分解を非線形問題に適用するには、構成関係(方程式 12 ～ 14)は、現在の状態に関して線形化されると仮定します(σc、εc、σf、εf、σm、εm、θ で定義)。このアプローチは、非線形構造レベル解析で一般的に使用される方法と完全に一致しており、複合材料構造の全体的な非線形応答が区分線形応答シーケンスによって表現されます。

次に、線形化された構成関係(方程式 12 ～ 14)を方程式 4 に代入し、次の方程式を生成します。

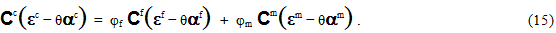
さらに、方程式 8 を方程式 15 に代入し、次の方程式を生成します。

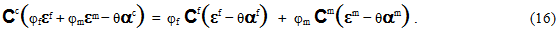
方程式 16 は、同様の項をグループ化して、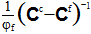 ですべての項を乗算することで、繊維平均ひずみ状態(εf)を計算できるようになり、次の方程式を生成します。

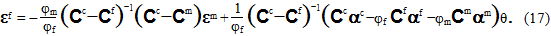
この時点で、以前に課した線形構成関係の制限の利点をよく理解することができます。具体的には、Cc、Cf、Cm、αc、αf、αm の成分が定数でなければ、方程式 17 を生成する代数が処理が困難になります。

便宜上、6 行 6 列の行列 A と 6 行 1 列のベクトル a を次のように定義します。

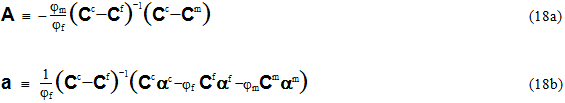
これらの新たに定義した数量を使用して、方程式 17 は次のように簡単に記述できます。

行列 A は構成の平均機械的ひずみに関連しているのに対し、ベクトル a は構成の平均熱ひずみに関連しています。方程式 19 は方程式 8 から平均繊維ひずみ εf を削除するために使用できます。これは、複合材料の平均ひずみ状態 εc に対する母材の平均ひずみ状態 εm を表現します。

母材の平均ひずみ状態 εm が方程式 20 によって計算されたら、繊維の平均ひずみ状態 εf は単に 方程式 8 を使用して次にように計算できます。

母材と繊維の平均ひずみ状態(εm および εf)両方を計算した後、母材と繊維の平均応力状態(σm および σf)を線形化された構成関係を使用して計算できます(方程式 13 および 14)。

要約すると、MCT 分解の解析フォームは 4 つの方程式(方程式 20、21、13、14)で構成されます。これらの方程式は、任意の材料点の複合材料の平均ひずみ状態を、同じ材料点の構成の平均ひずみと応力状態に分解するために使用します。この分解は、複合材料の平均ひずみ状態が判明している複合材料構造内の任意の点で非常に効率的に実行できます。MCT 分解は、異種複合材料のミクロ構造の状態に関する物理的理解を向上できるテクノロジーです。後で説明しますが、構成の平均応力とひずみ状態の情報から得られる主な利点は、複合材料のミクロ構造内の構成の損傷の進展と材料破損の予測を可能とする物理的根拠が改善されることです。

MCT 分解の基礎となる方程式は、方程式 20 で提供されます。方程式 20 は、複合材料の平均ひずみ状態 εc を母材の平均ひずみ状態 εm にマッピングする伝達関数とみなすことができます。非線形応答を示す複合材料に方程式 20 を使用する意味を説明することが有益となります。最初に、εc の εm へのマッピングは、完全に数量 Cc、Cf、Cm、αc、αf、αm、φf、φm (ぞれぞれが定数であると仮定)によって定義されます。したがって、非線形材料応答または有限変形に対して、構成関係(方程式 12 ～ 14)を現在の状態に関して線形化する必要があります(σc、εc、σf、εf、σm、εm、θ で定義)。この制限は、複合材料の全体的な非線形応答を線形応答の有限シーケンスで表現する必要があることを意味します。ここで Cc、Cf、Cm、αc、αf、αm は応答の各セグメント内の定数と見なすことができます。実際には、MCT 分解は応答の各セグメントで異なります。これは Cc、Cf、Cm、αc、αf、αm がセグメント間で変化するためです。上述したとおり、材料応答の区分線形表現は、非線形構造レベル解析で一般的に使用される方法と完全に一致しています。

また、MCT 分解(まとめて方程式 20、21、13、14)は、最小の計算処理量を必要とすることにも留意してください。したがって、合計の計算時間を大幅に増加させることなく、構造レベル解析で懸念するすべての点に適用することができます。たとえば、複合材料構造の構造レベルの有限要素解析で、モデル内の各ガウス積分点で MCT 分解を使用した場合、通常、合計解析時間は 2%～3% だけ長くなります。

解析の 2 分割化は、特に単純な一方向繊維強化複合材料で効果的です。Helius PFA はすべての一方向強化複合材料に対して、解析の 2 分割化を使用します。織物複合材料または組物複合材料でも、けん引平均応力とひずみから、繊維および母材の平均応力とひずみへの最終的な分解は、解析の 2 分割化を使用して実行します。